ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ

ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ

ВЫСШЕГО ОБРАЗОВАНИЯ

СТАВРОПОЛЬСКИЙ ГОСУДАРСТВЕННЫЙ АГРАРНЫЙ УНИВЕРСИТЕТ

Кафедра информационных систем

РАСЧЕТНАЯ РАБОТА

ПО ДИСЦИПЛИНЕ

«ИНФОРМАЦИОННЫЕ КОМПЬЮТЕРНЫЕ ТЕХНОЛОГИИ»

Вариант № 25, 15, 15

Выполнила: студентка 12 группы 1 курса

Рябцева Виктория Владимировна

Факультет: Агробиологии и земельных ресурсов

Направление: 21.04.02- Землеустройство и кадастры

магистр по программе Территориальное планирование и землеустройство

Проверила: к.э.н., доцент Кузьменко И.П.

Ставрополь, 2016

Вариант №25

Решить задачи методом линейного программирования

Задача №1- найти максимум

F(x) = 3 + 10 → max

+ ≤ 300

2 + 10 ≤ 2200

1. Превращаем неравенство в равенство, т.е. добавляем и .

+ + = 300

2 + 10 + = 2200

F(x) = 3 + 10 → max

2. В системе ограничений нет переменных, которые входили бы в левую часть 1 раз и с положительным знаком, т.е. начальное опорное решение выделить не возможно, поэтому создаем искусственные переменные 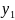и , а в целевой функции эти переменные умножаем на сколь угодно большое число m и добавляем и .

+ + + = 300

2 + 10 + + = 2200

F(x) = 3 + 10 +M ( + ) → max

3. Выделяем начальное опорное базисное решение с искусственным базисом.

+ + )

= 2200 - (2 + 10 + )

F(x) = 0 – (- 3 - 10 )

M [2500 – (3 + 11 + + )]

4. Наши значения переносим в таблицу 1.

базис				Q
	300	1	1	300	Rстр.
	2200	2	10	220
F(x)	0 2500	-3 3	-10 11	m + 1 m + 2

Rстб.

5. Выбираем в целевой строке наибольшее отрицательное значение по абсолютной величине. Это и будет разрешающий столбец.

6. Находим значение Q, которое рассчитывается по формуле

Q =

7. Выбираем наименьшее = 220 – является Rстр.

8. На пересечении строки и столбца находится разрешающий элемент , который говорит о том, что мы переносим в базис, а выбрасываем.

базис
	80
	220
F(x)	2200	-1	1

9. Таблицу 2 заполняем с помощью правил однократного замещения.

1) Заполняем клетку разреш. элемента по следующему правилу

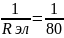
2) Заполняем разрешающий столбец с противополож. знаком.

3) Заполняем разрешающий строку с этим же знаком.

4) Все оставшиеся клетки заполняем по правилу прямоугольника.

10. Задача не решена, т.к. в функции цели имеются отрицательные значения которые принесут прибыль.

11. Переходим к таблице 3.

базис
	200
F(x)	2300

Ответ: Задача решена, т.к. в целевой функции отсутствуют отрицательные значения, которые принесут прибыль.

Ответ: = 100; = 200; = 0; = 0.

F(x) = 3*100+10 * 200= 2300.

Задача №2- найти минимум

F(x) = 3 + 4 → min

+ ≥ 6

2 + 5 ≥ 21

1. Приводим неравенство к канонической форме.

+ - = 6

2 + 5 - = 21

F(x) = 3 + 4 → min

2. В системе ограничений нет переменных, которые входили бы в левую часть 1 раз и с положительным знаком, т.е. начальное опорное решение выделить не возможно, поэтому создаем искусственные переменные и , а в целевой функции эти переменные умножаем на сколь угодно большое число m и добавляем и .

+ - + = 6

2 + 5 - + = 21

F(x) = 3 + 4 +M ( + ) → min

3. Выделяем начальное опорное базисное решение с искусственным базисом.

+ - )

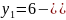= 21 - (2 + 5 - )

F(x) = 0 – (- 3 - 4 )

M [27 – (3 + 6 - - )]

4. Составляем начальную таблицу 1.

базис		x1	x2	x3	x4
x3	-6	-1	-1	1	0
x4	-21	-2	-5	0	1
F(X0)	0	3	4	0	0

Чтобы решить задачу необходимо переменные и перебросить вверх таблицы и назад в базис не возвращать.

Выбираем разрешающий столбец (R) по коэффициенту строки m + 2. Это тот элемент в котором наибольшее положительное значение . Выбираем разрешающую строку, используя и рассчитывая элемент Q = ;

На пересечении появляется разрешающий элемент.

Выбираем однократное замещение. переносим в базис, перемещаем в свободные элементы. Вторую и последнюю таблицы заполняем по 4 правилам заполнения таблиц.

базис		x1	x2	x3	x4
x4	9	3	0	-5	1
x2	6	1	1	-1	0
F(X1)	-24	-1	0	4	0

В задачах на min 1 и 2 правило не используется.

Заполняем разрешающую строку.

базис		x1	x2	x3	x4
x1	3	1	0	-12/3	1/3
x2	3	0	1	2/3	-1/3
F(X2)	-21	0	0	21/3	1/3

Оставшиеся клетки заполняем по правилу прямоугольника.

В строке m + 2 есть положительные числа, поэтому задача не решена. Переходим к таблице 3. Выбираем разрешающий столбец.

Ответ: в таблице 3 в строке m+2 находятся все 0. В строке m+1 нет отрицательных значений. Это является математическим критерием того, что задача решена и оптимальное решение найдено. = 3; = 3; = 0; = 0. F(x) = 3*3+4*3= 21.

Вариант №15

Рассчитать оптимальный план

Задача №3- Критерий – min

Задача распределительного типа на минимум функции.

Составляем начальные планы 3-мя способами.