Міністерство освіти і науки України

ОДЕСЬКА НАЦІОНАЛЬНА МОРСЬКА АКАДЕМІЯ

Кафедра фізики і хімії

Лабораторна робота № 3.2

ВИМУШЕНІ КОЛИВАННЯ

(Вказівки до лабораторної роботи)

Склав проф. Михайленко В.І.

Затверджено на засіданні кафедри 21 лютого 2009 р., протокол № 4   

Одеса – 2009

Лабораторна робота № 3.2

ВИМУШЕНІ КОЛИВАННЯ

1. ТЕОРЕТИЧНА ЧАСТИНА

1.1. ЗАГАЛЬНА ХАРАКТЕРИСТИКА КОЛИВАНЬ

Коливаннями називаються рухи або процеси, що характеризуються тим чи іншим ступенем повторюваності в часі.

Коливання називаються періодичними, якщо значення усіх фізичних величин, що характеризують коливальну систему, повторюються через рівні проміжки часу.

Час здійснення одного повного коливання називається періодом коливання – Т.

Частотою періодичних коливань називається величина  =1/Т, рівна числу повних коливань за одиницю часу. Одиниця виміру частоти –1 Герц –одне повне коливання за 1 секунду.

Циклічною частотою періодичних коливань називається величина =2=2/Т, рівна числу повних коливань за 2 секунд.

Періодичні коливання величини x(t) називаються гармонічними, якщо вона змінюється за законом синуса або косинуса.

Надалі ми будемо розглядати гармонічні коливання, що змінюються за законом косинуса

(1)

Тут _o – циклічна частота гармонічних коливань; -амплітуда коливань, тобто максимальне по модулю значення коливальної величини x; – фаза; – початкова фаза коливань.

Знаючи фазу коливань, можна визначити величину зміщення x у даний момент часу. Початкова фаза коливань показує величину зміщення від положення рівноваги в початковий момент часу, тобто при t=0:

1.2. Додавання гармонічних коливань однакового напрямку

Рис. 1.

Рішення ряду питань полегшується, якщо зображати коливання графічно у вигляді векторів на площині. Отримана в такий спосіб схема називається векторною діаграмою.

З точки О, узятої на осі x, проведемо вектор , що утворює з оссю x кут . Проекція цього вектора на вісь x дорівнює (рис.1):

Припустимо тепер, що вектор А рівномірно обертається з кутовою швидкістю _o. Тоді за час t він опише кут і його нова проекція на вісь х стане:

(2)

Отже, проекція кінця вектора на вісь буде виконувати гармонічні коливання з амплітудою, рівній довжині вектора А, з частотою ₀ , рівною кутовій швидкості обертання вектора, і з початковою фазою ₀, рівною куту, утвореному вектором А з віссю х у початковий момент часу.

Розглянемо додавання двох гармонічних коливань однакового напрямку й однакової частоти:

Рис. 2.

Представимо обидва коливання за допомогою векторів А₁ і А₂, що утворюють з оссю х кути і відповідно (рис. 2). Побудуємо за правилом додавання векторів результуючий вектор А_р. З рис. 2 видно, що проекція цього вектора на вісь х дорівнює сумі:

Вектор А_р обертається з тією же кутовою швидкістю _o, що і вектори А₁ і А₂, отже результуюче коливання буде гармонічним з частотою _o, амплітудою А_р і початковою фазою :

Знайдемо тепер з векторної діаграми (див. рис. 2) результуючу амплітуду А_р. З заштрихованого трикутника за теоремою косинусів маємо:

(3)

1.3. Вимушені коливання

У реальних умовах коливальна система поступово втрачає енергію на подолання сил тертя. У результаті, коливання є загасаючими. Щоб коливання були незагасаючими, необхідно якимсь чином підводити до коливальної системи енергію, поповнюючи її втрати.

Припустимо, що на коливальну систему діє зовнішня (вимушуюча) сила, що змінюється за гармонічним законом:

,

(4)

де  – циклічна частота, а – амплітудне значення сили.

Для наочності будемо вважати, що коливальна система уявляє собою пружинний маятник, що виконує коливання у в’язкому середовищі (рис. 3). Тоді на закріплене до пружини тіло буде діяти завертаюча сила, яка по своїй природі є пружною силою F_пр, і сила опору F_опору. За законом Гука

,

де x – зміщення від положення рівноваги (абсолютна деформація), а k – квазипружна постійна (у даному випадку жорсткість пружини).

При малих швидкостях сила опору пропорційна швидкості

,

(5)

де r – коефіцієнт опору, що залежить від форми тіла і в'язкості середовища.

Таким чином, результуюча сила, що діє на тіло, дорівнює сумі квазіпружної силі, силі опору та змушуючої силі:

.

Складемо рівняння руху, використовуючи другий закон Ньютона (F=ma):

.

Приймаючи до уваги, що a=d²x/dt², v=dx/dt, поділивши рівняння на масу m і позначивши r/m = 2 ( – коефіцієнт загасання); (_o – власна частота незагасаючих коливань), одержимо диференціальне рівняння вимушених коливань:

.

(6)

Розв’язок цього рівняння будемо шукати у вигляді:

,

(7)

тобто ми припускаємо, що система виконує коливання з частотою, рівній частоті коливань зовнішньої сили.

Для знаходження амплітуди А вимушених коливань продиференцюємо (7) двічі за часом і підставимо в (6). Маємо

,	(8)
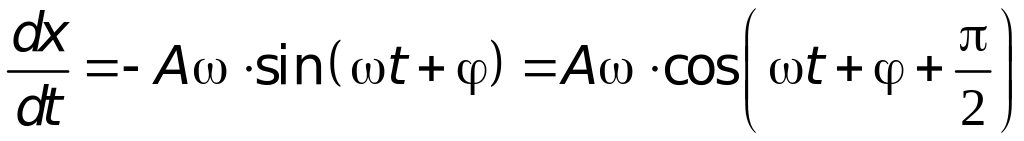
	(9)

Підставляючи (7–9) у (6), одержимо:

або

(10)

З виразу (10) видно, що в результаті додавання двох гармонічних коливань, зсунутих по фазі на /2, одержується гармонічне коливання з амплітудою F_o/m і початковою фазою, рівною нулю. При додаванні двох гармонічних коливань однакової частоти й однакового напрямку результуюча амплітуда коливань може бути знайдена за формулою (3). У даному випадку

Підставляючи ці вирази у формулу (3), одержимо:

(11)

Звідси

.

(12)

З виразу (12) видно, що амплітуда вимушених коливань залежить від частоти зовнішньої періодично діючої сили. При 0 АF_o/m_o; якщо ж , то А0. Графік залежності А від  при двох різних коефіцієнтах загасання представлений на рис. 4. При деякім значенні =_р амплітуда вимушених коливань досягає максимального значення. Явище різкого зростання амплітуди вимушених коливань, коли частота зовнішньої періодично діючої сили наближається до _р, називається резонансом. Частота _р, при якій настає резонанс, називається резонансною. Значення _р можна знайти з умови, що при =_p амплітуда A(_p)=max. Ця умова виконується, якщо підкореневий вираз в (12) при  =_р буде мінімальним. Це означає, що перша похідна за частотою від підкореневого виразу дорівнює нулю:

.

Звідси після нескладних перетворень знаходимо:

.

(13)

Резонансне значення амплітуди одержимо, якщо підставити (13) у (12):

Рис. 3.

. (14)

Видно, що чим менше коефіцієнт за­гасання , тим більше А_рез (рис. 3). У ряді випадків резонанс може стати небез­печним явищем, що спричинює за собою руйнування коливальної системи, внаслі­док надмірного зростання амплітуди.