2. Теоремы Силова

Определение 2.2.1.

1. Пусть 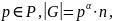где Подгруппа группы называется силовской -подгруппой группы ( -силовской, силовой), если и обозначается .

2. множество всех силовских подгрупп группы (множество всех силовских -подгрупп группы ).

Теорема 2.2.1 (Первая теорема Силова). Пусть

Тогда в существуют силовские -подгруппы.

Доказательство. Пусть – контрпример минимального порядка.

Расcмотрим

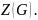
1. Пусть .

По лемме 1.2.2(2) . Так как .

Если то . Пусть . Противоречие.

2. Пусть не делится на . Рассмотрим формулу классов для

не делится на Таким образом, Тогда по лемме 1.2.3(2) не делится на . Следовательно, по теореме Лагранжа не делится на . Соответственно где

Допустим, что 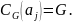Тогда Противоречие. Следовательно, Тогда .

Таким образом, Противоречие.

Из а) и б) вытекает, что контрпримера не существует. Следовательно, утверждение верно для любой . Теорема доказана.

Теорема 2.2.2 (Вторая теорема Силова). Всякая р-подгруппа группы содержится в некоторой силовской -подгруппе группы

Доказательство. Пусть ‒ р-подгруппа группы . Тогда , . Если β=0 ⇒ .

Если α=β ⇒ . Пусть . Пусть . Рассмотрим разложение в двойные смежные классы по подгруппе и :

Следовательно, Таким образом, такое что не делится на Соответственно , причем из . Теорема доказана.

Теорема 2.2.3 (Третья теорема Силова). Любые 2 силовские -подгруппы группы сопряжены в

Доказательство. Пусть и ‒ силовские -подгруппы группы . Покажем, что и сопряжены в . Так как ‒ -подгруппа группы , следовательно, по теореме 2.2.2 для некоторого и сопряжены в . Теорема доказана.

Теорема 2.2.4 (Четвертая теорема Силова). Число силовских р-подгрупп группы сравнимо с единицей по модулю и делит

Доказательство. Пусть ‒ число силовских р-подгрупп группы . Пусть ‒ силовская р-подгруппа группы . Тогда, по теореме 2.2.3, множество всех силовских р-подгрупп имеет вид:

⇒ .

Следовательно, Из (1) ⇒

Рассмотрим разложение в двойные смежные классы по подгруппе и :

. Соответственно, По формуле (2) ⇒ 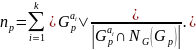Пусть . Тогда Покажем, что . Допустим, что не делится на . Тогда , такое что

. Таким образом, и ‒ два разложения силовских р-подгрупп в . С другой стороны, . Следовательно, ‒ единственная силовская р-подгруппа в , что является противоречием. Таким образом, ⇒ ⇒ . Теорема доказана.

3. Свойства силовских подгрупп

Лемма 2.3.1 (Фраттини). Пусть

Тогда

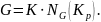
Доказательство.

1. Так как и то .

2. Покажем, что . Пусть

Рассмотрим сопряжены в Следовательно, Тогда Таким образом, Соответственно, . Следовательно, .

Из 1) и 2) получим Лемма доказана.

Лемма 2.3.2 Пусть Тогда

Доказательство. Пусть Покажем, что

1. С одной стороны

2. Покажем, что Пусть . Покажем, что .

Рассмотрим :

Таким образом, сопряжены в Следовательно, Тогда Таким образом, Лемма доказана.

Теорема 2.3.1 Пусть Тогда справедливы следующие утверждения:

1)

2)

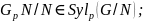
3)