2 Расчетное задание

2.1 Исходные данные

Исходные данные для варианта № 2 приведены в таблице 2.1

Таблица 2.1 Параметры исходных данных

0, см.	0+r0, см.	d1>>R1,см	d2 R1, см	d3<< R1,см	L
0,9	199,5	14	6,63	0,48	10 R1

2.2 Расчет радиусов десяти зон Френеля

Рассчитаем по формуле 2.1, радиусы десяти зон Френеля, взяв из таблицы 2.1 все необходимые параметры

2.1

Занесем результаты расчетов в таблицу 2.2.

Таблица 2.2 Результаты расчетов зон Френеля

№ зоны (n)	1	2	3	4	5	6	7	8	9	10
Rn	6,7	9,5	11,6	13,4	15,0	16,4	17,7	19,0	20,1	21,2
 x= Rn+1- Rn	-	2,8	2,1	1,8	1,6	1,4	1,3	1,3	1,1	1,1

2.3 Расчет продольного сечения существенной области

Рассчитаем и построим по формуле (2.1) продольное сечение области, существенной для распространения радиоволн, ограничив ее первой зоной Френеля. Заполним таблицу 2.3, изменяя ₀ от 0,2 до L см, и построим график зависимости R₁=f( ₀) (рисунок 2.3).

Рисунок 2.2 Продольное сечение области, существенной для распространения радиоволн

Таблица 2.3 Зависимость R₁ от ₀

№	1	2	3	4	5	6	7	8	9	10
r0, см	199,3	191,5	183,5	175,5	166,5	157,5	149,5	141,5	135,5	132,5
 0, см	0,2	8	16	24	33	42	50	58	64	67
R1, см	0,42	2,63	3,64	4,34	4,98	5,46	5,81	6,08	6,25	6,33

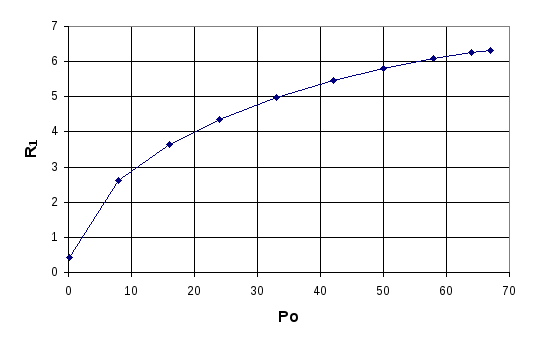
Рисунок 2.3 График зависимости R₁ от ₀

2.4 Положение плоскости установления экранов.

Определим положение плоскости установления экранов.

L/2= 10·R₁/2= 10ּ6,7/2=33,5 см

2.5 Зависимость f(u0) для дифракции на краю экрана

По формулам

, 2.3

, 2.4

где ,,

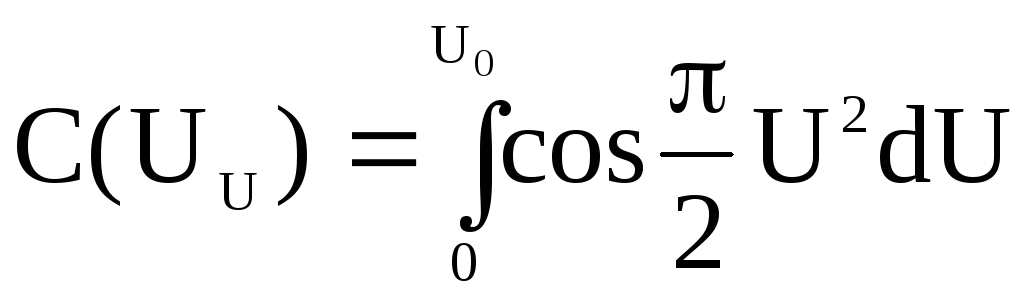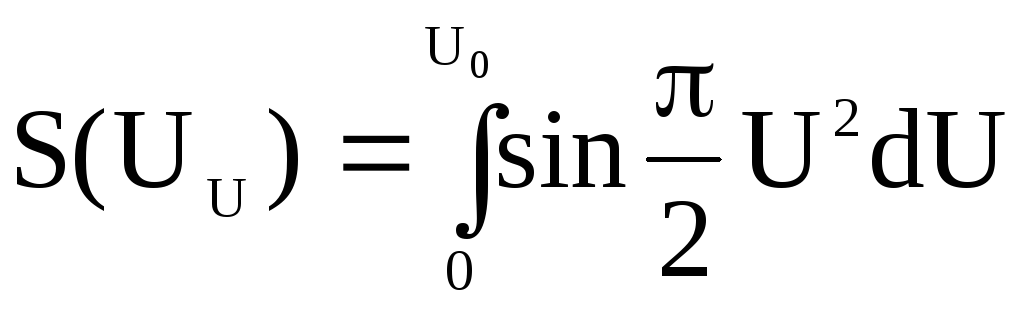рассчитаем зависимость F(U₀) для дифракции на краю экрана, изменяя U₀(х) от - R₁₀ до + R₁₀ см, для ₀ = r₀. График зависимости показан на рисунке 2.4.

Таблица 2.4 Расчетные данные

x0	U0	C(U0)	S(U0)	F(U0)
-21,2	-4,5	-0,526	-0,434	0,981
-20,1	-4,2	-0,542	-0,563	1,053
-19,0	-4,0	-0,498	-0,421	0,960
-17,7	-3,7	-0,542	-0,575	1,059
-16,4	-3,5	-0,533	-0,415	0,976
-15,0	-3,2	-0,466	-0,593	1,031
-13,4	-2,8	-0,467	-0,392	0,930
-11,6	-2,4	-0,555	-0,620	1,088
-9,5	-2,0	-0,488	-0,343	0,918
-6,7	-1,4	-0,543	-0,714	1,132
0	0	0	0	0
6,7	1,4	0,543	0,714	0,154
9,5	2,0	0,488	0,343	0,111
11,6	2,4	0,555	0,620	0,093
13,4	2,8	0,467	0,392	0,080
15,0	3,2	0,466	0,593	0,070
16,4	3,5	0,533	0,415	0,064
17,7	3,7	0,542	0,575	0,061
19,0	4,0	0,498	0,421	0,056
20,1	4,2	0,542	0,563	0,054
21,2	4,5	0,526	0,434	0,050

Р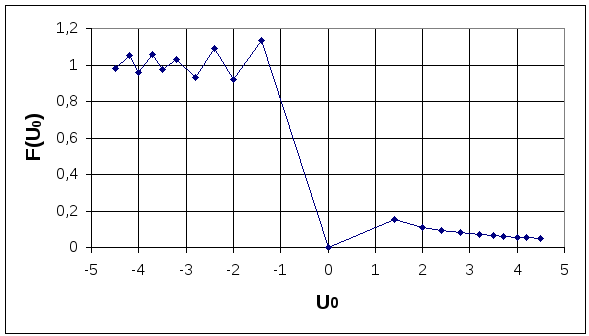исунок 2.4 График зависимости F(U₀) для дифракции на краю экрана от U₀

2.6 Границы зоны Фраунгофера, границы зон Френеля, граница ближней зоны

Для заданного L и λ, с помощью формулы (2.4) определим границы зоны Фраунгофера.

r_m>>2L²/λ 2.4

а с помощью формулы (2.5) определим границы зон Френеля

2.5

Определим границу ближней зоны. Полученные данные занесем в таблицу 2.5.

Таблица 2.5 Границы различных зон

Зоны	Фраунгофера	Френеля	Ближняя зона
rm, м	rm >> 99,75	3,58 ≤ rm ≤ 6683,8	rm ≤ 3,58