АТП-121

Акользин №1

1.Определить значение абсолютной температуры воздуха Т на различных высотах и выдать его на печать. Значение высоты в метрах h (0<h<46000)ввести с клавиатуры. На высоте ниже 11000 метров температура вычисляется как Т=288.16-0.0065h. На высоте от 11000 до 25000 метров температура постоянна и равна 216.16. При высоте выше 25000 метров температура определяется по формуле Т=216.16+0.00276098(h-25000).

2. . Выполнить табулирование функции

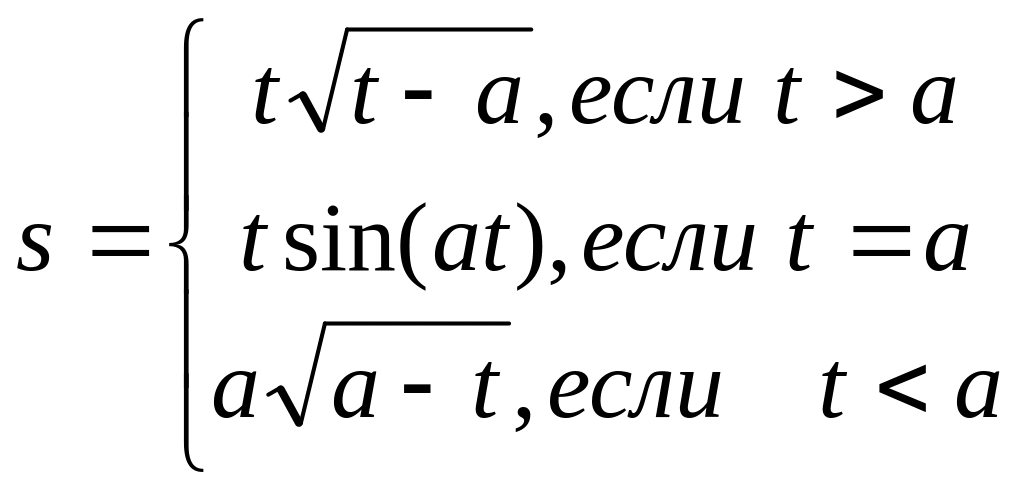
t принадлежит отрезку [1;5], шаг изменения 0,5; а=2,5

3.Ввести массив В(n) целых чисел. Определить количество k отрицательных элементов. Если K>=A(А задается с клавиатуры), то в исходном массиве найти max среди отрицательных элементов и распечатать его. Если K<A, то сделать соответствующее сообщение.

4.Ввести массив A(n). Все положительные элементы массива переписать в массив В. Если его последний элемент больше 2, то заменить его суммой элементов массива. Массив В распечатать.

Кадыгрова №2

1.Значения переменных X, Y, Z поменять местами так, чтобы они оказались упорядоченными по убыванию.

2.Вычислить h=x³-sin(x+1) в интервале 1≤х≤2.5 с шагом х=0.15. для каждого h выполнить следующее:

Если h≥1.5 вычислить A=h³ -16

Если h<1.5 вычислить A=h³ +1/2Sin h.

Выводить на печать А и h.

3.Ввести массив А(n). Переписать его положительные элементы в массив А1, отрицательные – в массив А2, нулевые элементы игнорировать. Вывести на печать больший из массивов.

4. Ввести массив А(n). Найти максимальный по значению элемент массива и увеличить его в два раза. Все остальные элементы массива уменьшить в 10 раз.

Массив отпечатать.

Калашникова №3

1. Вычислить и напечатать:

Значение x ввести с клавиатуры.

2. Дана функция f(x)= 5/(x+1). Найти количество k значений функции, удовлетворяющих неравенству 1<= f(x)<2. Если k>=2, то отпечатать его, если нет – отпечатать соответствующее сообщение. х[n;m]. Шаг по х=0.2. Учесть, что на 0 делить нельзя.

3. Ввести массив А(n) вещественных чисел. Вычислить квадрат разности между минимальным и максимальным элементами массива и записать его на место предпоследнего элемента. Массив распечатать.

4. Ввести массив А(n). Поменять местами минимумы 1-ой и 2-ой половин массива. Массив отпечатать.

Старостин №4

1. Дан номер месяца — целое число в диапазоне 1–12 (1 — январь, 2 — февраль и т. д.). Вывести название соответствующего времени года («зима», «весна», «лето», «осень»). Решение представить в виде вложенных развилок.

2. Ввести В. Если В<10, выдать на печать 2*В. Если В>=10, вычислить и напечатать значения функции y=x²-x+tg(1/B+x) для значений x, изменяющихся от –3 до 1, с шагом 0,1.

3. Ввести массив целых чисел Х(n). Найти среднее арифметическое значений элементов массива, не принадлежащих интервалу [-2;2]. Если среднее арифметическое значение>2, заменить значения первого и последнего элементов на 1, в ином случае – на 0. Массив распечатать.

4. Ввести массив А(n). Найти сумму положительных элементов массива, исключая при этом те элементы, которые кратны трём. Полученной суммой заменить элементы 2-ой половины массива. Массив отпечатать.

Чемогонов №5

1.Даны три переменные: X, Y, Z. Если их значения упорядочены по возрастанию или убыванию, то удвоить их; в противном случае заменить значение каждой переменной на противоположное. 

2. Дана функция f(x)=1/ x⁴. хÎ[n;m]. Шаг по х=0.2. Найти сумму значений функции 0<= f(x)<1. Учесть, что на 0 делить нельзя.

3.Ввести массив К1(n) вещественных чисел. Найти сумму элементов массива. Разделить каждый элемент массива на модуль суммы. Массив распечатать.

4. Ввести массив А(n). Четные элементы массива переписать в массив В, нечетные в С. Вывести на печать тот массив, у которого первый элемент больше.

Поцелуйко №6

1.Значения переменных X, Y, Z поменять местами так, чтобы они оказались упорядоченными по возрастанию. 

2.Вычислить S= где

=

=

Печатать a, b на каждом шаге, сумму S в конце.

3. Ввести массив А(n). Найти его min и max. Все элементы между минимумом и максимумом возвести в квадрат. Массив отпечатать.

4. Ввести массив А(n). Если сумма его первой трети больше суммы элементов последней трети, то заменить элементы второй трети разностью этих сумм, иначе – нулем. Массив распечатать.

Мигович №7

1.Даны три числа. Вывести вначале наименьшее, а затем наибольшее из данных чисел.

2.На интервале -2.1<=x<=0 с шагом по x=0.01 определить максимальное значение функции

Y=|x|-sin x +0.11.

Результат отпечатать.

3.Ввести массив целых чисел В(n). Найти сумму S положительных элементов. Если S>5, поменять местами значения минимального и максимального элементов. Массив распечатать.

4. Ввести массив А(n). Если в массиве больше положительных элементов, то посчитать сумму первой половины массива, иначе – второй половины. Массив и сумму вывести на печать.

Сидоренко №8

1.Даны целые числа x,y. Если хотя бы одно из них четно, найти min из них. В ином случае – выдать сообщение и нечетности.

2.Дана функция f(x)=1/ x³. хÎ[n;m]. Шаг по х=0.5. Найти сумму S1 положительных значений функции и сумму S2 отрицательных значений функции. Если |S1|<|S2|, отпечатать S1, в ином случае - S2. Учесть, что на 0 делить нельзя.

3.Ввести массив В(n) целых чисел. Подсчитать количество k элементов, значение которых принадлежит интервалу [0;5]. Заменить количеством k элементы массива, значение которых меньше нуля. Массив распечатать

4. Ввести массив А(n). Переписать отрицательные элементы его в новый массив В. Найти сумму элементов, заменить ею последний элемент массива А. Оба массива вывести на печать.

Левченко №9

1.Ввести два числа a и b. Если а>b, то найти с= 1/(a²+b² ). Если а=b, выдать об этом сообщение. В противном случае – выяснить, какое из чисел кратно двум и выдать сообщение об этом.

2.Найти среднее арифметическое среди значений функции f(x)= (x+1)², больших 5. На печать выдавать f(x)>5 и среднее арифметическое в конце. хÎ[n;m]. Шаг по х=0.1.

3. Ввести массив А(n) целых чисел. Найти min среди отрицательных элементов, имеющих четное значение. Поставить min на место 2-го, 4-го, 6-го и т.д. элементов. Массив распечатать.

4. Ввести массив А(n). Найти минимальный из положительных элементов матрицы и этим значением заменить все элементы второй половины массива. Массив распечатать.

Привалов №10

1) Составить таблицу значений функций

Y=sin x + cos x

Z= sin x/ cos x – 0.5 x,

x [-2.5;3.5] с шагом по х=0.1. Печатать х, отрицательные у, положительные z на каждом шаге.

2) Ввести массив Х(n) целых чисел. Все элементы массива 3 и кратные 3, заменить на 1; элементы 3, но не кратные заменить на 0; элементы <3 заменить на (-1). Массив распечатать.

3) Ввести массив F(n) вещественных чисел и число Х. Если верно, что min<=X<=max, то массив оставить без изменений, если нет – то умножить все элементы массива на разность между максимумом и минимумом. Массив распечатать.

Русских №11

1) Ввести целое число а. Если а>0, то вычислить максимальное среди значений функции f(x)=e^x/(sin x+cos x) на отрезке [-5;5] с шагом 0.2. В ином случае распечатать все положительные значения функции.

2) Ввести массив А(n) вещественных чисел. Если последний элемент массива отрицательный, то найти max на массиве и заменить его значением последний элемент. Массив распечатать. В ином случае сделать сообщение «Массив не изменен».

3) Ввести массив целых чисел Х(n). определить количество элементов, равных первому элементу массива. Если k>0, то найти сумму положительных элементов массива и заменить ею элементы массива, находящиеся по четным адресам. Массив распечатать.

4) Дано x и y. Вычислить z=x²-5xy+tgy, если y=0. Если y=0, выдать сообщение ‘y=0 ’. Если z<10, напечатать b=12y + e^x+5. Если z>=10 , вычислить и напечатать c=x² + y² -17.5 .