2. Конденсатор

Идеальный емкостный элемент не обладает ни активным сопротивлением (проводимостью), ни индуктивностью. Если к нему приложить синусоидальное напряжение    (см. рис. 4), то ток i  через него будет равен  (3)

П олученный результат показывает, что напряжение на конденсаторе отстает по фазе от тока на  /2. Таким образом, если на входы двухлучевого осциллографа подать сигналы u  и  i, то на его экране будет иметь место картинка, соответствующая рис. 5.

Из (3) вытекает:  ; .

Введенный параметр    называют реактивным емкостным сопротивлением конденсатора. Как и резистивное сопротивление,    имеет размерность Ом. Однако в отличие от Rданный параметр является функцией частоты, что иллюстрирует рис. 6. Из рис. 6 вытекает, что при    конденсатор представляет разрыв для тока, а при       .

Переходя от синусоидальных функций напряжения и тока к соответствующим им комплексам:

; ,

- разделим первый из них на второй:

И ли (4)

В последнем соотношении    - комплексное сопротивление конденсатора. Умножение на   соответствует повороту вектора на угол    по часовой стрелке. Следовательно, уравнению (4) соответствует векторная диаграмма, представленная на рис. 7.

 

3. Катушка индуктивности

Идеальный индуктивный элемент не обладает ни активным сопротивлением, ни емкостью. Пусть протекающий через него ток (см. рис. 8) определяется выражением   . Тогда для напряжения на зажимах катушки индуктивности можно записать

(5)

Полученный результат показывает, что напряжение на катушке индуктивности опережает по фазе ток на  /2. Таким образом, если на входы двухлучевого осциллографа подать сигналы u и i, то на его экране (идеальный индуктивный элемент) будет иметь место картинка, соответствующая рис. 9.

И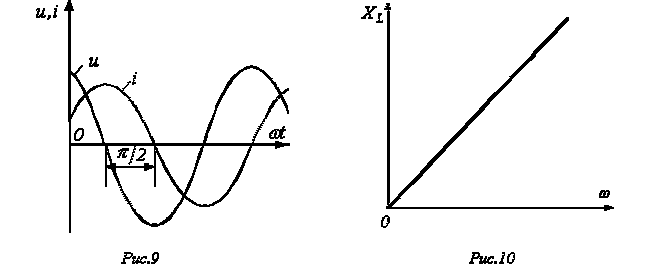 з (5) вытекает:  . Введенный параметр    называют реактивным индуктивным сопротивлением катушки; его размерность – Ом. Как и у емкостного элемента этот параметр является функцией частоты. Однако в данном случае эта зависимость имеет линейный характер, что иллюстрирует рис. 10. Из рис. 10 вытекает, что при    катушка индуктивности не оказывает сопротивления протекающему через него току, и при       .

Переходя от синусоидальных функций напряжения и тока к соответствующим комплексам:

 ;  , разделим первый из них на второй:

или (6)

В полученном соотношении    - комплексное

сопротивление катушки индуктивности. Умножение на    соответствует повороту вектора на угол    против часовой стрелки. Следовательно, уравнению (6) соответствует векторная диаграмма, представленная на рис. 11

132. Основы символического метода расчёта цепей синусоидального тока. Комплексное сопротивление, закон Ома для цепи синусоидального тока.

Символический метод расчета цепей переменного тока.

(разработан американским электротехником Ч. Штейнмецем в 1893-95 гг.)

Так как переменный ток исчерпывающе задается амплитудой вектора и его фазой, то оказалось удобным использовать для его изображения комплексные числа. Комплексным называют число .

Ему соответствует вполне определенная точка на плоскости. При этом комплексное число будем изображать вектором с модулем , углом

Тогда множитель j можно рассматривать как поворотный (он поворачивает вектор против часовой стрелки на 90⁰).

Любое комплексное число может быть записано в различных формах: - алгебраическая форма, - тригонометрическая форма.

П римем . Тогда . Отсюда или .

Решение уравнения .

При , , , т.е. . Тогда , а - показательная форма.

Значительно реже применяется полярная фора записи:

.

При действиях с комплексными числами фактически осуществляется действия с векторами , что и необходимо в цепях переменного тока. При этом сложение и вычитание удобнее производить в алгебраической форме, а умножение и деление - в показательной.

Токи, напряжения, эдс, сопротивления и проводимости в комплексной форме.

Пусть задан ток . Его можно представить в виде: .

и изобразить в виде суммы двух векторов, первый из которых расположен в положительном направлении оси вещественных чисел, а второй - мнимых чисел. Тогда в комплексной форме .

Аналогичным образом можно записать любое напряжение или эдс. При этом вектор, изображающий амплитудные значения, в другом масштабе изображает действующие.

М гновенное значение запишется символически .

По формуле Эйлера .

Поэтому (латинское Imaginarius - мнимый).

Интегралы и производные заданной функции определятся из выражений: , . Откуда следует, что если изображается , то интеграл изображается как , а производная .

Запишем уравнение Кирхгофа для последовательного соединения R, L и C:

На основании изложенного .

Сократив на , получим: , или , или . Отсюда при заданном и параметрах цепи R, L и C легко определяется I .

Величина называется комплексным сопротивлением ветви, содержащей R, L и C. При этом R - положительно, jL - положительно, а - отрицательно.

Величина называется комплексной проводимостью.

Комплексная мощность: Если , а , то , , , (лат. Realis - веществ.), так как - угол сдвига фаз между током и напряжением.

Законы Кирхгофа и Ома в символической форме.

Закон Ома был получен ранее: или . По 1-му закону Кирхгофа для мгновенных значений или в символической (комплексной) форме: . Аналогично для 2-го закона Кирхгофа , или . При записи законов Кирхгофа необходимо приписать всем эдс и токам положительное направление.