Лекция 11
Гидравлический расчет трубопроводов
Основные задачи расчета и классификация трубопроводов
Гидравлический расчет трубопровода производится с целью определения его диаметра, если необходимо обеспечить пропуск определенного количества жидкости, или с целью определения гидравлических потерь при заданных длинах и диаметрах труб, чтобы определить характеристики потока в начальном сечении при обеспечении требуемых параметров потока у потребителей. Решение этих вопросов необходимо и для определения мощности насосной станции, обеспечивающей работу гидравлической системы, что и составляет содержание основной задачи расчета.
Обратная задача – определение расхода и давления на выходе гидросистемы при заданных характеристиках источника гидравлической энергии
Трубопроводы разделяют на простые и сложные. К простым трубопроводам относят такие системы, в которых отсутствуют разветвления. Трубопроводы, в которых есть хотя бы одно разветвление или соединение называют сложными.
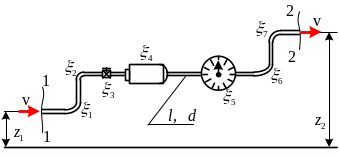
Расчет трубопровода постоянного сечения
Схема трубопровода постоянного сечения
представлена на рис. 11.1. Общая длина
трубопровода
,
а его диаметр
.
Из местных сопротивлений, число которых
может быть произвольным, на схеме
указаны: вентиль, фильтр, поворотное
колено, расходомер. Коэффициент местных
потерь для i-го
сопротивления обозначим
.
Рис. 11.1 |
В начальном сечении трубопровода 1-1
имеем нивелирную высоту
и давление
.
В конечном сечении 2-2 трубопровод имеет
нивелирную высоту
и давление
.
Так как по длине
скорость потока изменяться не будет,
то
.
По соотношению напоров, потерянных на
участках равномерного и неравномерного
движения, простые трубопроводы делятся
на длинные и короткие. В гидравлически
длинном трубопроводе потери напора по
длине существенно превышают местные
потери
;
в гидравлически коротком трубопроводе
местные потери и потери по длине
сопоставимы
,
что и учитывают при составлении уравнения
Бернулли. Более общим является расчет
короткого трубопровода – его и рассмотрим.
Уравнение Бернулли для сечений 1-1 и 2-2 имеет вид
|
|
,
здесь 
;
;
.
Потеря давления на участке между сечениями 1-1 и 2-2 составит
|
|
.Пренебрегая изменением геометрического напора, что допустимо для гидросистем станков и гидравлических манипуляторов, можно записать
|
(11.1) |
.Если определить скорость движения жидкости в трубопроводе через объемный расход
|
|
,то формула для расчета величины падения давления примет вид
|
(11.2) |
,что дает возможность записать зависимость (2) в виде
|
(11.3) |
,где
|
(11.4) |
.
Величину
называют гидравлическим сопротивлением
трубопровода. Размерность параметра
- [
].
Теперь решение задачи о необходимом
давлении на входе в трубопровод (сечение
1-1), при котором на выходе (сечение 2-2)
есть требуемое давление для потребителя
,
дается формулой
|
(11.5) |
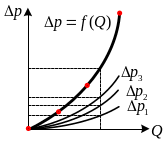
.Зависимость (11.3) называют характеристикой трубопровода. Она показывает изменение суммарных потерь давления в трубопроводе от величины расхода жидкости, подаваемой от источника энергии давления к ее потребителю. Следует обратить внимание на то, что потери давления растут квадрату расхода жидкости (рис.2).
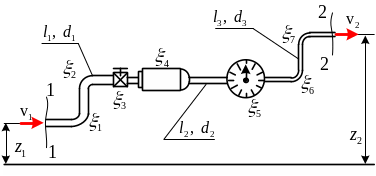
Последовательное соединение трубопроводов разного диаметра
Для каждого
участка трубопровода (рис.11.2) будем
считать известными:
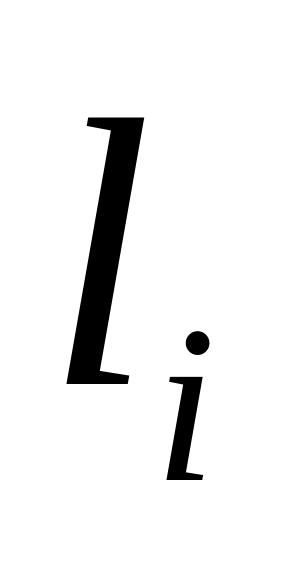− длину трубопровода;
−
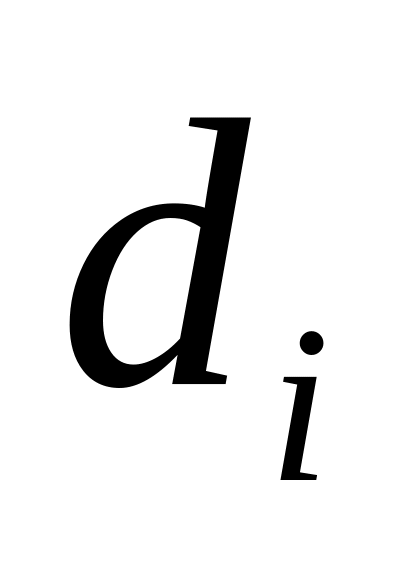диаметр трубопровода;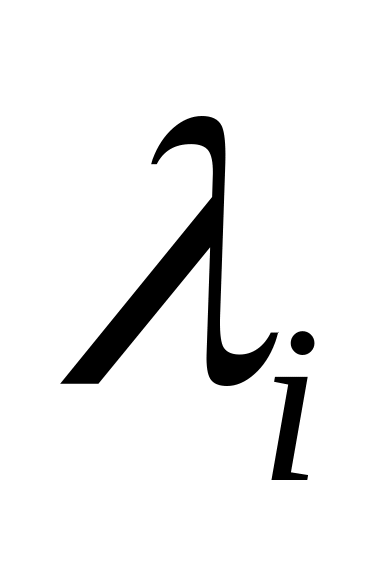
−
коэффициент Дарси;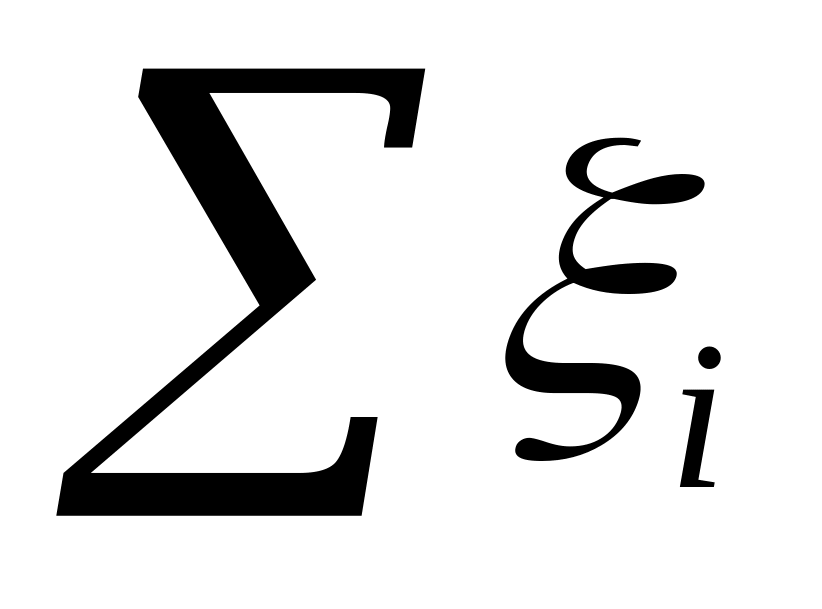
−
сумма коэффициентов местных сопротивлений
на участке.
Рис.11.2 |
Очевидно, что расход на всех участках трубопровода имеет одно значение
|
(11.6) |
;а потеря давления складывается из потерь на отдельных участках
|
(11.7) |
;С учетом обозначения (4) получим
|
(11.8) |
.После введения обозначения
|
|
формула (8) принимает вид
|
(11.9) |
Рис.11.3 |
|
.
Следовательно, можно утверждать, что суммарные потери давления в последовательно соединенных трубопроводах являются суммой потерь в простых трубопроводах. Графически этот результат проиллюстрирован на рис. 11.3.
Для определения энергетической характеристики источника энергии в системе необходимо учесть:
энергию, потребляемую исполнительным органом;
изменение скоростного напора на входе и выходе трубопровода, т.к. диаметры этих участков могут быть разными.
В итоге можно получить величину потребного повышения давления источником энергии на величину
|
(10) |
.Замена скорости потока по формуле
|
|
приводит формулу (10) к виду
|
(11.11) |
,где
|
(11.12) |
.
Здесь
следует рассматривать как общее
гидравлическое сопротивление трубопровода.