Министерство образования РФ

Томский государственный университет

Систем управления и радиоэлектронике

(ТУСУР)

Центр дистанционного обучения.

Кафедра автоматизированных систем управления (АСУ)

Контрольная работа № 2

по дисциплине: «Эконометрика»

Вариант № 2.1

Автор методического пособия: Л.И. Лузина

Задание 1

Найти несмещенную оценку дисперсии несмещенную оценку среднеквадратического отклонения S₁, l = 0,p и оценку ковариационной матрицы вектора , используя данные (в тыс.руб.) о среднедушевых сбережениях (y) и доходах (х) в северных областях России в n=10 семьях. Данные представлены в таб.5.4. Рассматривается линейная модель вида

,

Где М,

Таблица 5,5

№ семьи (i)	1	2	3	4	5	6	7	8	9	10
yi (тыс. руб.)	0,66	0,22	4,84	1,98	8,80	3,74	12,76	5,50	16,50	6,60
xi (млн.руб.)	2,20	4,40	6,60	8,80	11,00	13,20	15,40	17,60	19,80	22,00

Решение:

Найдем несмещенную оценку дисперсии по формуле

.

Оценку ковариационной матрицы вектора определен из выражения

,

а несмещенную оценку среднеквадратического отклонения определим по формуле

,

где - 1-ый диагональный элемент матрицы А = (Х^ТХ)^-1. Тогда, учитывая, что n=10, p=1,получим

,

Таким образом, несмещенная оценка дисперсии равна

а оценка среднеквадратичного отклонения

Найдем оценку ковариационной матрицы вектора :

Задание 2

Дана оценка ковариационной матрицы вектора несмещенных оценок

.

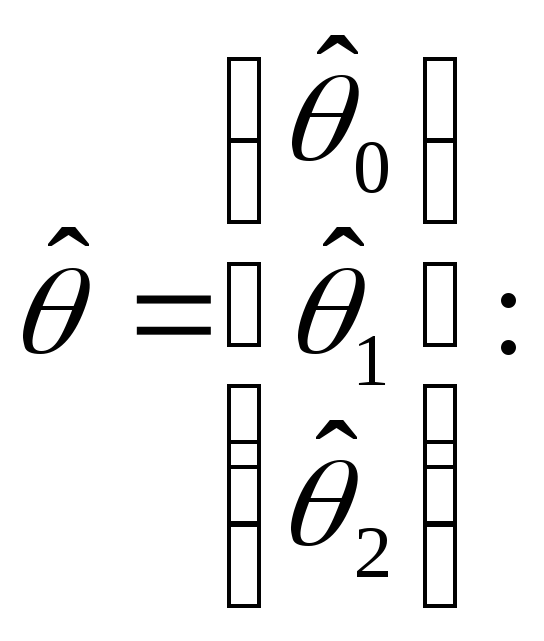
Чему равна оценка дисперсии элемента вектора , то есть:

а) 5,52;

б) 0,04;

в) 0,01;

г) 2,21.

Решение:

в) 0,01;

Задание 3

Пусть а . Показать, что данная оценка является несмещенной.

Решение:

Подставим в формулу вместо Y его выражение

Здесь оценка представлена как сумма истинного (неизвестного нам) значения и линейного комбинации случайных остатков Беря математические ожидания от левого и правого частей с учетом того, что величина и неслучайны, а , получаем:

Тем самым показано, что МНК – оценки (они же ММП – оценки) неизвестных параметров КЛММР являются несмещенными.