
2- 2_Эконометрика
.doc
ТОМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
СИСТЕМ УПРАВЛЕНИЯ И РАДИОЭЛЕКТРОНИКИ (ТУСУР)
Кафедра автоматизированных систем управления (АСУ)
контрольная работа № 2
по дисциплине “Эконометрика”
Вариант 2
2004 г.
Задание
-
Найти несмещенную оценку дисперсии
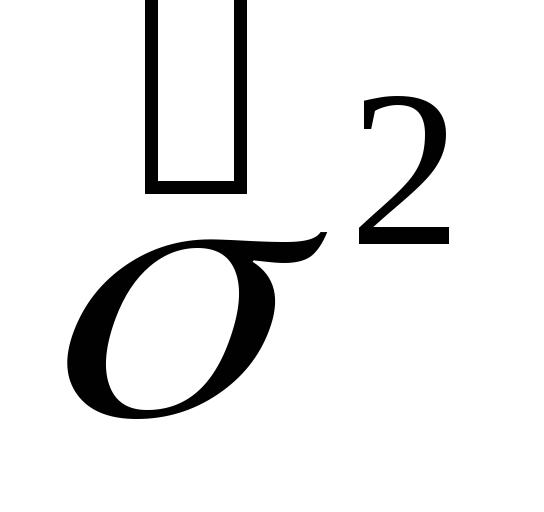 ,
несмещенную оценку среднеквадратического
отклонения
,
несмещенную оценку среднеквадратического
отклонения
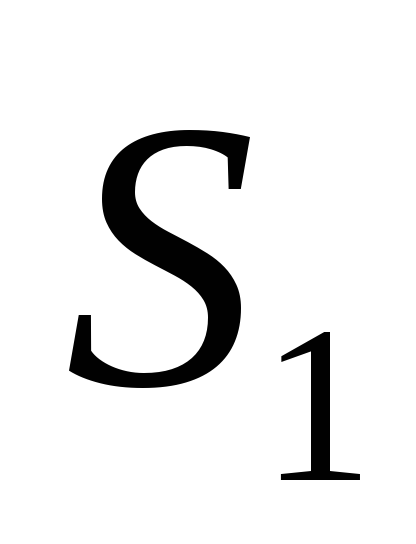 ,
,
 и оценку ковариационной матрицы
и оценку ковариационной матрицы
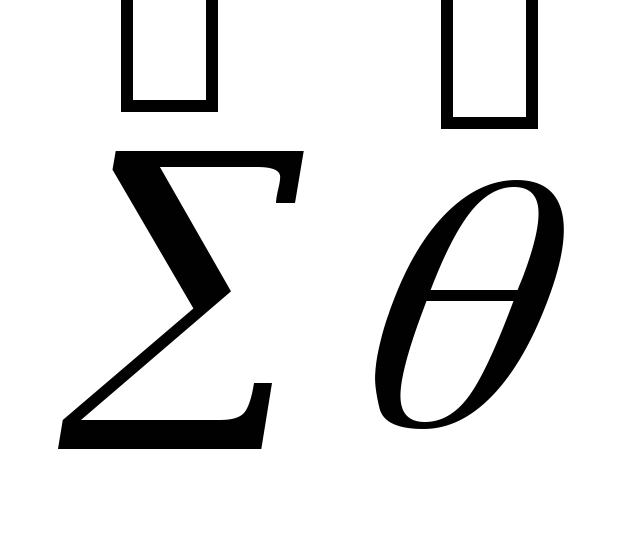 вектора
вектора
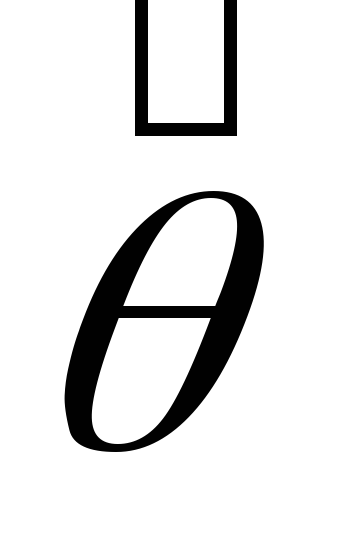 ,
используя данные годовых
отчетов десяти (n=10)
предприятий. Известна
зависимость производительности труда
y (тыс.руб. на чел.) от
объема производства x
(млн. руб), которая представлена в табл.
5.5.
,
используя данные годовых
отчетов десяти (n=10)
предприятий. Известна
зависимость производительности труда
y (тыс.руб. на чел.) от
объема производства x
(млн. руб), которая представлена в табл.
5.5.
Предполагается линейная модель вида
![]() ,
где M
,
где M![]() ,
,
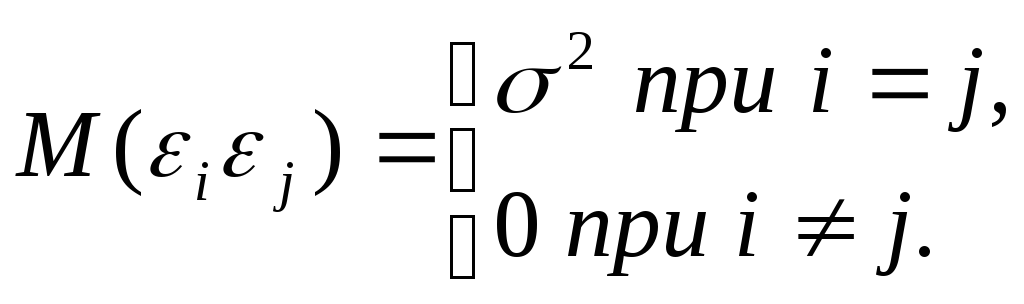
Таблица 5.5.
|
№ пред –приятия ( i ) |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
руб.) |
2,63 |
3,50 |
4,00 |
5,63 |
6,00 |
6,13 |
6,88 |
8,13 |
15,13 |
18,88 |
|
|
3,75 |
5,00 |
6,25 |
6,25 |
6,25 |
6,25 |
7,50 |
8,75 |
18,75 |
25,00 |
Решение
Найдем несмещенную оценку дисперсии по формуле
![]() .
.
С учетом того, что n=10, p =1, получим
![]() .
.
Вектор оценок коэфициентов регрессии можно получить из выражения
![]()
По правилу умножения матриц:

 Найдем
обратную матрицу
Найдем
обратную матрицу
![]()
Следовательно вектор оценок коэффициентов регрессии равен
![]()
Далее

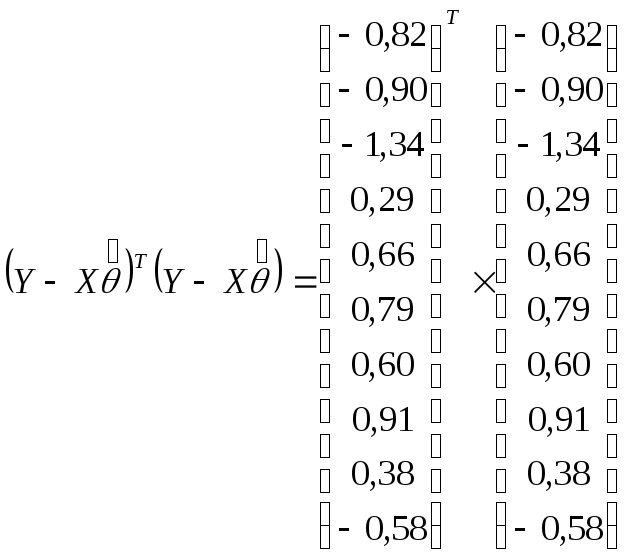 = 0, 6724 + 0, 81 + 1, 7956 + 0, 0841 + 0, 4356 +
0, 6241 + + 0, 36 + 0, 8281 + 0, 1444 + 0, 3364 = 6, 0907
= 0, 6724 + 0, 81 + 1, 7956 + 0, 0841 + 0, 4356 +
0, 6241 + + 0, 36 + 0, 8281 + 0, 1444 + 0, 3364 = 6, 0907
Таким
образом,
![]()
Несмещенную оценку среднеквадратического отклонения определим по формуле
![]() ,
где
,
где
![]() - диагональный элемент матрицы
- диагональный элемент матрицы
![]() .
.
Поскольку
![]() =
0, 306422, а
=
0, 306422, а
![]() получим
получим
![]()
Оценку
ковариационной матрицы вектора
![]() определим из выражения
определим из выражения
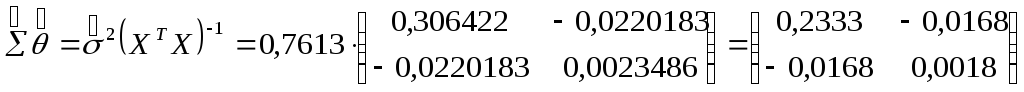
-
Какая оценка
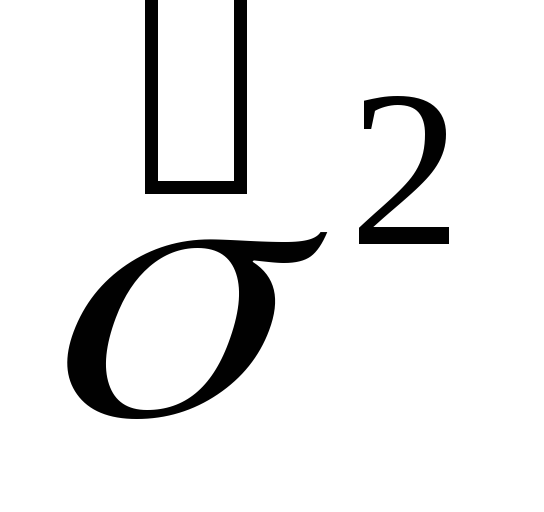 параметра
параметра
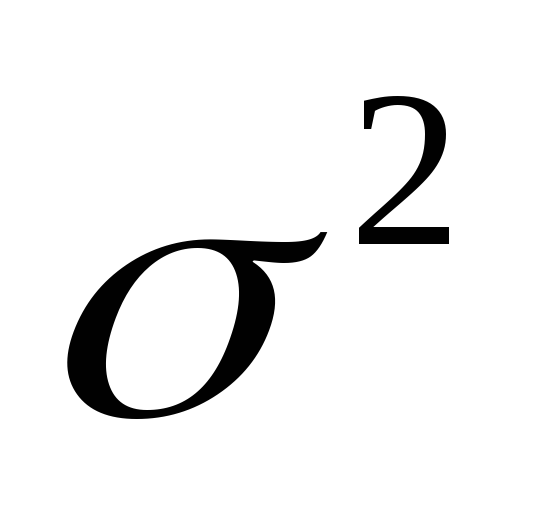 является несмещенной
является несмещенной
а)
![]()
б)
![]()
в)
![]()
г)
![]()
Ответ
в)
![]()
-
Дана оценка ковариационной матрицы вектора несмещенных оценок

Чему
равна оценка дисперсии элемента
![]() вектора
вектора
![]() ,
то есть:
,
то есть:
а) 5,52; б) 0, 04; в) 0, 01; г) 2, 21.
Ответ
Диагональные
элементы ковариационной матрицы
![]() вектора
вектора
![]() задают средние квадраты ошибок
соответствующих оценок. А для несмещенных
оценок это и есть дисперсии оценок.
задают средние квадраты ошибок
соответствующих оценок. А для несмещенных
оценок это и есть дисперсии оценок.
Следовательно правильный ответ
г) 2,21.
