
2- 3_Эконометрика (Контрольная работа_2, вариант_3, учебное пособие «Эконометрика», автор Л.И.Лузина, 2001г
.).doc
Томский межвузовский центр дистанционного образования
Томский государственный университет
систем управления и радиоэлектроники (ТУСУР)
Кафедра автоматизированных систем управления
КОНТРОЛЬНАЯ РАБОТА №2
по дисциплине «Эконометрика»
(Учебное пособие «Эконометрика», автор Л.И. Лузина, 2001 г.)
Выполнил(а):
__________________
студент(ка) ТМЦДО
гр.: ______
специальности 080801
«__» ________ 2008 г.
г. Нижневартовск
2008 г.
Содержание
КОНТРОЛЬНАЯ РАБОТА №2
Вариант №3
Задание 1.
Найти несмещенную
оценку дисперсии
![]() ,
несмещенную оценку среднеквадратического
отклонения
,
несмещенную оценку среднеквадратического
отклонения
![]() ,
,
![]() и оценку ковариационной матрицы
и оценку ковариационной матрицы
![]() вектора
вектора
![]() ,
используя данные (в тыс. руб.) о среднедушевых
сбережениях (y) и доходах (x) в
северных областях России в n=10 семьях.
Данные представлены в табл. 1.1.
Рассматривается линейная модель вида
,
используя данные (в тыс. руб.) о среднедушевых
сбережениях (y) и доходах (x) в
северных областях России в n=10 семьях.
Данные представлены в табл. 1.1.
Рассматривается линейная модель вида
![]() ,
,
где
![]() ,
,
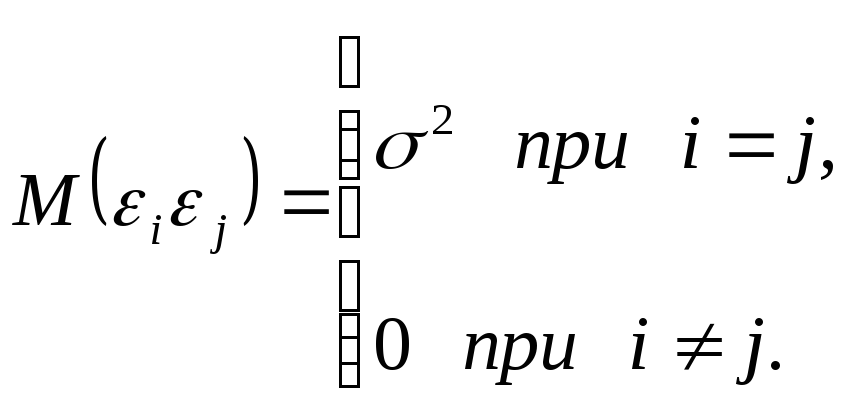
Таблица 1.1
|
№ семьи (i) |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
yi (тыс. руб.) |
0,3 |
0,1 |
2,2 |
0,9 |
4,0 |
1,7 |
5,8 |
2,5 |
7,5 |
3,0 |
|
xi (тыс. руб.) |
1,0 |
2,0 |
3,0 |
4,0 |
5,0 |
6,0 |
7,0 |
8,0 |
9,0 |
10,0 |
Решение.
Определим вектор
оценок
![]() коэффициентов регрессии
коэффициентов регрессии
![]() .
Согласно методу максимального
правдоподобия вектор
.
Согласно методу максимального
правдоподобия вектор
![]() получается из выражения:
получается из выражения:
![]() .
.
Используя правила умножения матриц, получим

 .
.
Найдем обратную матрицу:
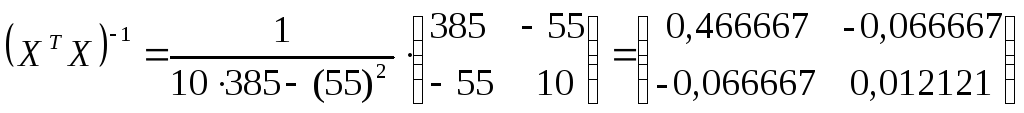 .
.
Тогда вектор оценок коэффициентов регрессии по методу максимального правдоподобия равен
 .
.
Несмещенную оценку дисперсии найдем по формуле
![]() .
.
Оценку ковариационной
матрицы вектора
![]() определим из выражения
определим из выражения
![]() ,
,
Несмещенную оценку среднеквадратического отклонения определим по формуле
![]() ,
,
где
![]() -
l-ый диагональный элемент матрицы
-
l-ый диагональный элемент матрицы
![]() .
Тогда, учитывая, что n=10, p=1,
получим
.
Тогда, учитывая, что n=10, p=1,
получим
![]() .
.


Таким образом,
несмещенная оценка дисперсии равна
![]() ,
,
а оценка
среднеквадратичного отклонения
![]() .
.
Определим несмещенную оценку среднеквадратического отклонения
![]() .
.
Найдем оценку
ковариационной матрицы вектора
![]()
 .
.
Ответ:
![]() ,
,
![]() ,
,
![]() .
.
Задание 2.
По данным n=15
фирм исследована зависимость прибыли
y от числа работающих x вида
![]() .
Была получена оценка дисперсии
.
Была получена оценка дисперсии
![]() и обратная матрица
и обратная матрица
 .
Определить оценку ковариационной
матрицы
.
Определить оценку ковариационной
матрицы
![]() .
.
Решение.
Оценка ковариационной
матрицы
![]() определяется
по формуле
определяется
по формуле
![]() .
.
Подставляя значения в формулу, получаем
 .
.
Ответ:
![]() .
.
Задание 3.
Какая оценка
![]() параметра
параметра
![]() является несмещенной
является несмещенной
-
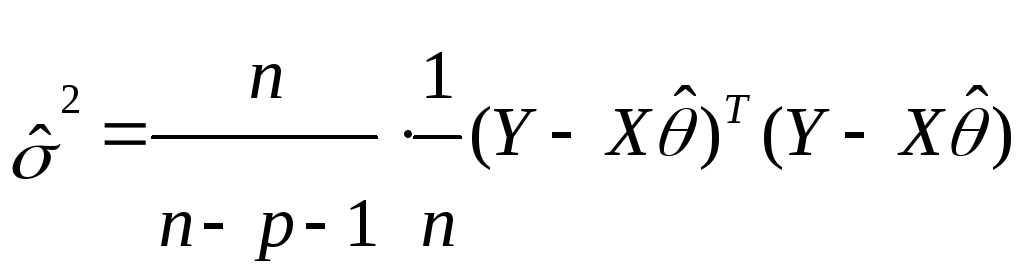 ;
; -
 ;
; -
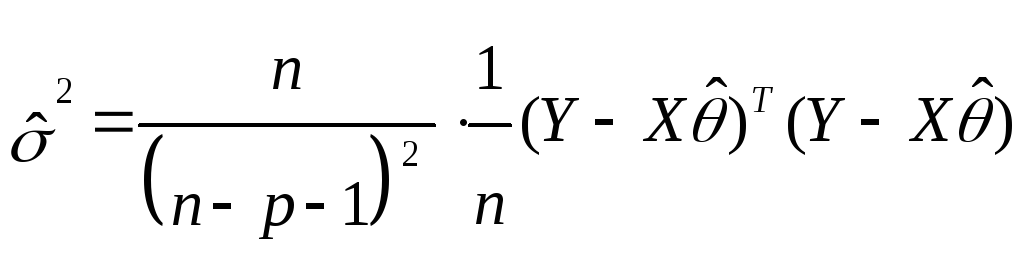 .
.
Решение.
Оценка
 параметра
параметра
![]() является несмещенной.
является несмещенной.
Ответ: а).
Используемая литература
-
Айвазян С.А., Мхитарян В.С. Прикладная статистика и основы эконометрики. – М. Юнити, 1998. – 1022 с.
-
Лузина Л.И. Эконометрика: Учебное пособие. – Томск: Томский межвузовский центр дистанционного образования, 2001. – 75 с.
