
- •Пояснительная записка
- •Геометрическая интерпретация комплексного числа.
- •Математический анализ Дифференциальное и интегральное исчисление
- •Теоретический материал
- •Определители квадратной матрицы и их свойства.
- •Правило Саррюса или правило треугольника:
- •Решение систем линейных уравнений методом Крамера.
Математический анализ Дифференциальное и интегральное исчисление
По данной теме изучите теорию. Затем ознакомьтесь с методическими указаниями по этой теме и внимательно разберите решение примеров из данного пособия.
Функция F(x) называется первообразной для функции f(x), если (F(x))’=f(x).
Первообразная определена неоднозначно: если F(x) – первообразная для функции f(x), то F(x)+C – также первообразная для данной функции.
Множество
всех первообразных для функции f(x)
называется неопределенным интегралом
и обозначается
 ,
где f(x)
– подынтегральная функция, f(x)dx
– подынтегральное выражение, С –
произвольная постоянная (С = const),
,
где f(x)
– подынтегральная функция, f(x)dx
– подынтегральное выражение, С –
произвольная постоянная (С = const),
 - знак операции интегрирования, d
– знак операции дифференцирования.
- знак операции интегрирования, d
– знак операции дифференцирования.
Свойства неопределенного интеграла:
1.

 ,
где с = const.
,
где с = const.
2.

 .
.
3.
 .
.
Таблица 1 (неопределенных интегралов)
1. 2.
3.
4. 5.
6.
7.
8.
|
9.
10.
11.
12.
13.
14.
15.
|
Примеры. Найти неопределенный интеграл:
а)
 ;
б)
;
б)
 ;
в)
;
в)![]() ;
г)
;
г)
![]() .
.
Решение: а) ,чтобы найти данный неопределенный интеграл, воспользуемся методом разложения, который заключается в разложении подынтегральной функции на сумму функций и использовании свойств неопределенного интеграла 1 и 2.
= =
= =(св-во
2) =
=(св-во
2) =
= = (св-во 1) =
= (св-во 1) =
 =(используем
формулы 3 и 4 из таблицы 1)=
=(используем
формулы 3 и 4 из таблицы 1)=
 =
= .
.
Ответ: = .
б)
![]() .
Данный интеграл вычисляется методом
замены переменной (линейная замена).
Обозначим выражение в скобках через t:
3х – 1 = t,
тогда d(3х – 1)=dt
=> 3dх = dt
=>
.
Данный интеграл вычисляется методом
замены переменной (линейная замена).
Обозначим выражение в скобках через t:
3х – 1 = t,
тогда d(3х – 1)=dt
=> 3dх = dt
=>![]() .
.
=
 =
=
 =
(по формуле 3 из таблицы 1 н.и.) = =
=
(по формуле 3 из таблицы 1 н.и.) = = =
=
 =
=
 .
Ответ:
=
.
.
Ответ:
=
.
в)
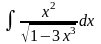 .
Здесь при вычислении интеграла
используется также метод замены
.
Здесь при вычислении интеграла
используется также метод замены
переменной
(нелинейная замена).
=
 =
=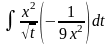 =
= =
=
 = (используем формулу 4 из табл.1) =
= (используем формулу 4 из табл.1) =
 =
=
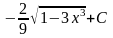 .
.
Ответ: = .
Для
вычисления определенных интегралов
используется формула Ньютона-Лейбница: ,
(где а – нижний предел интегрирования,
b – верхний предел,
F(x)
– первообразная для функции f(x).
Для нахождения первообразной F(x)
используются те же методы, что и при
вычислении неопределенных интегралов).
,
(где а – нижний предел интегрирования,
b – верхний предел,
F(x)
– первообразная для функции f(x).
Для нахождения первообразной F(x)
используются те же методы, что и при
вычислении неопределенных интегралов).
Решение.
а)
 =
(формула 9 табл. 1) =
=
(формула 9 табл. 1) =
 =
=
 .
.
Ответ:
=
 .
б) Используем метод замены переменной:
.
б) Используем метод замены переменной:
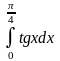 =
=
 =
=
 =
=
 =
(по формуле 3 табл.1 н.и.)=
=
(по формуле 3 табл.1 н.и.)=
 =
=
 =
(т.к. ln1 = 0)=
=
(т.к. ln1 = 0)= =
=
 .
Ответ:
=
.
Ответ:
=
 .
.
В
отличие от метода замены для неопределенных
интегралов, для определенных интегралов
нет необходимости возвращаться к старой
переменной интегрирования (х), если
перейти к новым пределам интегрирования
(в нашем примере старыми пределами былиа
= 0, b =
 ,
а новыми стали а = 1, b
=
,
а новыми стали а = 1, b
=
 ).
).
Дифференциальные уравнения первого порядка с разделяющимися переменными.
Обыкновенные дифференциальные уравнения. Дифференциальным уравнением называется уравнение, связывающее между собой независимую переменную x, искомую функцию y и её производные или дифференциалы.
Символически дифференциальное уравнение записывается так:
F(x,y,y')=0, F(x,y,y")=0, F(x,y,y',y",.., y(n))=0
Дифференциальное уравнение называется обыкновенным, если искомая функция зависит от одного независимого переменного.
Решением
дифференциального уравнения называется
такая функция ![]() ,
которая обращает это уравнение в
тождество. Порядком
дифференциального уравнения называется
порядок старшей производной, входящей
в это уравнение
,
которая обращает это уравнение в
тождество. Порядком
дифференциального уравнения называется
порядок старшей производной, входящей
в это уравнение
Примеры.
1.
Рассмотрим дифференциальное уравнение
первого порядка
![]() Решением этого уравнения является
функция y = 5 ln x. Действительно,
Решением этого уравнения является
функция y = 5 ln x. Действительно, ![]() ,
подставляя y' в
уравнение, получим
,
подставляя y' в
уравнение, получим ![]() –
тождество.
–
тождество.
Это значит, что функция y = 5 ln x– есть решение этого дифференциального уравнения.
2.
Рассмотрим дифференциальное уравнение
второго порядка y"
- 5y' +6y = 0. Функция ![]() –
решение этого уравнения.
–
решение этого уравнения.
Действительно, ![]() .
Подставляя эти выражения в уравнение,
получим:
.
Подставляя эти выражения в уравнение,
получим: ![]() ,
,![]() –
тождество. А это и значит, что функция
–
тождество. А это и значит, что функция ![]() –
есть решение этого дифференциального
уравнения.
–
есть решение этого дифференциального
уравнения.
Общим
решением дифференциального
уравнения называется
функция вида ![]() ,в
которую входит столько независимых
произвольных постоянных, каков порядок
уравнения. Частным
решением дифференциального
уравнения называется
решение, полученное из общего решения
при различных числовых значениях
произвольных постоянных. Значения
произвольных постоянных находится при
определённых начальных значениях
аргумента и функции.
,в
которую входит столько независимых
произвольных постоянных, каков порядок
уравнения. Частным
решением дифференциального
уравнения называется
решение, полученное из общего решения
при различных числовых значениях
произвольных постоянных. Значения
произвольных постоянных находится при
определённых начальных значениях
аргумента и функции.
График частного решения дифференциального уравнения называется интегральной кривой.
Примеры
1.Найти частное решение дифференциального уравнения первого порядка
xdx + ydy = 0, если y = 4 при x = 3.
Решение.
Интегрируя обе части уравнения, получим ![]()
Замечание.
Произвольную постоянную С, полученную
в результате интегрирования, можно
представлять в любой форме, удобной для
дальнейших преобразований. В данном
случае, с учётом канонического уравнения
окружности произвольную постоянную С
удобно представить в виде ![]() .
.
![]() -
общее решение дифференциального
уравнения.
-
общее решение дифференциального
уравнения.
Частное решение уравнения, удовлетворяющее начальным условиям y = 4 при x = 3 находится из общего подстановкой начальных условий в общее решение: 32 + 42= C2; C=5.
Подставляя С=5 в общее решение, получим x2 +y2 = 52.
Это есть частное решение дифференциального уравнения, полученное из общего решения при заданных начальных условиях.
2.
Найти общее решение дифференциального
уравнения ![]() Решением этого уравнения является
всякая функция вида
Решением этого уравнения является
всякая функция вида ![]() ,
где С – произвольная постоянная.
Действительно, подставляя в уравнения
,
получим:
,
где С – произвольная постоянная.
Действительно, подставляя в уравнения
,
получим:  ,
, ![]() .
.
Следовательно,
данное дифференциальное уравнение
имеет бесконечное множество решений,
так как при различных значениях постоянной
С равенство
определяет
различные решения уравнения ![]() .
Например, непосредственной подстановкой
можно убедиться, что функции
.
Например, непосредственной подстановкой
можно убедиться, что функции ![]() являются
решениями уравнения
.
являются
решениями уравнения
.
Задача, в которой требуется найти частное решение уравнения y' = f(x,y) удовлетворяющее начальному условию y(x0) = y0, называется задачей Коши.
Решение уравнения y' = f(x,y), удовлетворяющее начальному условию, y(x0) = y0, называется решением задачи Коши.
Решение задачи Коши имеет простой геометрический смысл. Действительно, согласно данным определениям, решить задачу Коши y' = f(x,y) при условии y(x0) = y0,, означает найти интегральную кривую уравнения y' = f(x,y) которая проходит через заданную точку M0(x0,y0).
Дифференциальные уравнения первого порядка Дифференциальным уравнением первого порядка называется уравнение вида F(x,y,y') = 0. В дифференциальное уравнение первого порядка входит первая производная и не входят производные более высокого порядка.
Уравнение y' = f(x,y) называется уравнением первого порядка, разрешённым относительно производной.
Общим
решением дифференциального уравнения
первого порядка называется функция
вида ![]() ,
которая содержит одну произвольную
постоянную.
,
которая содержит одну произвольную
постоянную.
Пример. Рассмотрим
дифференциальное уравнение первого
порядка ![]() .
.
Решением
этого уравнения является функция ![]() .
.
Действительно,
заменив в данном уравнении, ![]() его
значением, получим
его
значением, получим

![]() то
есть 3x=3x
то
есть 3x=3x
Следовательно, функция является общим решением уравнения при любом постоянном С.
Найти
частное решение данного уравнения,
удовлетворяющее начальному
условию y(1)=1 Подставляя
начальные условия x
= 1, y =1 в общее
решение уравнения
,
получим ![]() откуда C
= 0.
откуда C
= 0.
Таким
образом, частное решение получим из
общего
подставив
в это уравнение, полученное значение C
= 0 ![]()
![]() –
частное решение.
–
частное решение.
Дифференциальные
уравнения с разделяющимися переменными
Дифференциальным
уравнением с разделяющимися переменными
называется уравнение вида:y'=f(x)g(y) или
через дифференциалы ![]() ,
где f(x)
и g(y)–
заданные функции.
,
где f(x)
и g(y)–
заданные функции.
Для
тех y,
для которых ![]() ,
уравнение y'=f(x)g(y) равносильно
уравнению,
,
уравнение y'=f(x)g(y) равносильно
уравнению, ![]() в
котором переменная y присутствует
лишь в левой части, а переменная x- лишь
в правой части. Говорят, «в
уравнении y'=f(x)g(y разделим
переменные».
в
котором переменная y присутствует
лишь в левой части, а переменная x- лишь
в правой части. Говорят, «в
уравнении y'=f(x)g(y разделим
переменные».
Уравнение вида называется уравнением с разделёнными переменными.
Проинтегрировав обе части уравнения по x, получим
G(y)
= F(x) + C– общее решение
уравнения, где G(y) и F(x) –
некоторые первообразные соответственно
функций ![]() и f(x), C
- произвольная
постоянная.
и f(x), C
- произвольная
постоянная.
Алгоритм решения дифференциального уравнения первого порядка с разделяющимися переменными
Производную функции переписать через её дифференциалы

Разделить переменные.
Проинтегрировать обе части равенства, найти общее решение.
Если заданы начальные условия, найти частное решение.
Пример. Решить уравнение y' = xy
Решение. Производную
функции y' заменим
на ![]()
![]()
разделим
переменные ![]()
![]()
проинтегрируем обе части равенства:
 Ответ:
Ответ: ![]()
Основы теории вероятности и математической статистики
По данной теме изучите теорию. Затем ознакомьтесь с методическими указаниями по этой теме и внимательно разберите решение примеров из данного пособия.
К числу основных понятий теории вероятностей относятся: событие, вероятность события и относительная частота появления события при испытаниях. Математическая статистика-это раздел математики, который изучает методы сбора, систематизации, обработки и использования статистических данных для принятия решения. Сущность математической статистики заключается в установлении закономерностей, которым подчинены массовые случайные явления.
Суммой конечного числа событий называется событие, состоящее в наступлении хотя бы одного из них. Сумму двух событий обозначают символом А+В, а сумму n событий символом А1+А2+ : +Аn.
Теорема
сложения вероятностей.
Вероятность суммы двух несовместных
событий равна ![]() сумме
вероятностей
этих событий.
сумме
вероятностей
этих событий.
![]() или
или
![]()
Следствие 1. Если событие А1, А2, : ,Аn образуют полную систему, то сумма вероятностей этих событий равна единице.
![]() .
.
Следствие
2. Сумма
вероятностей противоположных
событий ![]() и
и ![]() равна
единице.
равна
единице.
![]() .
.
Признак Даламбера.
Если
для ряда с положительными членами
![]() выполняется
условие
выполняется
условие
![]() , то ряд сходится при l<1 и расходится
при l>1.. Признак Даламбера не дает
ответа, если l=1 этом случае для исследования
ряда применяются другие методы.
, то ряд сходится при l<1 и расходится
при l>1.. Признак Даламбера не дает
ответа, если l=1 этом случае для исследования
ряда применяются другие методы.
Пример.
Исследовать на сходимость ряд:
1)![]() ;
2)
;
2)![]() ;
3)
;
3)
![]() ;
;
Решение:
1)![]()
Ряд сходится.
2)![]()
Ряд сходится.
 Ряд
расходится.
Ряд
расходится.



 n
≠ –1;
n
≠ –1;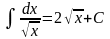 ;
; ;
; ;
; ;
; ;
; ;
;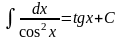
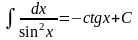 ;
; (|x|<a,
a≠0);
(|x|<a,
a≠0); (a≠0);
(a≠0); (|x|≠a,
a≠0);
(|x|≠a,
a≠0); .
.