МИНИСТЕРСВО ТРАНСПОРТА РОССИЙСКОЙ ФЕДЕРАЦИИ

ФЕДЕРАЛЬНОЕ АГЕНТСТВО ЖЕЛЕЗНОДОРОЖНОГО ТРАНСПОРТА

Саратовский техникум железнодорожного транспорта - филиал федерального государственного бюджетного образовательного учреждения высшего профессионального образования

«Самарский государственный университет путей сообщения»

СТЖТ – филиал СамГУПС

Методические указания

по выполнению Контрольной работы по учебной дисциплине

ЕН.01 Прикладная математика

для студентов заочного обученияспециальностей:

27.02.03Автоматика и телемеханика на транспорте (на железнодорожном транспорте),

23.02.01 Организация перевозок и управление на транспорте (по видам), 08.02.10 Строительство железных дорог, путь и путевое хозяйство,

23.02.06 Техническая эксплуатация подвижного состава железных дорог,

13.02.07 Электроснабжение (по отраслям)

Саратов 2015

ОДОБРЕНО

на заседании ЦМК «Математика,

информатика и ИКТ»

Протокол № ___ от «__» _____ 20__ г.

Председатель

__________________ /Полкова С.И../

УТВЕРЖДАЮ

Зам. директора по УР ____________________________/Моисеева Т.В./

«___» ___________20__ г.

Составители:

Воротилова Е.А.- преподаватель первой квалификационной

категории СТЖТ - филиала СамГУПС.

Рецензенты:

Внутренний

Полкова С.И. - преподаватель высшей квалификационной категории

СТЖТ - филиала СамГУПС

Пояснительная записка

Одной из основных задач предмета «Математика» для средних специальных заведений состоит в том, чтобы вооружить студентов основами математических знаний и умений в объёме необходимом для практической деятельности , для усвоения общетехнических и специальных предметов, а также для дальнейшего повышения квалификации путём самообразования.

Контрольная работа по учебной дисциплине ЕН.01 Прикладная математика проводится в соответствии с требованием рабочей программы для студентов, обучающихся на заочном отделении по специальностям: 27.02.03Автоматика и телемеханика на транспорте (на железнодорожном транспорте), 23.02.01Организация перевозок и управление на транспорте (по видам), 08.02.10 Строительство железных дорог, путь и путевое хозяйство, 23.02.06 Техническая эксплуатация подвижного состава железных дорог, 13.02.07 Электроснабжение (по отраслям),с целью определения качества знаний студентов.

В результате освоения учебной дисциплины обучающийся должен

уметь:

• решать прикладные электротехнические задачи методом комплексных чисел;

• определять основные свойства числовых функций, иллюстрировать их на графиках;

• строить графики функций изученных функций, иллюстрировать по графику свойства функций;

использовать понятие функции для описания и анализа зависимостей величин.

- применять математические методы дифференциального и интегрального исчисления длярешения профессиональных задач;

- применять основные положения теории вероятностей и математической статистики впрофессиональной деятельности;

- использовать приемы и методы математического синтеза и анализа в различных профессиональных ситуациях;

В результате освоения учебной дисциплины обучающийся должен

знать:

• основные понятия о математическом синтезе и анализе

.

- способы решения прикладных задач методом комплексных чисел

Требования к выполнению и оформлению контрольной работы

Контрольную работу следует выполнять самостоятельно. При решении задач следует обосновывать каждый шаг решения, исходя из теоретических основ курса. Не следует применять формулы, которые не входят в программу. Решение должно быть доведено до окончательного ответа.

1. Работа выполняется в отдельной тетради школьного формата. Следует пронумеровать страницы и оставить на них поля не менее 3 смдля замечаний преподавателя.

2. На обложке тетради должны быть аккуратно записаны все данные титульного листа: шифр, специальность, если она не отражена шифре, фамилия, имя, отчество студента, предмет.

3. Каждую задачу нужно начинать с новой страницы.

4. Решение задач желательно располагать в порядке номеров, указанных в задании.

5. Условие задач должны быть обязательно записаны в тетрадь.

6. При оформлении записей в тетради необходимо выполнять общие требования к культуре их ведения.

7. Работа должна быть выполнена чернилами одного цвета, аккуратно и разборчиво.

8. Решения задач должны сопровождаться краткими, но достаточно обоснованными пояснениями, используемые формулы нужно выписывать.

9. Чертежи следует выполнять карандашом с использованием чертёжных инструментов, соблюдая масштаб.

10. В конце работы следует указать список используемых источников, поставить дату выполнения работы и подпись.

11. Если в работе допущены недочёты и ошибки, то учащийся должен выполнить все указания преподавателя, сделанные в рецензии.

12. Контрольная работа должна быть выполнена в срок (в соответствии с планом-графиком). В период сессии работы на проверку не принимаются.

13. Работа, выполненная не по своему варианту, не учитывается и возвращается студенту без оценки.

14. Учащиеся, не имеющие зачёта по контрольной работе, к экзамену не допускаются.

15. Во время экзамена зачтённые контрольные работы представляются преподавателю вместе с данными методическими указаниями.

16. Контрольная работа имеет 100 вариантов. Вариант работы выбирается по двум последним цифрам шифра согласно представленной таблице.

В процессе изучения учебной дисциплины студент-заочник должен выполнить одну контрольную работу.

После выполнения контрольной работы и практических заданий в сроки, предусмотренные учебным графиком, для проверки знаний студентов проводится экзамен.

Методические указания

к выполнению задач контрольной работы

Линейная алгебра

Комплексные числа.

По данной теме изучите теорию. Затем ознакомьтесь с методическими указаниями по этой теме и внимательно разберите решение примеров из данного пособия.

Основные понятия и определения. Решение многих задач сводится к решению алгебраических уравнений. Поэтому исследование алгебраических уравнений является одним из важнейших вопросов математики. Стремление сделать уравнение разрешимым - одна из главных причин расширения понятия числа.

Рациональные и иррациональные числа образуют множество R действительных чисел. Однако действительных чисел недостаточно для того, чтобы решить уравнение. Корень уравнения или называется мнимой единицей и обозначается буквой i. Таким образом, символ i удовлетворяет условию

Комплексным числом называется число видаa+bi, где aи b – действительные числа, аi - мнимая единица.

Число а называется действительной частью комплексного числа, а число bi – мнимой частью.

Запись комплексного числа в виде z= a+bi называется алгебраической формой записи комплексного числа.

Два комплексных числа и называются равнымитогда и только тогда, когда равны их действительные части и коэффициенты при мнимой части.

Понятия«больше» и «меньше» для комплексных чисел не определяются.

Комплексные числа a+bi и a-biназываются сопряжёнными, а комплексные числаa+bi и -a-bi называются противоположными комплексными числами.

Действия над комплексными числами в алгебраической форме.

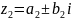Суммой двух комплексных чисел и называется комплексное число .

Произведением комплексных чисел называется комплексное число.

Вычитание комплексных чисел вводится как операция, обратная сложению; деление комплексных чисел как операция, обратная умножению. При делении на комплексное число достаточно умножить числитель и знаменатель дроби на число сопряжённое знаменателю

Пример 1. Найти сумму и разность комплексных чисел и .

Решение. Сумму находим сложением двучленов :

Произведение находим перемножением двучленов с последующей заменой на -1.

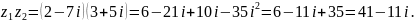
Пример 2. Даны комплексные числа 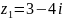и . Найти разность и частное .

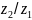Решение. Разность находим вычитанием двучленов и :

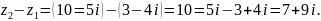
Чтобы найти частное , умножим числитель и знаменатель этой дроби на число, сопряженное знаменателю :