1 Контрольная работа / 1- 7_Химия (1контр-вар7_Химия.doc)

8

Томский межвузовский центр дистанционного образования

Томский государственный университет

систем управления и радиоэлектроники (ТУСУР)

Контрольная работа № 1

по дисциплине «Химия»

авторы учебного пособия:

Смирнов Г.В.

Якунина Г.Н.

вариант №7

1) Закончить уравнения реакций

а) Pb(NO₃)₂ + 2NaOH = Pb(OH)₂ + 2NaN0₃

Pb²⁺ + 2N + 2Na⁺ + 2O = Pb(OH)₂ + 2Na⁺ + 2N

Pb²⁺ + 2O = Pb(OH)₂

б) 2Pb + O₂ = 2PbO

в) PbO + 2NaOH = Na₂PbO₂ + H₂O

PbO + 2Na⁺ + 2O = 2Na⁺ + Pb + H₂O

PbO + 2O= Pb+ H₂O

г) Pb(OH)NO₃ + HNO₃ = Pb(NO₃)₂+ H₂O

PbOH⁺ + N + H⁺+ N = Pb²⁺ + 2N + H₂O

PbOH⁺ + = Pb²⁺+ H₂O

д) PbH₄ Pb + 2H₂

е) PbH₄ +2O₂ PbO₂ + 2H₂O

ж) SnCl₄ + 4NaOH = Sn(OH)₄ + 4NaCl

Sn⁴⁺ + 4+ 4Na⁺ +4O= Sn(OH)₄ + 4Na⁺ + 4

Sn⁴⁺ + 4O= Sn(OH)₄

з) CuSO₄ + Fe = FeSO₄ + Cu

Cu²⁺ + S+ Fe⁰ = Fe²⁺ + S+ Cu⁰

Cu²⁺ + Fe⁰ = Fe²⁺ + Cu⁰

и) Cu(OH)₂ CuO + H₂O

к) Ga + As = GaAs

По реакции (д) получают свинец, пластичность которого допускает изготовление его в рулонах (рольный свинец). Рольный свинец применяют для защиты металлических стенок различных реакторов. Для защиты аппаратов применяют и свинцевание – непосредственное нанесение на поверхность металла гомогенного слоя свинца. Для защиты от атмосферной коррозии толщина покрытия должна составлять 0,1– 0,2 мм. Для защиты химической аппаратуры толщина защитного слоя достигает 16 мм.

С помощью реакции (з) железную конструкцию покрывают слоем меди. Это пример катодной защиты железной конструкции от коррозии.

а) 2Mn(OH)₃ + H₂CO₃ = (Mn(OH)₂)₂CO₃ + 2H₂O

двухосновный

карбонат марганца (III)

H – O

Mn – O

H – O

C = O

H – O

Mn – O

H – O

б) Mn(OH)₃ + H₂CO₃ = MnOHCO₃ + 2H₂O

одноосновный

карбонат марганца (III)

O

H – O – Mn C = O

O

в) 2Mn(OH)₃ + 3H₂CO₃ = Mn₂(CO₃)₃ + 6H₂O

карбонат

марганца(III)

O –– C = O

Mn –– O

O

C = O

O

Mn –– O –– C = O

O

г) Mn(OH)₃ + 3H₂CO₃ = Mn(HCO₃)₃ + 3H₂O

гидрокарбонат

марганца (III)

O – H

|

O –– C = O

Mn –– O –– C = O

|

O – H

O –– C = O

|

O – H

2. Дано: ∆(NH₃) = - 46,19 кДж/моль

t₁ = 25˚C ∆(O₂) = 0 кДж/моль

t₂ = 500˚C ∆(H₂O_ж) = - 241,84 кДж/моль

__________ ∆(NO) = 90,34 кДж/моль

∆G₂₉₈ – ? (NH₃) = 192,5 Дж/(моль*к)

∆G₇₇₃ – ? (O₂) = 205,03 Дж/(моль*к)

(H₂O_ж) = 188,74 Дж/(моль*к)

(NO) = 210,62 Дж/(моль*к)

Решение:

4NH₃ + 5O₂ = 6H₂O_(ж) + 4NO

∆= ∑ ∆ – ∑ ∆= 6∆+ 4∆– 4∆– 5∆= 6*(-241,84) +

+ 4*90,37 – 4*(-46,19) – 5*0 = -904,8 кДж

∆ = ∑ – ∑ = 6+ 4– 4– 5= 6*188,74 + 4*210,62 –

– 4*192,5 – 5*205,03 = 179,77 Дж = 0,17977 кДж

T₁ = 25 + 273 = 298 K

∆G₂₉₈ = ∆– T∆S = -904,8 кДж – 298*0,17977 = -958,4 кДж

Такое значение ∆G₂₉₈ указывает на то, что реакция протекает в прямом направлении.

T₂ = 500 + 273 = 773 K

∆G₇₇₃ = -904,8 – 773*0,17977 = -1043,8кДж

∆G₇₇₃ имеет более отрицательное значение, чем ∆G₂₉₈, следовательно, реакция продолжает протекать в прямом направлении. Таким образом, повышение температуры на направление данной реакции не влияет.

Количество теплоты, выделившейся или поглотившейся в результате реакции, зависит только от относительного запаса энергии продуктов и исходных веществ. Если этот относительный запас энергии измерен при постоянном давлении, он называется энтальпией. Направление, в котором самопроизвольно протекает химическая реакция, определяется совместным действием двух факторов: 1) тенденцией к переходу системы в состояние с наименьшей внутренней энергией (с наименьшей энтальпией); 2) тенденцией к достижению более вероятного состояния, перехода из более упорядоченного состояния в менее упорядоченное (с наибольшей энтальпией). Энтропия является количественной мерой беспорядка в системе.

Изменение энергии Гиббса одновременно учитывает изменение энергетического запаса системы и степени ее беспорядка.

∆G = ∆– T∆S

Таким образом, чем отрицательнее величина ∆H, тем больше отрицательная величина ∆G. И чем положительнее величина ∆S, тем больше отрицательна величина ∆G. Рассмотрение приведенного уравнения зависимости ∆G реакции от ∆H и ∆S приводит к следующим выводам:

1. если ∆H < 0 и ∆S > 0, то ∆G < 0, т.е. экзотермическая реакция с увеличением энтропии в системе возможна при всех температурах;

2. если ∆H > 0, а ∆S < 0, то ∆G > 0, т.е. эндотермическая реакция с уменьшением энтропии в системе невозможна ни при каких температурах;

3. если ∆H < 0 и ∆S < 0 или ∆H > 0 и ∆S > 0, то знак при ∆G зависит от соотношения величин ∆и T∆S, но реакция возможна только в случае ∆G < 0.

4. 4MnO₂ = 2Mn₂O₃ + O₂ (1) ∆ = -212,55 кДж

6Mn₂O₃ = 4Mn₃O₄ + O₂ (2) ∆ = -156,94 кДж

Утроим первой уравнение реакции и сложим его со вторым. Получим:

12MnO₂ + 6Mn₂O₃ = 6Mn₂O₃ + 3O₂ + O₂ + 4Mn₃O₄

Сократим 6Mn₂O₃ в левой и правой частях этого уравнения, а коэффициенты перед оставшимися веществами сократим на 4. Получим:

3 MnO₂ = Mn₃O₄ + O₂

∆ = 3*∆H₁ + ∆H₂ = 3*(-212,55) + (-156,94) = -794,59 кДж

Ответ: ∆ = -794,59 кДж

4. 1. 2NO + O₂ = 2NO₂ ∆= -112,6 кДж

Первоначальные скорости прямой и обратной реакции были следующие:

υ_пр = K₁**; υ_обр = K₂*

При увеличении давления в два раза концентрация всех реагирующих веществ увеличилась в два раза, так как общий объем системы уменьшился в два раза. Тогда скорость прямой реакции:

υ = K₁*(2)²*2 = 8 K₁**

т.е. возросла в восемь раз. А скорость обратной реакции:

υ= K₂*(2)² = 4 K₂*

т.е. возросла в четыре раза. Следовательно, равновесие сместится в сторону прямой реакции.

2. N₂ + 3H₂ = 2NH₃ ∆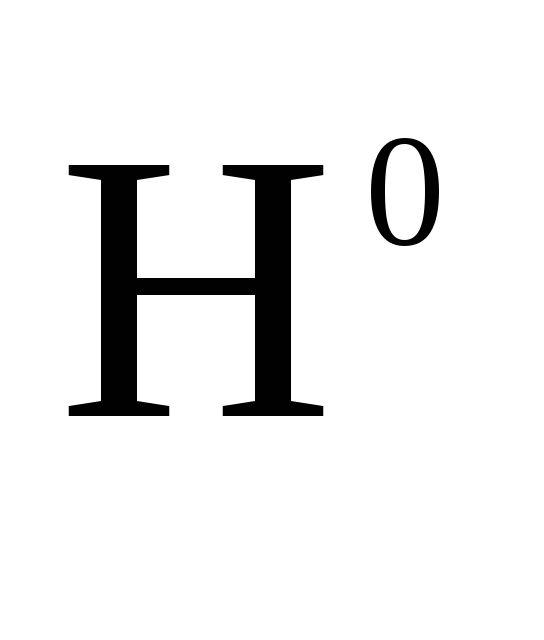= -92,38 кДж

υ_пр = K₁**; υ_обр = K₂*

После увеличения давления в два раза:

υ = K₁*2*(2)³ = 16 K₁**

т.е. скорость прямой реакции возрастает в шестнадцать раз.

υ= K₂*(2)² = 4 K₂*

т.е. скорость обратной реакции возрастает в четыре раза. Следовательно, равновесие сместится в сторону прямой реакции.

3. 2H₂ + O₂ = 2H₂O_(пар) ∆= -483,58 кДж

υ_пр = K₁**; υ_обр = K₂*

После увеличения давления в два раза:

υ = K₁*(2)²*2= 8 K₁**

т.е. скорость прямой реакции возросла в восемь раз.

υ= K₂*(2)² = 4 K₂*

т.е. скорость обратной реакции возросла в четыре раза. Следовательно, равновесие сместится в сторону прямой реакции.

4. В соответствии с правилом Вант-Гоффа

υ= υ* γ

T₂ – T₁ = 25

υ/ υ = γ = 2,3 = 2,3^2,5 = = (2,3)² * = 8,023

Скорость реакции возрастет в 8,023 раза.

4. Данному заданию соответствует диаграмма плавкости твердого раствора. Характерной особенностью подобной системы является то, что температура плавления твердого раствора данного состава не совпадает с температурой затвердевания жидкого раствора (расплава) того же состава. Поэтому на диаграмме плавкости наблюдаются две кривые: верхняя отражает температуры затвердевания расплава (линия ликвидуса), нижняя – температуры плавления твердого раствора (линия солидуса).

Построим диаграмму системы медь-никель (Cu-Ni) и кривые охлаждения расплавов содержащих 0, 40, 100% никеля.

3-3 кривая охлаждения расплава содержащего 0% никеля;

2-2 кривая охлаждения расплава содержащего 40% никеля;

1-1 кривая охлаждения расплава содержащего 100% никеля.

Для любой области и точки на диаграмме плавкости применимо правило фаз Гиббса:

С = К + 2 – Ф

Так как мы строили диаграммы плавкости в координатах состав-температура, следовательно: С = К + 1 – Ф

Таким образом, для области 4: К = 2, Ф = 1, С = 2 + 1 – 1 = 2;

для области 5: К = 2, Ф = 3, С = 2 + 1 – 3 = 0;

для области 6: К = 2, Ф = 1, С = 2 + 1 – 1 = 2;

на линии ликвидуса: К = 2, Ф = 3, С = 2 + 1 – 3 = 0;

на линии солидуса: К = 2, Ф = 3, С = 2 + 1 – 3 = 0;

в точке А: К = 1, Ф = 1, С = 1 + 1 – 1 = 1;

в точке Д: К = 2, Ф = 2, С = 2 + 1 – 2 = 1.

Твердыми растворами называют фазы переменного состава, находящиеся в состоянии химического (термодинамического) равновесия. По механизму образования твердые растворы можно подразделить на следующие основные типы: замещения, внедрения, вычитания.

1. Твердые растворы замещения возникают в результате статистического замещения одних частиц другими в узлах кристаллической решетки растворителя. Это единственный случай при образовании твердых растворов, когда возможна полная взаимная растворимость. Например, при постепенном замещении атомов натрия в кристаллической решетке NaCl атомами калия, можно непрерывно перейти от одного чистого компонента (NaCl) к другому (KCl). Непрерывный ряд твердых растворов замещения может образоваться при значительном сходстве физико-химического характера компонента. Если же сочетание факторов, определяющих растворимость, не очень благоприятно, то наблюдается ограниченная взаимная растворимость. Обычно различают твердые растворы с катионным (Na_xK_1-xCl) и анионным (KCl_xBr_1-x) замещением. Кроме того, следует различать изовалентное и гетеровалентное замещение. При изовалентном замещении атомы растворяемого вещества и растворителя имеют одинаковую валентность (AlSB – GaSb, KCl – KBr и т.п.). Гетеровалентное замещение наблюдается при разной валентности атомов растворителя и растворенного вещества. Так, твердые растворы Ga₂Se₃ – GaAs представляют собой пример твердых растворов с анионным гетеровалентным замещением. Встречаются более сложные варианты образования растворов замещения, когда одновременно наблюдается и катионно-анионное, и гетеровалентное замещение. Например, в системе KMnO₄ – BaSO₄, в катионной и анионной подрешетках осуществляется гетеровалентное замещение.

2. Твердые растворы внедрения образуются в результате встраивания атомов растворяемого вещества в междоузлия кристаллической решетки растворителя. Растворы такого типа могут быть только ограниченными. Размер внедряемого атома должен быть небольшим и оптимально соответствовать объему пустот в междоузлиях кристаллической решетки растворителя. При образовании металлических твердых растворов внедрения в качестве внедряемых атомов обычно выступают легкие неметаллы, обладающие малым радиусом: H, B, C, N, O. При этом встраивание их в пустоты решетки существенным образом не влияет на характер взаимодействия атомов и не изменяет типа кристаллической решетки. Например, твердые растворы водорода в титане и палладии, бора в переходных металлах обладают металлическими свойствами, поскольку внедрение атомов водорода и бора в кристаллические структуры соответствующих металлов, во-первых, не нарушает общего металлического характера взаимодействия атомов, а во-вторых, электроны внедряемых атомов также обобществляются.

3. Твердые растворы вычитания образуются только на основе химических соединений при недостатке одного из компонентов в соответствующей подрешетке. Типичный пример твердого раствора вычитания представляет собой фаза TiO, состав которой характеризуется формулой Ti_0,75-1,00O_1,00-0,58. Реально эта фаза существует как в виде твердого раствора вычитания по титану Ti_0,75-1,00O (вакантна часть мест в подрешетке титана), так и в виде твердого раствора вычитания по кислороду TiO_1,00-0,58 (все места в подрешетке титана заняты, а часть кислородных вакантна). Твердые растворы вычитания, как и растворы внедрения, могут быть только ограниченными.

8. 1) 2Fe₃O_4(T) = 6FeO_(T) + O_2(Г)

1. Fe₃O_4(T) = 3Fe_(T) + 2O_2(Г)

2. 2FeO_(T) = 2Fe_(T) + O_2(Г)

Число степеней свободы можно выразить как разность между общим числом переменных и числом уравнений: C = K + 2 – f

В нашей системе четыре составляющих вещества: Fe_(T), Fe₃O_4(T), FeO_(T), O_2(Г), но три независимых компонента, так как концентрация вещества в газовой фазе определяется константой равновесия. Число фаз четыре (три кристаллических и одна газообразная). Следовательно, С = 3 + 2 – 4 = 1. Т.е. система имеет одну степень свободы: каждой температуре соответствует определенная концентрация (или давление) O₂.