Лабораторная работа 3
Определение ускорения свободного падения с помощью универсального маятника
ЦЕЛЬ РАБОТЫ
1. Изучить математический, физический и оборотный маятники и связанные с ним основные физические понятия и законы.
2. Научиться экспериментально определять ускорение свободного падения с помощью этих маятников.
3. Научиться экспериментально определять момент инерции тела относительно произвольной оси вращения.
Математический маятник
КРАТКАЯ ТЕОРИЯ
Математическим маятником называется идеализированная система, состоящая из материальной точки массой m и невесомой недеформируемой нити длиной l. (рис.1). Колебательным движением (колебанием) называется процесс, при котором система, многократно отклоняясь от своего состояния равновесия, каждый раз вновь возвращается к нему. Если этот возврат совершается через равные промежутки времени Т, то колебание называется периодическим, а Т – периодом колебаний. Наглядным примером периодического колебания служит движение часового маятника.
Периодическое колебание, при котором смещение х меняется со временем по закону синуса или косинуса, называется гармоническим колебанием.
х
= Аsin
(1) где
- круговая частота,
А – максимальная амплитуда колебаний,
t – текущее время.
Скорость
колебания материальной точки
определяется как производная смещения
(1) по времени
(2)
Из
уравнения (2) видно, что скорость колебания
изменяется со временем. Следовательно,
колебательное движение совершается с
ускорением а,
которое можно определить, продифференцировав
выражение скорости
а
=
(3) или учитывая формулу
(1)
а
=
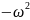х.
(4)
Математический маятник при малых отклонениях (4-50) совершает гармонические колебания. При отклонении маятника на величину х на маятник начинает действовать возвращающая сила F, которая обусловлена силой тяжести Q. Из рис. 1 видно, что
F
=
Q
sinα
= -mgsin
Знак
минус обусловлен тем, что направления
силы и угла отклонения всегда
противоположны. При малых отклонениях
х sinα
,
поэтому sinα
. Тогда
F
=
mgα
=
mg
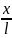. (5) В соответствии со
вторым законом Ньютона возвращающая
сила выразится соотношением
F
= ma
.
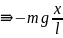Получим а = - g .
Учитывая формулу (4) напишем соотношение, откуда найдем выражения круговой частоты и периода колебаний математического маятника
,
(6)
.
(7)
Из формулы (7) следует, что при малых отклонениях а период колебания математического маятника пропорционален квадратному корню из длины маятника, обратно пропорционален квадратному корню из ускорения свободного падения и не зависит от амплитуды колебаний и массы маятника. Из формулы (7), зная Т и l, можно определить g – величину ускорения свободного падения тела. Поскольку Земля является не точным шаром, а эллипсоидом, несколько сплюснутым у полюсов, и, кроме того, на тела действуют центробежные силы, особенно заметные на экваторе, то величина g зависит от географической широты и на полюсе несколько больше, чем на экваторе.
-
Положение точки географическая широта м/с2
Полюс 900 9,832
Москва 530 9,815
Пермь 580 9,8275
Экватор 00 9,780
Эксперимент по определению ускорения свободного падения произвести по инструкции, представленной в упражнении №1 на установке FРМ-04.