
- •2)Задача про шлях точки у прямолінійному русі.
- •Означення визначеного інтеграла. Геометричний і фізичний зміст визначеного інтеграла.
- •Основні властивості визначеного інтеграла.
- •Формула Ньютона-Лейбніца
- •Обчислення визначеного інтеграла. Інтегрування підстановкою (заміни змінної).
- •Теорема. Якщо:
- •Обчислення визначеного інтеграла. Інтегрування частинами.
- •Інтегрування парних і непарних функцій в симетричних межах.
- •В першому інтегралі зробимо підстановку . Тоді
- •Наближене обчислення визначених інтегралів
- •Метод прямокутників
- •М етод трапецій
- •Метод парабол (формула Сімпсона)
Лекція 20
Тема: Визначений інтеграл
Задачі, що приводять до поняття визначеного інтеграла.
Задача про площу криволінійної трапеції.

Нехай
на відрізку
 задана невід’ємна обмежена функція
задана невід’ємна обмежена функція
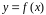 .
Потрібно знайти площу фігури, обмеженої
графіком функції
,
прямими
.
Потрібно знайти площу фігури, обмеженої
графіком функції
,
прямими

 і віссю абсцис
і віссю абсцис
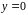 (рис.1) Таку фігуру називають криволінійною
трапецією.
(рис.1) Таку фігуру називають криволінійною
трапецією.
З
Рис. 1
цією метою розіб’ємо відрізок на будь-яке число частин (відрізків) точками
частин (відрізків) точками
Довжину
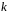 -ого
частинного відрізка позначимо
-ого
частинного відрізка позначимо

 ,
на кожному частинному відрізку оберемо
по одній точці
,
на кожному частинному відрізку оберемо
по одній точці
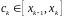 ,
,
 .
В точці
.
В точці
 проведемо перпендикуляр до осі
проведемо перпендикуляр до осі
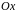 до зустрічі з кривою
,
через точку зустрічі проведемо пряму,
паралельну осі
до зустрічі з прямими
до зустрічі з кривою
,
через точку зустрічі проведемо пряму,
паралельну осі
до зустрічі з прямими
 і
і
 .
Так на кожному частинному відрізку
буде побудовано прямокутник з основою
.
Так на кожному частинному відрізку
буде побудовано прямокутник з основою
 ,
висотою
,
висотою
 і, отже площею
і, отже площею
 .
Сукупність цих прямокутників утворює
ступінчату фігуру, яка при достатньо
дрібному розбитті буде як завгодно
мало відрізнятися від заданої криволінійної
трапеції. Тоді площа ступінчатої фігури,
яка дорівнює сумі площ прямокутників,
що її складають, наближено дорівнюватиме
площі
.
Сукупність цих прямокутників утворює
ступінчату фігуру, яка при достатньо
дрібному розбитті буде як завгодно
мало відрізнятися від заданої криволінійної
трапеції. Тоді площа ступінчатої фігури,
яка дорівнює сумі площ прямокутників,
що її складають, наближено дорівнюватиме
площі
 криволінійної трапеції:
криволінійної трапеції:
 .
.
Ці
рівність тим точніша, чим дрібнішим є
розбиття проміжку
,
і природно за площу криволінійної
трапеції вважати границю площ ступінчатих
фігур за умови необмеженого подрібнення
розбиття, тобто при
 :
:
 .
.
2)Задача про шлях точки у прямолінійному русі.
Нехай
точка рухається по прямій з швидкістю
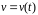 .
Потрібно знайти шлях, пройдений точкою
за проміжок часу
.
Потрібно знайти шлях, пройдений точкою
за проміжок часу
 ,
тобто від моменту
,
тобто від моменту
 до моменту
до моменту
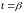 .
.
Розіб’ємо
проміжок часу від
 до
до
 на
частинних проміжків часу моментами
на
частинних проміжків часу моментами
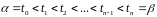 .
.
Тривалість
-го
часового проміжку позначимо
 і в кожному такому проміжку оберемо по
одному значенню
і в кожному такому проміжку оберемо по
одному значенню

 .
Якщо розбиття проміжку
.
Якщо розбиття проміжку
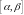 достатньо дрібне, то швидкість точки
на
-ому
частинному проміжку можна наближено
вважати сталою, рівною
достатньо дрібне, то швидкість точки
на
-ому
частинному проміжку можна наближено
вважати сталою, рівною
 , а шлях, пройдений за цей проміжок часу
, наближено рівним
, а шлях, пройдений за цей проміжок часу
, наближено рівним
 .
Сума цих «частинних» шляхів дасть
наближене значення всього шляху
.
Сума цих «частинних» шляхів дасть
наближене значення всього шляху
 ,
пройденого точкою за проміжок часу
:
,
пройденого точкою за проміжок часу
:
 .
.
Точність
цієї формули збільшується із зменшенням
усіх величин
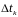 ,
,
отже
при необмеженому подрібненні розбиття,
тобто при переході до границі при
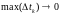 ,
отримуємо
,
отримуємо
 .
.
Означення визначеного інтеграла. Геометричний і фізичний зміст визначеного інтеграла.
В попередньому пункті розглянуто дві задачі, взяті з різних галузей знання – одну з геометрії, іншу з фізики. Якщо абстрагуватися від конкретного змісту цих задач і зосередити увагу на їх аналітичній структурі, то бачимо , що в цьому сенсі вони цілком однакові. В обох випадках розв’язання задачі вимагає обчислення границі деякої суми цілком певної будови. Таку ж аналітичну структуру має величезна кількість задач, які виникають у різних галузях науки, техніки, економіки і взагалі людської діяльності. Виникає потреба у створенні спеціального математичного апарату для розв’язання подібних задач. Таким апаратом є визначений інтеграл.
Означення. Нехай на відрізку задана обмежена функція . Розіб’ємо відрізок на частинних відрізків точками
 .
.
На
кожному відрізку
 розбиття візьмемо довільно точку
і позначимо
,
де
розбиття візьмемо довільно точку
і позначимо
,
де
 .
Побудуємо суму
.
Побудуємо суму
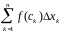 ,
яку будемо називати інтегральною
сумою
для функції
,
яку будемо називати інтегральною
сумою
для функції
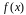 на відрізку
.
Очевидно, що інтегральна сума залежить
від способу розбиття відрізка
і від вибору проміжних точок
.
на відрізку
.
Очевидно, що інтегральна сума залежить
від способу розбиття відрізка
і від вибору проміжних точок
.
Якщо
існує скінченна границя інтегральної
суми при
 (тобто при необмеженому подрібненні
розбиття відрізка
)
і ця границя не залежить ні від способу
розбиття, ні від вибору проміжних точок
,
то ця границя називається визначеним
інтегралом функції
на відрізку
і позначається
(тобто при необмеженому подрібненні
розбиття відрізка
)
і ця границя не залежить ні від способу
розбиття, ні від вибору проміжних точок
,
то ця границя називається визначеним
інтегралом функції
на відрізку
і позначається
 .
.
Тоді
функція
називається інтегровною
на відрізку
,
числа
 і
і
 називаються відповідно нижньою
і верхньою межами
інтегрування,
відрізок
- проміжком
інтегрування.
називаються відповідно нижньою
і верхньою межами
інтегрування,
відрізок
- проміжком
інтегрування.
Повертаючись до задач попереднього пункту , доходимо висновку, що
а)
площа
криволінійної трапеції, обмеженої
прямими
,
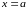 ,
і графіком функції
,
і графіком функції
 ,
дорівнює визначеному інтегралу від
цієї функції:
,
дорівнює визначеному інтегралу від
цієї функції:
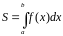 (геометричний
зміст визначеного інтеграла);
якщо
(геометричний
зміст визначеного інтеграла);
якщо
 ,
то отримуємо відповідну площу із знаком
мінус;
,
то отримуємо відповідну площу із знаком
мінус;
б)
шлях
,
пройдений точкою за проміжок часу від
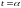 до
до
 , дорівнює визначеному інтегралу від
швидкості
, дорівнює визначеному інтегралу від
швидкості
 :
:
 (фізичний
зміст визначеного інтеграла).
(фізичний
зміст визначеного інтеграла).
Зауважимо,
що визначений інтеграл є числом,
яке не залежить від позначення змінної
інтегрування, тобто
 і т.д.
і т.д.
Виникає питання про умови, при яких визначений інтеграл існує.
Теорема
(достатня
умова існування визначеного інтеграла).
Якщо функція
неперервна на відрізку
,
то вона інтегровна на цьому відрізку,
тобто інтеграл
 існує.
існує.
Ця умова є лише достатньою, тобто інтегровними можуть бути і деякі функції з точками розриву на проміжку інтегрування, але ми в подальшому вважатимемо підінтегральні функції неперервними, якщо не обумовлено протилежне.
