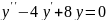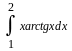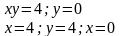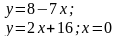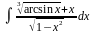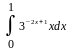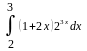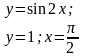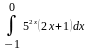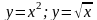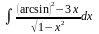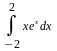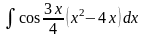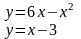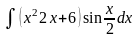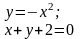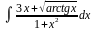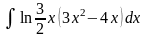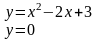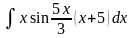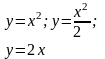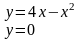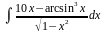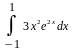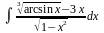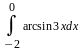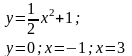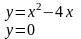- •Практическая работа №4 Тема: «Нахождение производных и дифференциалов функции. Приложения производных и дифференциалов»
- •Практическая работа №4 Тема: «Нахождение производных и дифференциалов функции. Приложения производных и дифференциалов»
- •Практическая работа №4 Тема: «Нахождение производных и дифференциалов функции. Приложения производных и дифференциалов»
- •Практическая работа №4 Тема: «Нахождение производных и дифференциалов функции. Приложения производных и дифференциалов»
- •Практическая работа №4 Тема: «Нахождение производных и дифференциалов функции. Приложения производных и дифференциалов»
- •Практическая работа №4 Тема: «Нахождение производных и дифференциалов функции. Приложения производных и дифференциалов»
- •Практическая работа №4 Тема: «Нахождение производных и дифференциалов функции. Приложения производных и дифференциалов»
- •Практическая работа №4 Тема: «Нахождение производных и дифференциалов функции. Приложения производных и дифференциалов»
- •Практическая работа №4 Тема: «Нахождение производных и дифференциалов функции. Приложения производных и дифференциалов»
- •Практическая работа №4 Тема: «Нахождение производных и дифференциалов функции. Приложения производных и дифференциалов»
- •Практическая работа №4 Тема: «Нахождение производных и дифференциалов функции. Приложения производных и дифференциалов»
- •Практическая работа №4 Тема: «Нахождение производных и дифференциалов функции. Приложения производных и дифференциалов»
- •Практическая работа №4 Тема: «Нахождение производных и дифференциалов функции. Приложения производных и дифференциалов»
- •Практическая работа №4 Тема: «Нахождение производных и дифференциалов функции. Приложения производных и дифференциалов»
- •Практическая работа №4 Тема: «Нахождение производных и дифференциалов функции. Приложения производных и дифференциалов»
- •Практическая работа №4 Тема: «Нахождение производных и дифференциалов функции. Приложения производных и дифференциалов»
- •Практическая работа №4 Тема: «Нахождение производных и дифференциалов функции. Приложения производных и дифференциалов»
- •Практическая работа №4 Тема: «Нахождение производных и дифференциалов функции. Приложения производных и дифференциалов»
- •Практическая работа №4 Тема: «Нахождение производных и дифференциалов функции. Приложения производных и дифференциалов»
- •Практическая работа Тема: «Нахождение производных и дифференциалов функции. Приложения производных и дифференциалов»
- •Практическая работа №4 Тема: «Нахождение производных и дифференциалов функции. Приложения производных и дифференциалов»
- •Практическая работа №4 Тема: «Нахождение производных и дифференциалов функции. Приложения производных и дифференциалов»
- •Практическая работа №4 Тема: «Нахождение производных и дифференциалов функции. Приложения производных и дифференциалов»
- •Практическая работа №4 Тема: «Нахождение производных и дифференциалов функции. Приложения производных и дифференциалов»
- •Практическая работа №4 Тема: «Нахождение производных и дифференциалов функции. Приложения производных и дифференциалов»
- •Практическая работа №4 Тема: «Нахождение производных и дифференциалов функции. Приложения производных и дифференциалов»
- •Практическая работа №4 Тема: «Нахождение производных и дифференциалов функции. Приложения производных и дифференциалов»
- •Практическая работа №4 Тема: «Нахождение производных и дифференциалов функции. Приложения производных и дифференциалов»
- •Практическая работа №4 Тема: «Нахождение производных и дифференциалов функции. Приложения производных и дифференциалов»
- •Практическая работа №4 Тема: «Нахождение производных и дифференциалов функции. Приложения производных и дифференциалов»
- •Практическая работа №5 Тема «Вычисление интегралов. Приложения интегралов»
- •Практическая работа №6 Тема: «Решение дифференциальных уравнений»
- •Практическая работа №6 Тема: «Решение дифференциальных уравнений»
- •Практическая работа №6 Тема: «Решение дифференциальных уравнений»
- •Практическая работа №6 Тема: «Решение дифференциальных уравнений»
- •Практическая работа №6 Тема: «Решение дифференциальных уравнений»
- •Практическая работа №6 Тема: «Решение дифференциальных уравнений»
- •Практическая работа №6 Тема: «Решение дифференциальных уравнений»
- •Практическая работа №6 Тема: «Решение дифференциальных уравнений»
- •Практическая работа №6 Тема: «Решение дифференциальных уравнений»
- •Практическая работа №6 Тема: «Решение дифференциальных уравнений»
- •Практическая работа №6 Тема: «Решение дифференциальных уравнений»
- •Практическая работа №6 Тема: «Решение дифференциальных уравнений»
- •Практическая работа №6 Тема: «Решение дифференциальных уравнений»
- •Практическая работа №6 Тема: «Решение дифференциальных уравнений»
- •Практическая работа №6 Тема: «Решение дифференциальных уравнений»
- •Практическая работа №6 Тема: «Решение дифференциальных уравнений»
- •Практическая работа №6 Тема: «Решение дифференциальных уравнений»
- •Практическая работа №6 Тема: «Решение дифференциальных уравнений»
- •Практическая работа №6 Тема: «Решение дифференциальных уравнений»
- •Практическая работа №6 Тема: «Решение дифференциальных уравнений»
- •Практическая работа №6 Тема: «Решение дифференциальных уравнений»
- •Практическая работа №6 Тема: «Решение дифференциальных уравнений»
- •Практическая работа №6 Тема: «Решение дифференциальных уравнений»
- •Практическая работа №6 Тема: «Решение дифференциальных уравнений»
- •Практическая работа №6 Тема: «Решение дифференциальных уравнений»
- •Практическая работа №6 Тема: «Решение дифференциальных уравнений»
- •Практическая работа №6 Тема: «Решение дифференциальных уравнений»
- •Практическая работа №6 Тема: «Решение дифференциальных уравнений»
- •Практическая работа №6 Тема: «Решение дифференциальных уравнений»
- •Практическая работа №6 Тема: «Решение дифференциальных уравнений»
- •Практическая работа № 8 Тема: «Нахождение вероятности событий. Вычисление числовых характеристик дискретной случайной величины»
- •Практическая работа № 8 Тема: «Нахождение вероятности событий. Вычисление числовых характеристик дискретной случайной величины»
- •Практическая работа № 8 Тема: «Нахождение вероятности событий. Вычисление числовых характеристик дискретной случайной величины»
- •Практическая работа № 8 Тема: «Нахождение вероятности событий. Вычисление числовых характеристик дискретной случайной величины»
- •Практическая работа № 8 Тема: «Нахождение вероятности событий. Вычисление числовых характеристик дискретной случайной величины»
- •Практическая работа № 8 Тема: «Нахождение вероятности событий. Вычисление числовых характеристик дискретной случайной величины»
- •Практическая работа № 8 Тема: «Нахождение вероятности событий. Вычисление числовых характеристик дискретной случайной величины»
- •Практическая работа № 8 Тема: «Нахождение вероятности событий. Вычисление числовых характеристик дискретной случайной величины»
- •Практическая работа № 8 Тема: «Нахождение вероятности событий. Вычисление числовых характеристик дискретной случайной величины»
- •Практическая работа № 8 Тема: «Нахождение вероятности событий. Вычисление числовых характеристик дискретной случайной величины»
- •Практическая работа №8 Тема: «Нахождение вероятности событий. Вычисление числовых характеристик дискретной случайной величины»
- •Практическая работа № 8 Тема: «Нахождение вероятности событий. Вычисление числовых характеристик дискретной случайной величины»
- •Практическая работа № 8 Тема: «Нахождение вероятности событий. Вычисление числовых характеристик дискретной случайной величины»
- •Практическая работа №8 Тема: «Нахождение вероятности событий. Вычисление числовых характеристик дискретной случайной величины»
- •Практическая работа № 8 Тема: «Нахождение вероятности событий. Вычисление числовых характеристик дискретной случайной величины»
- •Практическая работа № 8 Тема: «Нахождение вероятности событий. Вычисление числовых характеристик дискретной случайной величины»
- •Практическая работа № 8 Тема: «Нахождение вероятности событий. Вычисление числовых характеристик дискретной случайной величины»
- •Практическая работа № 8 Тема: «Нахождение вероятности событий. Вычисление числовых характеристик дискретной случайной величины»
- •Практическая работа № 8 Тема: «Нахождение вероятности событий. Вычисление числовых характеристик дискретной случайной величины»
- •Практическая работа № 8 Тема: «Нахождение вероятности событий. Вычисление числовых характеристик дискретной случайной величины»
- •Практическая работа №8 Тема: «Нахождение вероятности событий. Вычисление числовых характеристик дискретной случайной величины»
- •Практическая работа № 8 Тема: «Нахождение вероятности событий. Вычисление числовых характеристик дискретной случайной величины»
- •Практическая работа № 8 Тема: «Нахождение вероятности событий. Вычисление числовых характеристик дискретной случайной величины»
- •Практическая работа № 8 Тема: «Нахождение вероятности событий. Вычисление числовых характеристик дискретной случайной величины»
- •Практическая работа № 8 Тема: «Нахождение вероятности событий. Вычисление числовых характеристик дискретной случайной величины»
- •Практическая работа № 8 Тема: «Нахождение вероятности событий. Вычисление числовых характеристик дискретной случайной величины»
- •Практическая работа № 8 Тема: «Нахождение вероятности событий. Вычисление числовых характеристик дискретной случайной величины»
- •Практическая работа № 8 Тема: «Нахождение вероятности событий. Вычисление числовых характеристик дискретной случайной величины»
- •Практическая работа № 8 Тема: «Нахождение вероятности событий. Вычисление числовых характеристик дискретной случайной величины»
- •Практическая работа №9 Тема: «Обработка статистических данных» Вариант- 1
- •Практическая работа №9 Тема: «Обработка статистических данных» Вариант- 2
- •Практическая работа №9 Тема: «Обработка статистических данных» Вариант- 3
- •Практическая работа №9 Тема: «Обработка статистических данных» Вариант- 4
- •Практическая работа №9 Тема: «Обработка статистических данных» Вариант- 5
- •Практическая работа №9 Тема: «Обработка статистических данных» Вариант- 6
- •Практическая работа №9 Тема: «Обработка статистических данных» Вариант- 7
- •Практическая работа №9 Тема: «Обработка статистических данных» Вариант- 8
- •Практическая работа №9 Тема: «Обработка статистических данных» Вариант- 9
- •Практическая работа №9 Тема: «Обработка статистических данных» Вариант- 10
- •Практическая работа №9 Тема: «Обработка статистических данных» Вариант- 11
- •Практическая работа №9 Тема: «Обработка статистических данных» Вариант- 12
- •Практическая работа №9 Тема: «Обработка статистических данных» Вариант- 13
- •Практическая работа №9 Тема: «Обработка статистических данных» Вариант- 14
- •Практическая работа №9 Тема: «Обработка статистических данных» Вариант- 15
- •Практическая работа №9 Тема: «Обработка статистических данных» Вариант- 16
- •Практическая работа №9 Тема: «Обработка статистических данных» Вариант- 17
- •Практическая работа №9 Тема: «Обработка статистических данных» Вариант- 18
- •Практическая работа №9 Тема: «Обработка статистических данных» Вариант- 19
- •Практическая работа №9 Тема: «Обработка статистических данных» Вариант- 20
- •Практическая работа №9 Тема: «Обработка статистических данных» Вариант- 21
- •Практическая работа №9 Тема: «Обработка статистических данных» Вариант- 22
- •Практическая работа №9 Тема: «Обработка статистических данных» Вариант- 23
- •Практическая работа №9 Тема: «Обработка статистических данных» Вариант- 24
- •Практическая работа №9 Тема: «Обработка статистических данных» Вариант- 25
- •Практическая работа №9 Тема: «Обработка статистических данных» Вариант- 26
- •Практическая работа №9 Тема: «Обработка статистических данных» Вариант- 27
- •Практическая работа №9 Тема: «Обработка статистических данных» Вариант- 28
- •Практическая работа №9 Тема: «Обработка статистических данных» Вариант- 29
- •Практическая работа №9 Тема: «Обработка статистических данных» Вариант- 30
Практическая работа №5 Тема «Вычисление интегралов. Приложения интегралов»
|
Вычислить неопределенные и определенные интегралы, применяя подходящие подстановки |
Вычислить площадь фигуры, ограниченной линиями |
|
|||||
|
1 |
|
3
|
4 |
5 |
6 |
||
1 |
|
|
|
|
|
Составить и решить две прикладные задачи с использованием определенных и неопределенных интегралов |
||
2 |
|
|
|
|
|
|||
3 |
|
|
|
|
|
|||
4 |
|
|
|
|
|
|||
5 |
|
|
|
|
|
|||
6 |
|
|
|
|
|
|||
7 |
|
|
|
|
|
|||
8 |
|
|
|
|
|
|||
9 |
|
|
|
|
|
|||
10 |
|
|
|
|
|
|||
Практическая работа №6 Тема: «Решение дифференциальных уравнений»
Вариант- 1
Какие из приведенных дифференциальных уравнений являются дифференциальными уравнениями 1-го порядка с разделенными переменными:
а)
(x-1) dy=(y+1)dx
b) d S=(
 c)
c)

Найти функцию, если известна ее производная и координаты точки, принадлежащей этой функции
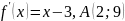
Решите уравнение:

Найти частное решение дифференциального уравнения:
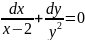 ,
,
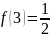
Найти общее решение дифференциального уравнения:

Решить задачу Коши для ЛДУ1-го порядка:

Найти общее решение дифференциального уравнения:
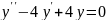
Практическая работа №6 Тема: «Решение дифференциальных уравнений»
Вариант- 2
Какие из приведенных дифференциальных уравнений являются дифференциальными уравнениями 1-го порядка с разделенными переменными:
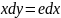 b)
b)
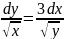 c)
c)
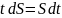
Найти функцию, если известна ее производная и координаты точки, принадлежащей этой функции
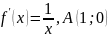
Решите уравнение:

Найти частное решение дифференциального уравнения:
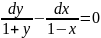 ,
,

Найти общее решение дифференциального уравнения:

Решить задачу Коши для ЛДУ1-го порядка:
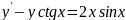 ,
,
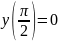
Найти общее решение дифференциального уравнения:
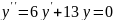
Практическая работа №6 Тема: «Решение дифференциальных уравнений»
Вариант- 3
Какие из приведенных дифференциальных уравнений являются дифференциальными уравнениями 1-го порядка с разделенными переменными:
a)
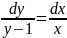 b)
b)
 c)
c)

Найти функцию, если известна ее производная и координаты точки, принадлежащей этой функции
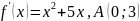
Решите уравнение:

Найти частное решение дифференциального уравнения:
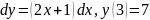
Найти общее решение дифференциального уравнения:

Решить задачу Коши для ЛДУ1-го порядка:
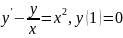
Найти общее решение дифференциального уравнения: