Федеральное Агентство по образованию

ТОМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ СИСТЕМ УПРАВЛЕНИЯ И РАДИОЭЛЕКТРОНИКИ (ТУСУР)

Кафедра физики

ОТЧЕТ

Лабораторная работа по курсу "Общая физика"

ОПРЕДЕЛЕНИЕ ШИРИНЫ ЗАПРЕЩЕННОЙ ЗОНЫ ПОЛУПРОВОДНИКА ПО ТЕМПЕРАТУРНОЙ ЗАВИСИМОСТИ ОБРАТНОГО ТОКА ДИОДА

Выполнил студент

_____________________

2009

1. ЦЕЛЬ РАБОТЫ

Целью работы является исследование температурной зависимости обратного тока диода и определение ширины запрещенной зоны полупроводника.

2. ОПИСАНИЕ УСТАНОВКИ И МЕТОДИКИ ЭКСПЕРИМЕНТА

Э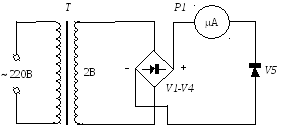 кспериментальная установка состоит из нагревателя, в котором находится германиевый диод, термометра для измерения температуры и электрической схемы. Электрическая схема включения диода представлена на рис. 2.1. Она состоит из понижающего трансформатора Т, выпрямителя V1-V4 и микроамперметра P1 для измерения тока через исследуемый диод V5.

Рисунок 2.1 - Электрическая схема экспериментальной установки.

3. ОСНОВНЫЕ РАСЧЕТНЫЕ ФОРМУЛЫ

Экспериментальное значение ширины запрещенной зоны (в Дж)

Е = a k, (3.1)

где k - постоянная Больцмана;

a - угловой коэффициент линеаризованного графика lnI_обр = f(1/T), который находится по формуле:

(3.2)

Параметры линейной зависимости a и b, определяем аналитическим способом по методу наименьших квадратов (МНК):

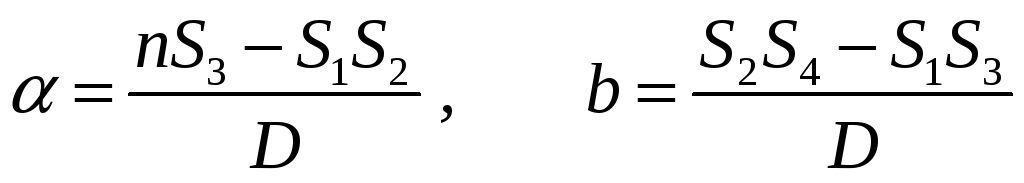
(3.3)

где обозначено:

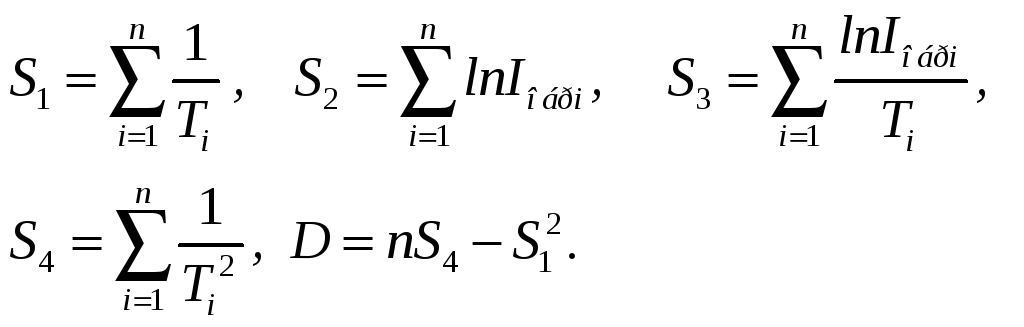
(3.4)

В этих формулах n – число экспериментальных точек, а наборы чисел (1/T) и (lnI_обр) – результаты измерений, то есть абсциссы и ординаты экспериментальных точек.

Абсолютная погрешность косвенного измерения величины lnI_обр равна:

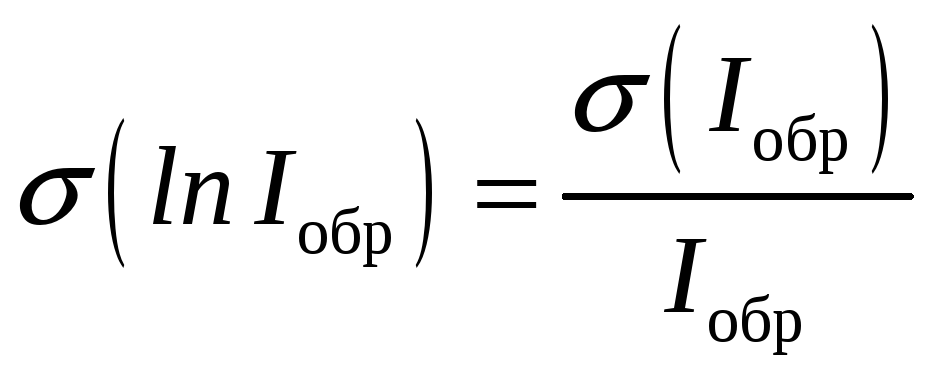
(величина безразмерная) (3.5)

Абсолютная приборная погрешность прямого измерения обратного тока диода I_обр цифровым прибором равна:

1 В младшем разряде прибора (3.5а)

Абсолютная погрешность косвенного измерения величины 1/Т равна:

(3.6)

Абсолютная приборная погрешность прямого измерения температуры диода принимается равной половине цены наименьшего деления термометра:

(T) = 0,5 K (3.6a)

Абсолютная погрешность экспериментального значения ширины запрещенной зоны на основании выражения 3.1:

(Е) = (а)×k (3.7)

где (a) - погрешность углового коэффициента (a) определяется по специальным формулам метода наименьших квадратов :

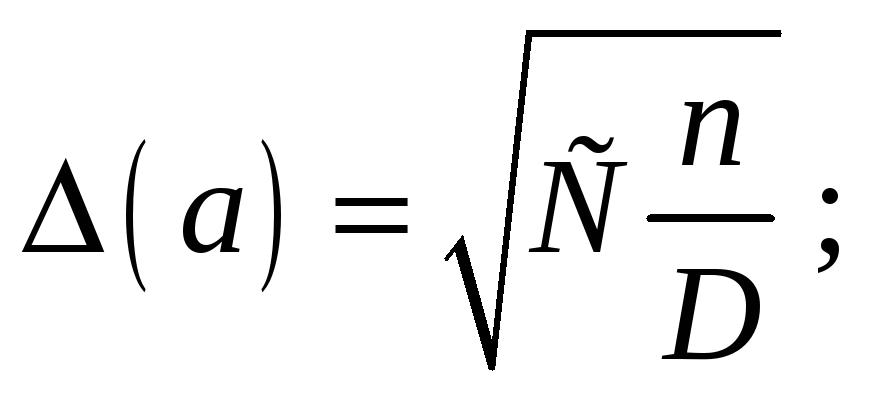
(3.8)

где

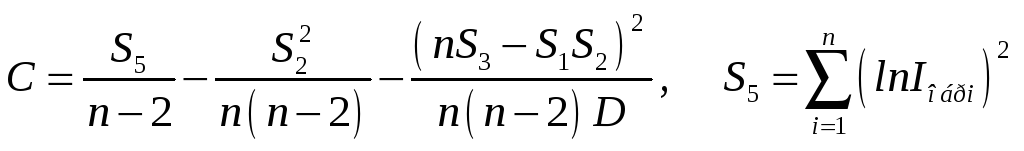
(3.9)

здесь величины n, S₁-S₄, D − те же, что в формулах 3.3-3.4

Относительная погрешность экспериментального определения ширины запрещенной зоны:

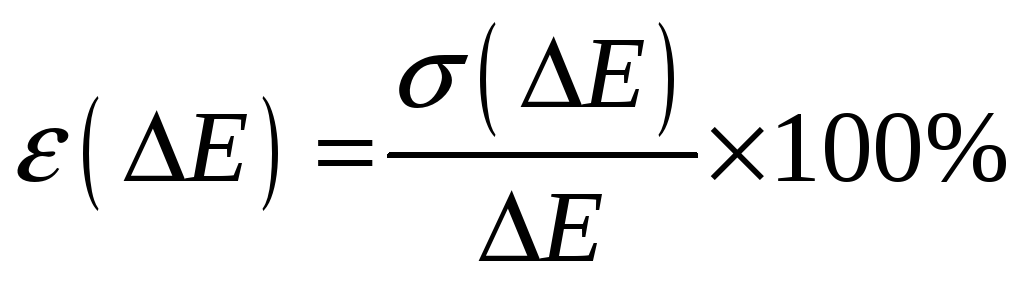
(3.10)

4. Результаты работы и их анализ.

Макет 19

Результаты экспериментальных измерений и их обработки представлены в таблице 4.1.

Результаты прямых и косвенных измерений. Таблица 4.1

№	Т, К	invT, 10-3 К-1	σ_invT, 10-3 К-1	Jret мкА	σ_Jret , мкА	ln_Jret	σ_ln Jret
1	308	3,247	0,005	0,0373	0,0001	-10,197	0,0027
2	318	3,145	0,005	0,0625	0,0001	-9,68	0,0016
3	328	3,049	0,005	0,102	0,001	-9,191	0,0098
4	338	2,959	0,004	0,160	0,001	-8,74	0,0063
5	348	2,874	0,004	0,246	0,001	-8,31	0,0041
6	358	2,793	0,004	0,370	0,001	-7,902	0,0027
7	368	2,717	0,004	0,542	0,001	-7,52	0,0018
8	378	2,646	0,003	0,78	0,01	-7,156	0,0013
9	388	2,577	0,003	1,10	0,01	-6,812	0,0091
10	398	2,513	0,003	1,53	0,01	-6,482	0,0065

Э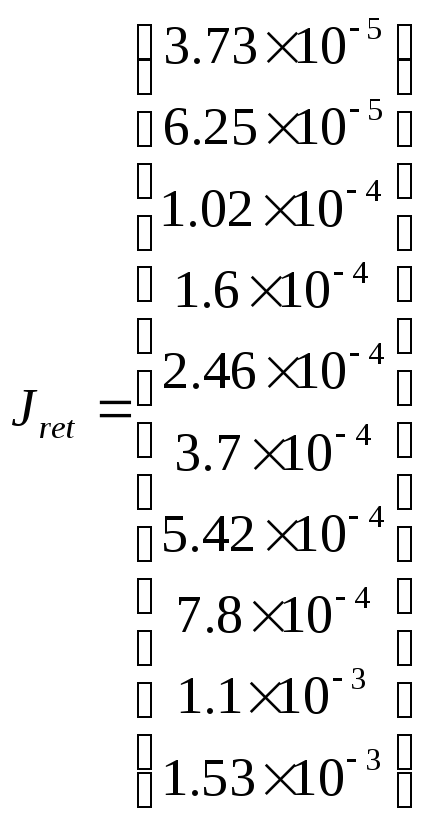кспериментальные данные, взятые из журнала измерений:

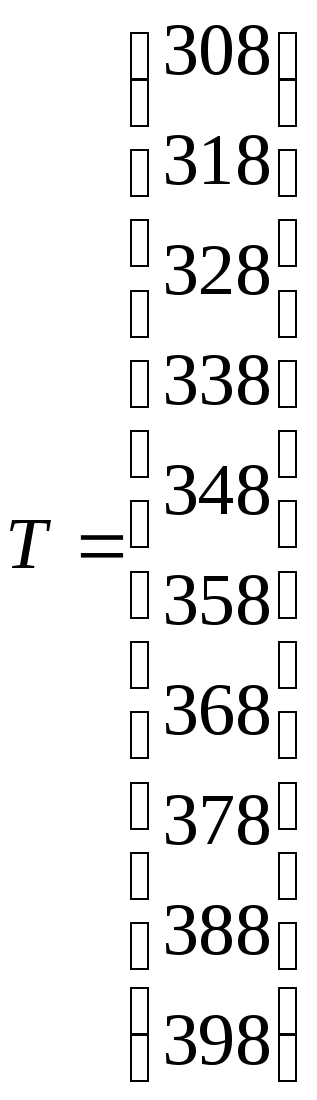
К , температуры внутри термостата

А, обратные токи диода

Вычислим значения, которые заносятся в итоговую таблицу:

Nd=10 количество измерений

i=1..Nd номера измерений

К^-1 , обратные значения температуры

Натуральные логарифмы обратных токов диода

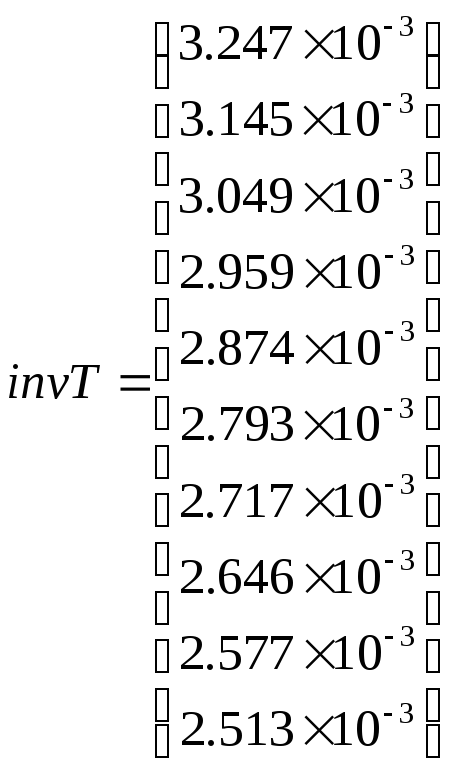
Абсолютная погрешность определения величины обратной температуры по формуле 3.6 с учетом значения 3.6a:

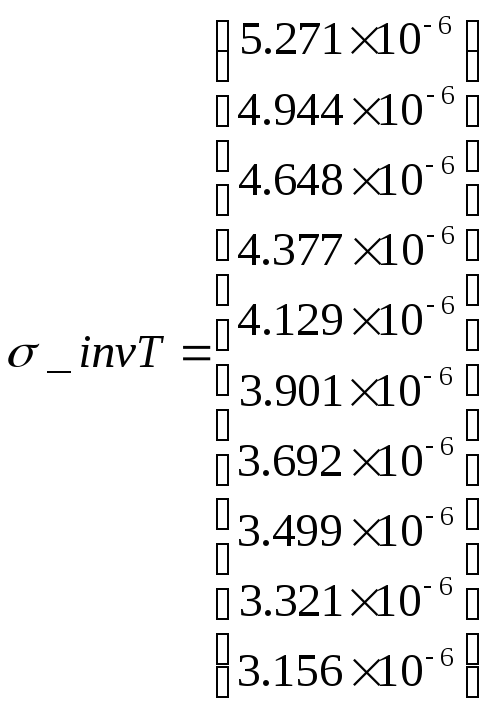
К^-1

А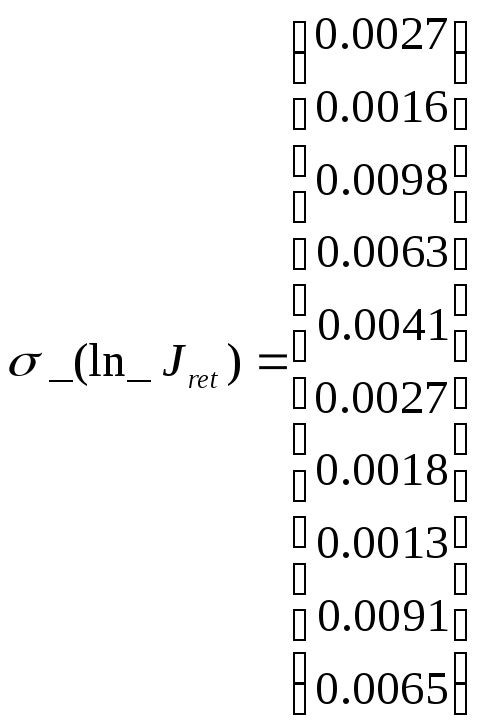бсолютная погрешность определения величины логарифма обратного тока по формуле 3.5 с учетом определения 3.5a:

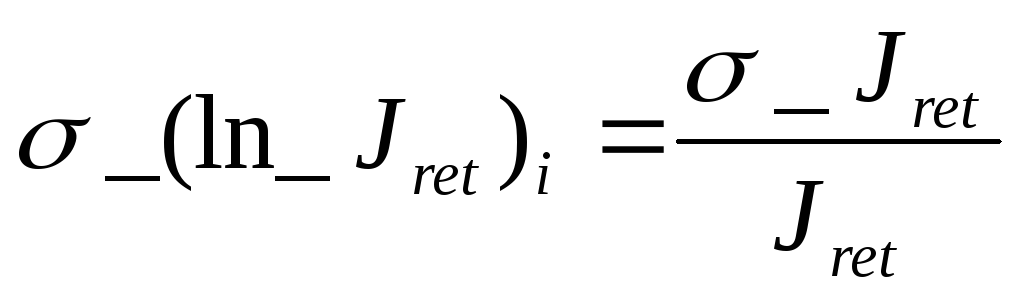
Для i=1,2 мкА

Для i=3-7 мкА

Для i=8-10 мкА

Построение графика.

Применим метод наименьших квадратов для построения прямой по экспериментальным точкам:

Угловой коэффициент прямой:

К

Отрезок, отсекаемый прямой от оси OY :

Абсолютные погрешности вычисления параметров прямой линии:

К

С учетом полученных параметров записываем уравнение прямой

ln(Jret)

1/Т, К^-1

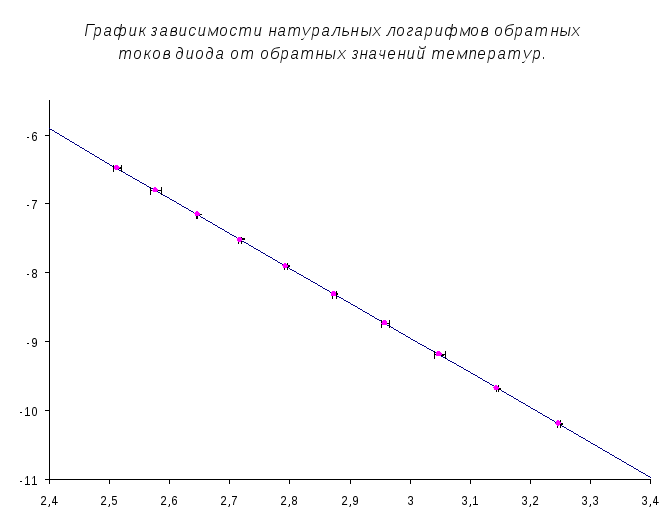
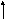
График зависимости натуральных логарифмов обратных токов диода от обратных значений температур. рис. 4.2

Постоянная Больцмана:

(электронвольтов на кельвин)

Вычислим ширину запрещенной зоны диода:

эВ

5. ВЫВОДЫ

В ходе лабораторной работы для определения ширины запрещенной зоны полупроводника была исследована температурная зависимость обратного тока стандартного диода, изготовленного из этого полупроводника – сняты показания значений температур внутри термостата и обратных токов диода. По экспериментальным точкам был построен график зависимости логарифма обратного тока диода ln_Jret от величины обратной температуры invT. Линейность график ln_Jret = f(invT) свидетельствует о выполнимости закона Jret = exp(-Е/(kT)) или в другой форме ln_Jret = lnJ_о - Е/(kT). Все точки в этой зависимости укладываются на прямую в пределах их погрешностей.

Рассчитано значение ширины запрещенной зоны полупроводника:

Е = 0.435 эВ

6. ОТВЕТЫ НА КОНТРОЛЬНЫЕ ВОПРОСЫ

1. Каков смысл понятий «валентная зона», «зона проводимости», «запрещенная зона»?

Зонная теория объясняет полупроводниковые свойства твердых тел на основе одноэлектронного приближения и распределения электронных энергетических уровней в виде разрешенных и запрещенных зон. Энергетические уровни электронов, участвующих в ковалентной связи, образуют верхнюю из заполненных разрешенных зон (валентную зону). Следующая по энергии разрешенная зона, уровни которой не заполнены электронами, − зона проводимости. Энергетический интервал между "дном" Е_c (минимумом энергии) зоны проводимости и "потолком" Е_v (максимумом) валентной зоны называется шириной запрещенной зоны ΔE.

В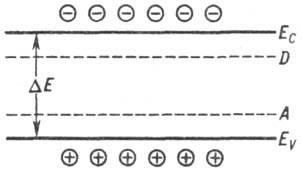алентная зона (кружки с плюсом дырки) и зона проводимости (кружки с минусом -электроны проводимости): E_с− дно зоны проводимости, E_V − потолок валентной зоны, ΔE− ширина запрещенной зоны, D и А − донорные и акцепторные уровни соответственно.

Рисунок 6.1.