Министерство образования РФ

Томский государственный университет

Систем управления и радиоэлектронике

(ТУСУР)

Центр дистанционного обучения.

Кафедра автоматизированных систем управления (АСУ)

Контрольная работа № 2

по дисциплине: «Технология разработки программного обеспечения»

тема: «Анализ нечисловой информации»

Вариант № 1

Автор методического пособия: Калайда В.Т. Романенко В.В.

Задание 1

1) Показать, что в четырехклеточной таблице

D = a - (a+c)(a+b)/n = (ad-bc)/n

2) Вычислить и проанализировать коэффициенты связи для

четырехклеточных таблиц

а)

9	1
1	9

б)

90	10
10	90

в)

900	100
100	900

Задание 2

Вычислить ранговые критерии

а) p1: 1 2 3 4 5 б) p1: 1 2 3 4.5 4.5 в) p1: 4 1 2 3 5

p2: 1 2 3 4 5 p2: 1.5 1.5 4 4 4 p2: 5 4 1 2 3

г) p1: 1 3 2 4 6 7 5

p2: 2 1 3 4 5 6 7

p3: 1 2 3 4 5 6 7

p4: 3 1 2 4 5 7 6

Задание 3

На основе данных исследования получена таблица

Возраст	Оценка состояния здоровья
	Не болею совсем	Болею редко	Болею часто	Совсем больной
До 25 лет	30	40	20	10
25-55 лет	10	20	60	10
Старше 55 лет	0	10	40	50

Есть ли и какова связь в оценке здоровья респондентов разных возрастов?

Указание: а) провести анализ при помощи ХИ-квадрат теста

б) вычислить [X/Y]

в) перейти к ранговым переменным и оценить согласованность мнений людей разных возрастов

Задание 1

1) Показать, что в четырехклеточной таблице

D = a - (a+c)(a+b)/n = (ad-bc)/n

2) Вычислить и проанализировать коэффициенты связи для четырехклеточных таблиц

а)

9	1
1	9

б)

90	10
10	90

в)

900	100
100	900

Решение:

1. Показать, что в четырехклеточной таблице

четырехклеточной таблице: , откуда

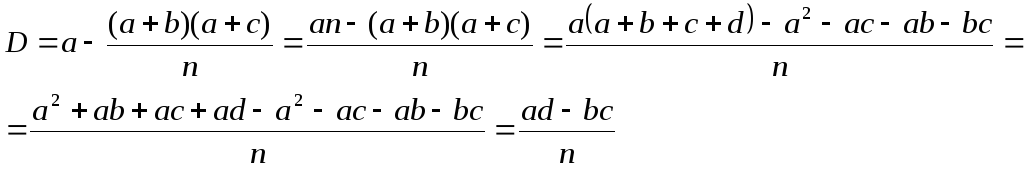
2. Вычислить и проанализировать коэффициенты связи для четырехклеточных таблиц

а)

9	1
1	9

Расчитаем коэффициент связи Юла:

Расчитаем коэффициент контингенции:

.

Критерий согласия:

Признаки очень сильно связаны.

б)

90	10
10	90

Расчитаем коэффициент связи Юла:

Расчитаем коэффициент контингенции:

.

Критерий согласия:

Признаки очень сильно связаны.

в)

900	100
100	900

Расчитаем коэффициент связи Юла:

Расчитаем коэффициент контингенции:

.

Критерий согласия:

Во всех трех таблицах признаки связаны сильно и различаются только критерии согласия.

Задание 2

Вычислить ранговые критерии

а) p1: 1 2 3 4 5 б) p1: 1 2 3 4.5 4.5 в) p1: 4 1 2 3 5

p2: 1 2 3 4 5 p2: 1.5 1.5 4 4 4 p2: 5 4 1 2 3

г) p1: 1 3 2 4 6 7 5

p2: 2 1 3 4 5 6 7

p3: 1 2 3 4 5 6 7

p4: 3 1 2 4 5 7 6

Решение:

Вычислить ранговые критерии

а) p1: 1 2 3 4 5

p2: 1 2 3 4 5

Находим ранговый коэффициент корреляции Спирмэна:

. Величина этого коэффициента равного единице, говорит о наличии сильной связи между ранжировками. Теперь находим ранговый коэффициент корреляции Кендалла:

. Величина этого коэффициента равного 1, так же говорит о наличии сильной связи между ранжировками.

б) p1: 1 2 3 4.5 4.5

p2: 1.5 1.5 4 4 4

Находим ранговый коэффициент корреляции Спирмэна по формулам, но здесь имеются группы неразличимых рангов:

; ;

Величина этого коэффициента, приближается к единице, это говорит о наличии связи между ранжировками. Теперь находим ранговый коэффициент корреляции Кендалла:

; ; ;

. Величина этого коэффициента, тоже говорит о наличии связи между ранжировками.

в) p1: 4 1 2 3 5

p2: 5 4 1 2 3

Находим ранговый коэффициент корреляции Спирмэна:

. Величина этого коэффициента, равного 0,2, говорит о наличии слабой связи между ранжировками. Теперь находим ранговый коэффициент корреляции Кендалла, для этого необходимо упорядочить любую из двух выборок.

p1: 1 2 3 4 5

p2: 4 1 2 5 3

. Величина этого коэффициента, равного 0,2, тоже говорит о наличии слабой связи между ранжировками.

г) p1: 1 3 2 4 6 7 5

p2: 2 1 3 4 5 6 7

p3: 1 2 3 4 5 6 7

p4: 3 1 2 4 5 7 6

Здесь ранжировок больше двух, то вычисляем коэффициент конкорданации:

Из этого результата видно, что при оценке объектов между экспертами присутствует сильная связь и согласие между ними.

Задание 3

На основе данных исследования получена таблица

Возраст	Оценка состояния здоровья
	Не болею совсем	Болею редко	Болею часто	Совсем больной
До 25 лет	30	40	20	10
25-55 лет	10	20	60	10
Старше 55 лет	0	10	40	50

Есть ли и какова связь в оценке здоровья респондентов разных возрастов?

Указание: а) провести анализ при помощи ХИ-квадрат теста

б) вычислить [X/Y]

в) перейти к ранговым переменным и оценить согласованность мнений людей разных возрастов

Решение:

а) выдвигаем гипотезу о том, что связи в оценке здоровья респондентов разных возрастов нет.

Вычислим где

30	40	20	10	100
10	20	60	10	100
0	10	40	50	100
40	70	120	70	300

Теперь нахожу значение , для этого определим число степеней свободы:

Тогда при находим по таблице

Если то гипотеза о том, что связь в оценке здоровья мужчин и женщин отсутствует, не подтверждается (связь имеется), иначе нет.

б) рассчитаем направленный (несимметричный):

Здесь и далее предполагается, что уровни (градации) признака - строки, - столбцы.

Ненаправленный (симметричный) коэффициент :

в) перейдем к ранговым коэффициентам:

				
4	3	2	1	10
1	2	4	1	9
1	2	3	4	10

Имеются объединенные ранги, поэтому рассчитываем коэффициент конкордации (согласия экспертов) по формуле:

где

Рассчитываем поправки:

и коэффициент:

Вычисляем статистику:.

Теперь необходимо найти по таблице теоретическое значение при и числе степеней свободы . Если , то гипотеза об отсутствии связи отвергается, т.е. согласованность признаков значима, иначе гипотеза об отсутствии связи подтверждается.