Министерство образования РФ

Томский государственный университет

Систем управления и радиоэлектронике

(ТУСУР)

Центр дистанционного обучения.

Кафедра автоматизированных систем управления (АСУ)

Контрольная работа № 1

по дисциплине: «Технология разработки программного обеспечения»

тема: «Анализ нечисловой информации»

Вариант № 1

Автор методического пособия: Калайда В.Т. Романенко В.В.

Задание 1

Даны четырехклеточные таблицы:

а) в социологическом исследовании опрошено 190 человек. Получена таблица:

100	0
0	100

б) в ходе исследования было обследовано 500 предприятий. Получена таблица:

100	100
100	100

в) в исследовании опрошено 150 человек. Получена таблица:

100	0
0	50

1) Есть ли связь между признаками в таблицах?

2) Какова сила связи между признаками в таблицах?

3) Получите формулы для вычисления отклонения фактической

частоты от "независимой" в таблице 2х2 для клеток a и b.

Сделайте вывод.

Задание 2

Вычислить ранговые критерии

а) p1: 3 2 1 4 б) p1: 1 2 3 4 в) p1: 5 2 3 4

p2: 3 2 1 4 p2: 3 1 4 2 p2: 4 3 2 1

г) p1: 2 2 2 4 5 д) p1: 1 2 3 е) p1: 1 2 3

p2: 1 4 2.5 2.5 5 p2: 1 2 3 p2: 3 2 1

p3: 1 2 3 p3: 2 2 2

p4: 1 2 3 p4: 2 2 2

Задание 3

На основе данных исследования получена таблица

Пол	Оценка состояния здоровья
	Не болею совсем	Болею редко	Болею часто	Совсем больной
Мужской	10	20	60	10
Женский	5	20	65	10

Есть ли и какова связь в оценке здоровья мужчин и женщин?

Указание: а) провести анализ при помощи ХИ-квадрат теста

б) вычислить [X/Y]

в) перейти к ранговым переменным и оценить

согласованность мнений

Задание 1

Даны четырехклеточные таблицы:

а) в социологическом исследовании опрошено 190 человек. Получена таблица:

100	0
0	100

б) в ходе исследования было обследовано 500 предприятий. Получена таблица:

100	100
100	100

в) в исследовании опрошено 150 человек. Получена таблица:

100	0
0	50

1) Есть ли связь между признаками в таблицах?

2) Какова сила связи между признаками в таблицах?

3) Получите формулы для вычисления отклонения фактической частоты от "независимой" в таблице 2х2 для клеток a и b.

Решение:

1) Есть ли связь между признаками в таблицах?

а) Наблюдательная частота 100 > 53, следовательно a и b положительно связаны.

б) Наблюдательная частота 100 > 80, следовательно a и b положительно связаны.

в) Наблюдательная частота 100 > 33, следовательно a и b положительно связаны.

2) Какова сила связи между признаками в таблицах?

Рассмотрим разность между наблюденной частотой и частотой, полученной в предположении, что признаки независимы, для клетки ():

Это коэффициент ассоциации Юла:

а) , полная связанность A и В.

б) , признаки A и В независимы.

в) , полная связанность A и В.

3) Получите формулы для вычисления отклонения фактической частоты от "независимой" в таблице 2х2 для клеток a и b.

Отсюда видно, что

Задание 2

Вычислить ранговые критерии

а) p1: 3 2 1 4 б) p1: 1 2 3 4 в) p1: 5 2 3 4

p2: 3 2 1 4 p2: 3 1 4 2 p2: 4 3 2 1

г) p1: 2 2 2 4 5 д) p1: 1 2 3 е) p1: 1 2 3

p2: 1 4 2.5 2.5 5 p2: 1 2 3 p2: 3 2 1

p3: 1 2 3 p3: 2 2 2

p4: 1 2 3 p4: 2 2 2

Решение:

а) p1: 3 2 1 4

p2: 3 2 1 4

Сначала находим коэффициент корреляции Спирмэна по формуле

. Величина этого коэффициента =1, это говорит о наличии сильной связи между ранжировками. Находим ранговый коэффициент корреляции Кэндалла по формуле, но сначала нужно упорядочить любую из двух выборок.

p1: 1 2 3 4 . Величина этого коэффициента, равного единице,

p2: 1 2 3 4 тоже говорит о наличии сильной связи между ранжировками.

б) p1: 1 2 3 4

p2: 3 1 4 2

Сначала находим коэффициент корреляции Спирмэна по формуле

. Величина этого коэффициента =0, это говорит о наличии слабой связи между ранжировками. Находим ранговый коэффициент корреляции Крэндалла по формуле

. Величина этого коэффициента, равного нулю, это тоже говорит о наличии слабой связи между ранжировками.

в) p1: 5 2 3 4

p2: 4 3 2 1

Сначала находим коэффициент корреляции Спирмэна по формуле

. Величина этого коэффициента =-0,2, это говорит о наличии слабой связи между ранжировками. Находим ранговый коэффициент корреляции Кэндалла по формуле, но сначала нужно упорядочить любую из двух выборок.

p1: 4 3 2 5 Ошибка: в первой ранжировке не может быть 5, т.к. у нас все 4 объекта

p2: 1 2 3 4

. Величина этого коэффициента, равного нулю, это тоже говорит о наличии слабой связи между ранжировками.

г) p1: 2 2 2 4 5

p2: 1 4 2.5 2.5 5

Находи ранговый коэффициент корреляции Спирмэна по формулам, так как имеются группы неразличимых рангов:

;

Величина этого коэффициента, =0,97, это говорит о наличии связи между ранжировками.

Находим ранговый коэффициент корреляции Кендэла по формулам:

; ; ;

Величина этого коэффициента, =0,76, это говорит о наличии связи между ранжировками.

д) p1: 1 2 3

p2: 1 2 3

p3: 1 2 3

p4: 1 2 3

Так как ранжировок больше двух, то вычисляем коэффициент конкорданации (согласия экспертов) по формуле:

Из полученного результата видно, что при оценке объектов между экспертами присутствует слабая связь и несогласие между ними.

е) p1: 1 2 3

p2: 3 2 1

p3: 2 2 2

p4: 2 2 2

Так как ранжировок больше двух, то вычисляем коэффициент конкорданации (согласия экспертов) по формуле:

Из полученного результата видно, что при оценке объектов между экспертами отсутствует связь и согласие между ними.

Задание 3

На основе данных исследования получена таблица

Пол	Оценка состояния здоровья
	Не болею совсем	Болею редко	Болею часто	Совсем больной
Мужской	10	20	60	10
Женский	5	20	65	10

Есть ли и какова связь в оценке здоровья мужчин и женщин?

Указание: а) провести анализ при помощи ХИ-квадрат теста

б) вычислить [X/Y]

в) перейти к ранговым переменным и оценить согласованность мнений

Решение:

а) Выдвигаем гипотезу о том, что связи в оценке здоровья мужчин и женщин нет.

Вычислим где

10	20	60	10	100
5	20	65	10	100
15	40	125	20	200

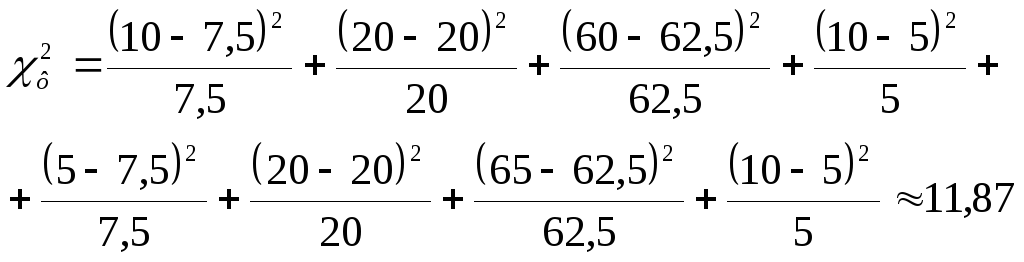
Теперь нахожу значение , для этого определим число степеней свободы:

Тогда при находим по таблице

Если то гипотеза о том, что связь в оценке здоровья мужчин и женщин отсутствует, не подтверждается (связь имеется), иначе нет.

б) Рассчитаем направленный (несимметричный):

Здесь и далее предполагается, что уровни (градации) признака - строки, - столбцы.

Ненаправленный (симметричный) коэффициент :

в) перейдем к ранговым коэффициентам:

1	2	3	1
1	3	4	2

Находим ранговый коэффициент корреляции Спирмэна по формулам общего случая:

Находим ранговый коэффициент корреляции Кэнделла по формулам общего случая:

Упорядочим вторую строку

1	1	2	3
1	2	3	4

Величины значений коэффициентов говорят о наличии сильной связи между ранжировками (т.е. согласованности мнений).