1.2.2 Абстрактнi автомати першого та другого роду

Абстрактнi автомати бувають першого та другого роду.

Закон функціонування абстрактного автомату першого роду задається наступними рівняннями:

Кажуть, що абстрактний автомат першого роду задається звичайною функцією виходів.

Закон функціонування абстрактного автомату другого роду задається наступними рівняннями:

Кажуть, що абстрактний автомат другого роду задається зсунутою функцією виходів.

1.2.3 Відображення, що породжуються абстрактними автоматами

Кожен абстрактний автомат породжує деяке відображення

,

яке реалізується в наведений нижче спосiб.

Кожне вхідне слово, тобто слово p=x_i1….x_ik у вхідному алфавіті Х ( , ) послідовно, лiтера за лiтерою, подається на вхід абстрактного автомату А, що завчасно був встановлений у початковий стан a0.

У результаті, виникає кінцева послідовність вхідних сигналів , яка, на основі закону функціонування абстрактного автомату, викликає появу однозначно визначної кінцевої послідовності вихідних сигналів. Зазначену послідовність називають вихідним словом g, що відповідає вхідному слову .

В силу довільності вибору слова , отримуємо деяке відображення , таке що .

Побудоване відображення називають відображенням, яке породжується абстрактним автоматом А.

1.2.4 Еквівалентні абстрактнi автомати, теорема про інтерпретацію абстрактного автомату другого роду як абстрактного автомату першого роду

Два абстрактних автомати зі спільними вхідним і вихідним алфавітами називають еквівалентними, якщо вони породжують однакове відображення.

Теорема 1. Для будь-якого абстрактного автомату другого роду існує еквівалентний абстрактний автомат першого роду , функцiю виходiв якого отримано в результаті підстановки функції переходів абстрактного автомату А до його зсунутої функцiї виходiв.

Дійсно, якщо задано довільний абстрактний автомат А другого роду, то, з закону функціонування абстрактних автоматiв другого роду, отримуємо наступну рiвнiсть: .

Із даної рівності випливає, що абстрактний автомат В першого роду, заданий тією ж функцiєю переходiв (а,х), що й автомат А, та функцiєю виходiв (за умови збереження множини станів, початкового стану, вхідного та вихідного алфавітів абстрактного автомату А), породжує те саме відображення множини вхідних слів у множину вихідних слів, що й абстрактний автомат А.

Наведений вище спосіб зведення абстрактних автоматiв другого роду до абстрактних автоматiв першого роду називають інтерпретацією абстрактного автомату другого роду як абстрактного автомату першого роду.

Зворотна інтерпретація абстрактного автомату першого роду як абстрактного автомату другого роду, при збереженні тієї самої множини станів, виявляється, взагалі кажучи, неможливою.

1.2.5 Автомати Мiлi та Мура, скінченні та нескінченні абстрактнi автомати

Автоматами Мілі (А Мілі) називають довільні абстрактнi автомати першого роду.

Автоматами Мура (А Мура) називають частковий випадок абстрактних автоматiв другого роду, для яких зсунута функція виходів не залежить від вхідного сигналу , тобто .

Абстрактнi автомати називають скiнченними (або нескінченними) залежно від того, чи є скінченною (або нескінченною) множина їх станів.

Виходячи із міркувань практики, об’єктом подальшого вивчення будуть скінченні автомати Мілі та Мура.

1.3 Способи задавання абстрактних автоматiв Мілі та Мура

1.3.1 Табличний спосіб задавання абстрактних автоматiв Мілі та Мура

Оскільки скінченні множини можуть бути задані перерахуванням їх елементів, то проблема задавання скінченних абстрактних автоматiв зводиться до проблеми задавання їх функцій переходiв і виходiв.

Функції переходiв і виходiв задаються таблицями переходів (ТП) і таблицями виходів (ТВ) або за допомогою графів переходів і виходів.

Задавання абстрактних автоматiв за допомогою таблиць переходiв i виходiв передбачає наступне:

- рядки таблиць позначаються вхідними сигналами абстрактного автомату, а стовпчики – його станами;

- початковий стан позначають у першому ліворуч стовпчику;

- на перетині х-го рядка та а-го стовпчика в таблицi переходiв проставляють значення (а,х), а в таблицi виходiв (звичайній або зсунутій) – значення (а,х).

Задавання таблиць переходiв i виходiв у вказаному вигляді повністю визначає кінцевий абстрактний автомат (задаються не тільки функції переходiв i виходiв, а й множини вхідних і вихідних станів, початковий стан).

Для автомату Мура, зсунута функцiя виходiв зводиться до одного рядка.

Якщо розмістити вказаний рядок над таблицею переходiв, то отримаємо позначену (відмічену) таблицю переходiв абстрактного автомату Мура.

У позначенiй таблицi переходiв, над кожним станом а_і, що позначає певний стовпчик таблицi переходiв, ставиться відповідний даному стану вихідний сигнал λ(а_і).

Кажуть, що в довільному абстрактному автоматi Мура кожен стан аі позначений відповідним йому вихідним сигналом λ(а_i).

1.3.2 Графовий спосіб задавання абстрактних автоматiв Мілі та Мура

Другий спосіб задавання абстрактних автоматiв базується на використанні направлених графів.

Граф абстрактного автомату А є комбінацією наступних об`єктiв:

- вершин графу, що ототожнюються зі станами абстрактного автомату (зображуються на рисунках за допомогою кiл);

- ребер графу, що ототожнюються з вхідними сигналами абстрактного автомату (зображуються на рисунках за допомогою стрілок, що з’єднують вершини).

Якщо вхідний сигнал х викликає перехід абстрактного автомату зі стану а_і до стан а_к, то на графі даному переходу відповідає рисунок наступного виду:

Рисунок 1

Також не включається випадок, коли вершини аі та ак співпадають:

Рисунок 2

Побудований у вказаний вище спосiб граф абстрактного автомату А задає лише функцiю переходiв даного автомату.

Для задавання функції виходiв абстрактного автомату, ребра графу позначаються не тільки вхідними, але і відповідними вихідними сигналами.

Якщо позначена вхідним сигналом х стрілка з’єднує вершини а_і та а_к, то їй приписується наступний вихідний сигнал:

- у випадку абстрактного автомату першого роду - λ1(а_і,х), де λ1 є звичайною функцiєю виходiв абстрактного автомату;

- у випадку абстрактного автомату другого роду - λ2(а_к,х), де λ2 є зсунутою функцiєю виходiв абстрактного автомату.

У випадку автомату Мура, всі стрілки, що входять в одну і ту ж вершину ак, повинні бути позначені одним і тим же вихідним сигналом, а тому прийнято позначати вихідним сигналом не стрілки, а вершини, в які дані стрілки входять.

Граф абстрактного автомату, завдяки введеним на ньому позначенням на вершинах та ребрах, повністю задає абстрактний автомат.

Перехід від задавання абстрактного автомату за допомогою таблиць, до його задавання за допомогою графів виконується в наведений нижче спосiб.

Нехай автомат Мура задано позначеною таблицею переходів 1.

Таблиця 1

	U	U	V	V
	1	2	3	4
X	2	3	3	2
Y	1	4	4	1

Даній таблицi переходiв відповідає граф, представлений на рисунку 3.

Рисунок 3

1.3.3 Інтерпретація абстрактного автомату Мура, заданого таблично або графово, як абстрактного автомату Мілі

При обох способах задавання абстрактного автомату, особливо просто здійснюється інтерпретація довільного автомату Мура А, як автомату Мiлi В:

- у випадку задавання А позначеною таблицею переходiв, для отримання еквівалентного автомату В, необхідно у позначенiй таблицi переходiв автомату Мура замість станів підставити вихідні сигнали, що позначають їх;

- у випадку задавання А графом, для отримання з А В, досить позначити вихідними сигналами не вершини, а стрілки, що входять у відповідні вершини.

Якщо застосувати дану процедуру до автомату Мура, поданого графом на рисунку 3, то отримаємо еквівалентний автомат Мілі, заданий наведеними нижче: таблицями переходiв (лiворуч) i виходiв (праворуч); графом.

Таблиця 2 Таблиця 3

	1	2	3	4
X	2	3	3	2
Y	1	4	4	1

	1	2	3	4
X	u	Υ	Υ	U
Y	u	Υ	Υ	U

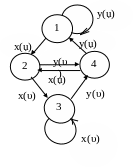Рисунок 4