
11- 4_Теория вероятностей
.doc
Министерство общего и профессионального образования
Российской Федерации
ТОМСКИЙ ГОСУДАРСТВЕННЫЙ УНЕВЕРСИТЕТ СИСТЕМ
УПРАВЛЕНИЯ И РАДИОЭЛЕКТРОНИКИ (ТУСУР)
Теория Вероятности
Преподаватель:
Контрольная работа №11
(в-4)
Студент гр.
Проверил преподаватель:
ТОМСК-2
-
В коробке 4 одинаковых занумерованных кубика. По одному извлекают все кубики. Найти вероятность того, что номера извлечённых кубиков появляются в возрастающем порядке.
Вероятность
вытащить кубик с номером 1 равна
![]() (
так как кубиков 4).
(
так как кубиков 4).
![]() вытаскивается
кубик с номером 1
вытаскивается
кубик с номером 1
![]() вытаскивается
кубик с номером 2
вытаскивается
кубик с номером 2
![]() вытаскивается
кубик с номеров 3
вытаскивается
кубик с номеров 3
![]() вытаскивается
кубик с номером 4
вытаскивается
кубик с номером 4
Вероятность
вытащить кубик с номером 2 равна
![]()
Вероятность
вытащить кубик с номеров 3 из оставшихся
равна
![]()
Вероятность
вытащить кубик с номером 4 из оставшихся
равна
![]()
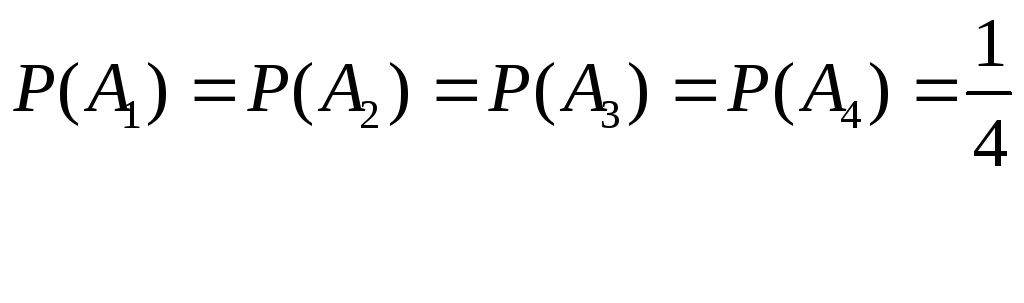
![]()
![]()
Ответ:
![]()
2.Выстрелив один раз, стрелок уступает очередь другому. У каждого стрелка Вероятность попадания каждым из них при одном выстреле равно 0.2. Приз получает стрелок , первым попавшим в цель. Найти вероятность того. Что приз получит стрелок, попавший стрелять первым.
![]() первый
стрелок попадает с 1 выстрела.
первый
стрелок попадает с 1 выстрела.
![]() второй
стрелок попадает с первого выстрела.
второй
стрелок попадает с первого выстрела.
![]() первый
стрелок попадает со 2 выстрела.
первый
стрелок попадает со 2 выстрела.
![]() первый
игрок получает приз.
первый
игрок получает приз.
Очевидно,
что
![]()
Все события независимы, поэтому вероятность события C равна:
![]() Ответ:
P(C)=0,84.
Ответ:
P(C)=0,84.
3.Вероятность попадания в цель при одном выстреле равна 0,05 и не меняется от выстрела к выстрелу. Сколько нужно сделать выстрелов, чтобы с вероятностью 0.75 иметь хотя бы одно попадания. Все события ( выстрелы по мишени) являются несовместными, поэтому количество выстрелов можно определить следующим образом:
Все события являются несовместными. Пусть n- количество выстрелов равна 0,75. Следовательно, вероятность того. Что все выстрелы будут мимо цели равна 1-0,75=0,25
То
есть,
![]()
Где
![]() -Стрелок
поражает цель в n-
ой попытке .По условию
-Стрелок
поражает цель в n-
ой попытке .По условию
![]() следовательно,
следовательно,
![]()

следовательно.![]()
Ответ:![]()
4.Имеются две партии изделий, состоящих из 10 изделий каждая, по 6- первого сорта и 4- второго. Из первой партии извлекли изделия и переложили во вторую, после чего из второй партии берут одно изделие. Найти вероятность того, что оно второго сорта.
1) А-изделие 2 сорта из 2 партии
![]() изделие
2 сорта из 1 партии.
изделие
2 сорта из 1 партии.
Следовательно,
![]()
П осле
переложения изделия из 1 партии во вторую
в ней останется 11- изделий: 6-первого
сорта, 5- второго сорта. Следовательно,
условная вероятность
![]()
Следовательно, по формуле:
![]()
Ответ:![]()
2)
![]() изделие
1 сорта из 1 партии
изделие
1 сорта из 1 партии
Следовательно.
![]()
После данного события во второй партии будет 7 изделий 1 сорта и 4 изделия 2 сорта.
Условная вероятность равна:
![]()
Следовательно
![]()
Теперь найдём полную вероятность
![]()
Ответ: 0.4
5.
Вероятность того, что деталь первого
сорта, равна 0,2. Отобрано 4 детали х- число
деталей первого сорта среди отобранных.
Найти: а) ряд распределения х; б) функцию
распределения F(
x):
в)![]() ;
г)
;
г)
![]() ;
;
д)
![]()
а) Случайная вероятность Х имеет область значений {0,1,2,3,4}.Случайная величина распределена по схеме Бернулли, поэтому вероятности значений Х можно найти по формуле:
![]()
![]()
![]()
 Следовательно,
ряд распределения Х имеет следующий
вид:
Следовательно,
ряд распределения Х имеет следующий
вид:
|
Х 0 1 2 3 4
|
|
p 0,4096 0, 4096 0,1536 0,0256 0,0016
|
б)Перейдём от ряда распределения к функции распределения:

в)
Найдём математическое ожидание
![]()
![]()
г)
Найдём дисперсию случайной величины
![]()

6. Дана плотность распределения вероятностей
![]() случайной
величины Х.
случайной
величины Х.
Найти
а) константу a;
б) функцию распределения F(x):
в)![]() ;
г)
;
г)
![]()
д)
![]()
а) Найти константу а. Применим условия нормировки.
![]() Вычислим
интеграл.
Вычислим
интеграл.
 Следовательно,
а=1.
Следовательно,
а=1.
б) Если. х<0, то функция распределения будет иметь вид:
![]()
Следовательно, функция распределения равна:

в)
![]() Найдём
математическое ожидание, используя
формулу.
Найдём
математическое ожидание, используя
формулу.

г)
Найдём дисперсию случайной величины
![]()

д)

7. Систематическая ошибка высотомера отсутствует, а случайные ошибки распределены по нормальному закону. Какую среднеквадратическую ошибку должен иметь высотомер, чтобы с вероятностью 0,9 ошибка измерения высоты по модулю была меньше 100м. Для решения воспользуемся интегральной теоремой Муавра-Лапласа:
![]() где
Ф-функция Лапласа.
где
Ф-функция Лапласа.

Найдём аргумент функции Лапласа по таблице. Получим:

