2- 8_ТВМС

Томский межвузовский центр дистанционного образования

Томский государственный университет

систем управления и радиоэлектроники (ТУСУР)

Контрольная работа №2

Вариант № 8

по дисциплине «ТВМС и СП»

(Учебное пособие «Теория вероятностей» автор Магазинников Л. И.,2000г.)

г. Норильск

2007 г

1. Дана матрица распределения вероятностей системы (X,Y)

	X
Y		-1	0	3
2		0.1100	0.2500	0.1400
3		0.1200	0.2000	0.1800

Найти: а) ряды распределений X и Y; б) ; в) ; г) ; д) ; е) ; ж) , округлить до 0,01; з) ряд распределения Y, если X = 0; и) , округлить до 0.01

Решение.

а) ряд распределений X:

X	-1	0	3
Р	0,2300	0,4500	0,3200

ряд распределений Y:

Y	2	3
P	0,500	0,500

б)

в)

г)

	2,9929	0,5329	5,1529
Р	0,23	0,45	0,32

д)

	0,25	0,25
P	0,5	0,5

е)

ж)

з) находим ряд распределения Y, если X = 0 используя формулу

P(Y = 2/X = 0) = 0.25/0.45 = 5/9

P(Y = 3/X = 0) = 0.2/0.45 = 4/9

Получаем:

Y	2	3
P(Y/X = 0)	5/9	4/9

и) .

2. Дана плотность распределения вероятностей системы (X,Y)

Найти: а) константу С; б) ; в) ; г) ; д) ) ; е) ; ж) ; з) ; и) F(2,1); к) .

Решение.

а)

б) Найдем плотности компонент X,Y

в) Найдем математическое ожидание

г) Найдем математическое ожидание

д) Находим дисперсию

е) Находим дисперсию

ж) Найдем ковариацию случайных величин X,Y

з) Найдем коэффициент корреляции случайных величин X,Y

и) Находим функцию распределения

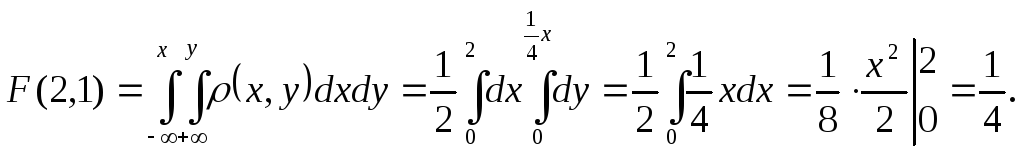
к) Найдем условные математические ожидания

, где

;

Эта условная плотность отлична от нуля только при , т.к. вдоль прямой y = ½ плотность . Таким образом,

3. По данным выборки объема n = 12 нормально распределенной случайной величины X найдена исправленная дисперсия . Найти доверительный интервал, содержащий среднее квадратичное отклонение величины X с вероятностью 0,99. В ответ ввести координату правого конца интервала.

Решение.

Задача сводится к отысканию величины q. По таблицам для значений q находим, что при n=12, величина q = 0.90. Т.к. q<1, то доверительный интервал ищем в виде

Получаем

5