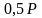2.1. Кинематический анализ заданной расчетной схемы фермы.

Обозначим цифрами узлы фермы.

Рис. 2. Нумерация узлов фермы

Определяем число степеней свободы:

,

где У – число узлов фермы (У=10);

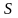- число стержней фермы ( =17; 4 стержня верхнего пояса; 4 стержня нижнего пояса; 5 стоек; 4 стержня-раскоса);

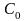- число опорных стержней ( =3; один в опоре В и два в опоре А).

Откуда получаем:

.

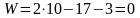Таким образом, заданная расчетная схема фермы обладает свойством статической определимости.

Проверку свойства мгновенной неизменяемости проведем на основе анализа структуры решетки заданной расчетной схемы. Мгновенная неизменяемость обеспечивается шарнирно-стержневыми треугольниками.

Для определения внутренних усилий необходимо сначала вычислить опорные реакции.

2.2. Определение опорных реакций.

Для определения реакций в опорах составим три уравнения равновесия для всей фермы в целом:

;

.

;

.

.

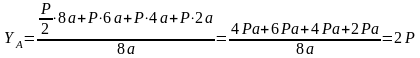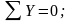
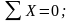
Рис. 3. К определению опорных реакций

2.3. Определяем усилия в стержнях фермы.

Первоначально будем считать все стержни растянутыми (усилие направлено от узла).

Рассмотрим равновесие узла 1 (рис. 4).

Рис. 4. Узел 1

Составляем уравнения равновесия:

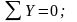
; (стержень сжат).

.

Рассмотрим равновесие узла 2 (рис. 5).

Ранее получили: .

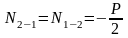Рис. 5. Узел 2

Составляем уравнения равновесия:

;

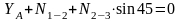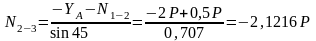(стержень сжат).

;

(стержень растянут).

Рассмотрим равновесие узла 3 (рис. 6).

Ранее получили: ;

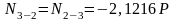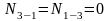
Рис. 6. Узел 3

;

.

;

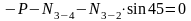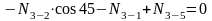(стержень сжат).

Рассмотрим равновесие узла 4 (рис.7).

Ранее получили: ; .

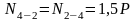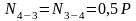Рис. 7. Узел 4

;

(стержень сжат).

;

(стержень растянут).

Рассмотрим равновесие узла 6 (рис. 8).

Ранее получили: .

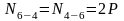Рис. 8. Узел 6

.

;

.

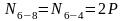Ферма симметрична, следовательно все усилия определены.

Рассмотрим равновесие узла 5 (рис. 9).

Так как все усилия определены, то проверим равновесие этого узла по вычисленным усилиям.

Рис. 9. Узел 5

;

;

;

.

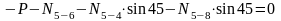Для проверки правильности определения усилий, рассмотрим также равновесие левой части фермы, отсеченной сквозным сечением (рис. 10).

Рис. 10. К рассмотрению равновесия части фермы,

отсеченной сквозным сечением.

;

.

;

.

;

.

;

;

;

.

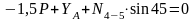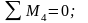
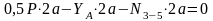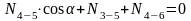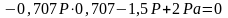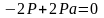Усилия в стержнях фермы определены верно.

Определение нагрузок на ферму.

На стропильную ферму покрытия могут действовать следующие нагрузки:

1. Постоянные – от веса ограждающих (кровля) и несущих (фермы, связи, прогоны) конструкций.

2. Кратковременные – атмосферные (снеговые, ветровые), технологические (от подвесного подъемно-транспортного оборудования, подвесных коммуникаций, электроосветительных установок, вентиляторов, галерей) и др.

Грузовая площадь для определения нагрузок на узел фермы составляет

.

Нагрузка на каждый узел фермы составляет:

.

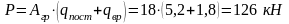Рис. 11. Схема расположения ферм.

1 – фермы; 2 – прогоны;

3 – грузовая площадь для определения нагрузок на ферму.

Вычисляем усилия в стержнях фермы с учетом полученного значения нагрузки .

Сводим результаты расчетов в таблицу 1.

Таблица 1

Усилия и геометрические длины стержней

Элемент		N, в долях Р	N, кН	Длина, в долях а	Длина, м
Верхний пояс	1-3 (7-9)	0	0	2а	3,0
	3-5 (5-7)		-189	2а	3,0
Нижний пояс	2-4 (8-10)		189	2а	3,0
	4-6 (6-8)		252	2а	3,0
Стойки	1-2 (9-10)	-0,5Р	-63	2а	3,0
	3-4 (7-8)		63	2а	3,0
	5-6	0	0	2а	3,0
Раскосы	2-3 (7-10)		-267,322	2,838а	4,243
	4-5 (5-8)		-89,082	2,838а	4,243

По максимальному усилию принимаем, согласно приложению 1, толщину фасонки равной 10 мм.