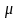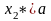1.5. Обмежений ріст при ненульовому початковому ефекті.

Визначимо нижню границю ефекту 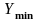, до якій прагне система при наближенні вхідних ресурсів до мінус безперервності. Рівняння росту

перетворимо ,

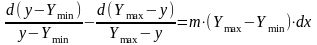про інтегруємо

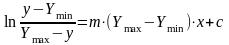
та знов перетворимо .

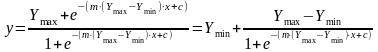2. Чисельне розв’язання диференціальних рівнянь

В звичайному диференціальному рівнянні

замінимо диференціали (нескінченні прирощення) на скінченні, але дуже малі

Перетворимо

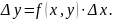
Оберемо крок інтегрування

Задамо початкові умови (точку з якої розпочнеться процес розвитку).

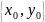
Розрахуємо значення правої частини диференціального рівняння в початкової точці

Знайдемо прирощення змінної розвитку

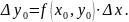
Знайдемо наступну точку розвитку.

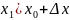
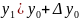
Повторимо процедуру для кожної наступної точки розвитку

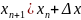
Більш складним є розв’язання рівнянь, в яких права частина містить змінні управління

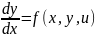
Такі рівняння в більшості випадків не піддаються аналітичному розв’язанню. І єдиним надійним способом залишається чисельне розв’язання, яке виконується аналогічно

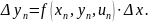
Завдання 1.

Розвиток технології NGN відбувається за логістичним законом.

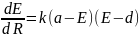
– коефіцієнт зростання;

– нижня асимптота (рівень, з якого стартує технологія);

– верхня асимптота (рівень, до якого спрямовується технологія).

Але за умовами розвитку ринку ця величина змінюється на кожному кроці розвитку.

Зростає внаслідок вдосконалення технологій.

Зменшується внаслідок обмежень юридичного характеру, пов’язаних з захистом навколишнього середовища;

Побудувати криву розвитку для початкових умов

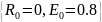
Крок інтегрування 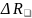задає викладач.

Півторить розрахунки ще для двох значень .

Оцініть різницю

3. Детермінований хаос.

Найпростіший способ підвищення точності чисельного розв’язання динамічних рівнянь (зменшення кроку інтегрування, періоду дискретизації) веде до збільшення витрат обчислювальних ресурсів. Похибки моделювання при збільшенні глибини прогнозування можуть досягати суттєвих величин. При певному співвідношенні параметрів дискретних логістичних рівнянь це може призвести до непередбаченої втрати якісної адекватності моделі у вигляді, так званого, детермінованого хаосу [286].

Зміна якісної картини чисельного розв’язання дискретних рівнянь впроаналізована в табл. та на рис. 3.44- 3.53.

Рис.		Поведінка рішення в околиці точки
Рис. 3.44	0.005	Якісна адекватність. Чисельні похибки.
Рис. 3.45	0.01	- // -
Рис. 3.46	0.033	Початок порушень адекватності. Похибка припустима.
Рис. 3.47	0.043	- // -
Рис. 3.48	0.06	- // -
Рис. 3.49	0.067	Коливальний процес. Похибка неприпустима.
Рис. 3.50	0.075	Хаос. Похибка неприпустима.
Рис. 3.51	0.09	- // -
Рис. 3.52	1.0	- // -
Рис. 3.53	1.0001	Зрив

Спочатку чисельне рішення якісно подібне аналітичному (точному), має у порівняні з ним деяку помилку, але впевнено сходиться до стійкої точки рівноваги (рис. 3.44- 3.46).

Рис. 3.44. =0.005 Рис. 3.45. =0.01 Рис. 3.46. =0.03

Потім якість рішення помітно погіршується: збільшується амплітуда коливань, середня, середня квадратична та максимальні значення помилок. (рис. 3.47, 3.48).

Рис. 3.47. =0.043 Рис. 3.48. =0.06 Рис. 3.49. =0.067

Далі спостерігається хаотична поведінка (рис. 3.50- 3.52). Як бачимо, зміна всього в 1.7 рази (рис. 3.47, 3.49) веде до хаосу, що підвищує вимоги до вибору періодів дискретизації логістичного рівняння.

Рис. 3.50. =0.075 Рис. 3.51. =0.09 Рис. 3.52. =0.1

Для реальних задач, в яких змінні мають конкретний фізичний сенс, можливим є „зрив” значень рішення у фізично неможливу від’ємну галузь (рис. 3.53).

Рис. 3.53. =0.10001