3. Оптимізаційне моделювання
Об’єкти стратегічного планування поділімо на програми розвитку та організаційні структури (разом з їх технічними та іншими матеріальними засобами). Об’єкти мають багато загального і за необхідністю можуть бути зведені в єдину структуру програм розвитку, наприклад, шляхом включення діяльності організаційних структур в програми фінансування.
Модель об’єкту має дозволяти прогнозувати розвиток подій, знаходити оптимальне рішення та прогнозувати наслідки його впровадження. Модель створюється відповідно до певних припущень та має відбивати найбільш суттєве в тій ситуації, в якій знаходиться об’єкт, в умовах прийнятої постановки задачі. Одному і тому ж об’єкту у різних умовах та на різних етапах життєвого циклу можуть відповідати різні моделі.
Складність моделі має відповідати складності процесу, а з другого боку - можливості щодо забезпечення вхідними даними. Чим складніша модель, тим складніше забезпечити її вхідними даними, тим вищий ступінь невизначеності, в якій вона функціонує. Отже, в більшості випадків модель повинна бути грубою.
Розглянемо адекватність грубих моделей на прикладі лінеаризованої моделі нелінійного процесу (рис.1.3).
Рис.1.3. Адекватність лінеарізованої моделі
A – початкова точка прогнозу. Інформація достовірна на 100%.
B – різниця між грубою і точною моделлю практично відсутня, тобто для практики несуттєва.
C – різниця суттєва, не дозволяє оцінити процес кількісно, але дозволяє оцінити якісно (в даному випадку - зробити висновок про те, що величина, що моделюється – зростає).
D – втрачена не тільки кількісна, але й якісна адекватність. Точне рішення показує, що реальний процес йде на спад, а груба лінійна модель, що зростає.
Як бачимо, адекватність моделі втрачається по мірі відходу від точки лінеаризації (А). Тому межі можливості застосування лінеарізованих та інших грубих моделей повинні визначатись чітко. Вдалим обранням грубої моделі можна досягти якісної адекватності у всьому діапазоні аргументів. Наприклад, не зважаючи на повну відмінність грубої моделі 2 від реального процесу, вона забезпечує довгостроковий прогноз кращій ніж груба модель 1.
В довгостроковому прогнозі чисельна точність – не головне. Точність - для бухгалтерії. Прийняттю рішень необхідна якісна адекватність. Для цього необхідно вилучити випадкові та другорядні складові та враховувати основні фактори процесу. Мистецтво виділити головне (основну тенденцію) є основою побудови моделі, яка адекватна постановці задачі й, отже, є визначним фактором прийняття правильних рішень.
Крім того, замовниками та головними експертами результатів моделювання є представники прикладної області, які не мають необхідної кваліфікації щодо моделювання. Рівень складності моделей має дозволяти їм розуміти та оцінювати адекватність не лише кінцевого, але й найбільш важливих проміжних результатів моделювання.
Цільовий ефект
Під оцінкою ефекту діяльності розуміємо встановлення ступеня відповідності стану організації до виконання завдань за призначенням згідно нормативів. Корисні ефекти вимірюватимемо у долях від нормативно повного виконання функцій. Аналогічно вимірюємо рівень забезпечення ресурсами. Вважаємо, що величина ресурсу або корисний ефект дорівнюють одиниці, якщо вони відповідають нормативам. Джерелами інформації виступають результати перевірок та інші звітні матеріали. Для узагальнення та зведення до співрозмірних величин показників оцінки готовності використовують згортки (мультиплікативні, адитивні тощо).
Для
створення ефекту
використовують вхідні
ресурси.
Під ресурсами
={
,
,
,
,
,
,
}
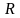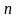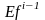розуміємо гроші
,
персонал
,
технічне забезпечення
,
матеріальні засоби
,
підрозділи
,
ефекти діяльності підпорядкованих
елементів структур
,
час
тощо. В залежності від постановки задачі
ресурси
,
,
,
,
можуть виступати у ролі фазових координат
або управлінь
.
Фазові координати – змінні у часі величини, які описують стан динамічного об’єкту (зазвичай такого, що описується диференціальними рівняннями). Інколи до фазових координат додають їх похідні.
Параметри – величини або функціональні залежності величин, які визначають найбільш суттєві властивості об’єкту. В стаціонарних системах параметри незмінні у часі. В нестаціонарних можуть мінятись.
Управління – змінні, які викликають зміну фазових координат у часі. Управління може мати конкретне технічне втілення (кут відхилення руля висоти) або бути просто фізично зрозумілим (перевантаження літака). Може бути взагалі абстрактним агрегуванням змінних, але у будь якому випадку управління використовується для свідомого впливу на фазові координати.
В цих термінах стратегічне планування передбачає послідовне виконання таких дій.
Створення системи: 1. Структурний синтез.
2. Параметричний синтез.
Управління системою: 3. Пошук управлінь.
Стан об’єктів змінюється в залежності від динаміки вхідних ресурсів та динамічних властивостей самих об’єктів. Якщо стан об’єкту змінюється повільно, то ним можна знехтувати. Формалізація моделей складних систем стратегічного планування завжди виконується з певними припущеннями.
Рішення оптимізаційних задач надають додаткову інформацію про об’єкти, що дозволяє спростити моделі та підвищити їх адекватність. Основні методологічні проблеми оптимізації в стратегічному плануванні викликані обмеженістю вхідних ресурсів, вимогами оперативності прийняття рішень, багатокритеріальністю, можливістю зміни цілей, пріоритетів та характеристик об’єктів на наступних етапах планування.
Складну систему слід декомпозувати на прості складові, побудувати моделі складових елементів, класифікувати відібрані моделі та оцінити можливість їх спрощення без втрати адекватності.
Оптимізаційна процедура має дозволити знайти рішення найкраще щодо цільового ефекту з урахуванням обмежень на фазові координати та управління. Для розв’язання оптимізаційної задачі необхідне виконання таких дій [3, 41, 210, 218, 243, 266]:
визначення мети операції;
визначення критерію ефективності (цільової функції) та обмежень;
визначення і при необхідності прогнозування вхідної інформації;
змістовна i формальна (математична) постановка задачі;
вибір (розробка) математичного апарату для розв'язання задачі;
аналіз результатів операції згідно з її рішенням i коригування моделей (підвищення їх адекватності).
Після класифікації та спрощення моделей необхідно зробити постановки оптимізаційних задач, відповідно до яких підібрати методи оптимізації. На різних етапах розв’язання оптимізаційної задачі та для різних об’єктів можуть використовуватись різні методи оптимізації. Для статичних або малодинамічних об’єктів це мають бути методи теорії дослідження операцій: лінійного, нелінійного, динамічного, цілочисельного програмування, прямі методи тощо. Для динамічних об’єктів - методи теорії оптимального управління: класичне варіаційне числення, принцип максимуму Л.С.Понтрягіна, метод динамічного програмування Р.Беллмана, метод достатніх умов оптимальності В.Ф.Кротова тощо.