Вопрос 3. Средние величины, их виды.

Средней величиной называется обобщающий показатель, характеризующий типичный уровень изменяющего количественного признака на единицу совокупности в определенных условиях места и времени. Следовательно , рассчитывается средняя величина в вариационном ряду. Ряд, кроме вариантов, содержит в себе частоту. Имеется несколько видов средних:

1. Средняя арифметическая простая - применяется в тех случаях, когда изменяющийся признак (варианта) встречается в совокупности 1 раз.

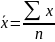
х- изменяющаяся величина (варианта)

п- число единиц.

2. Средняя арифметическая взвешенная - применяется когда изменяющийся признак встречается несколько раз.

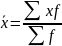
где f – частота (весы),показывает сколько раз встречается изменяющийся признак в совокупности.

3. Средняя гармоническая - применяется, если отсутствуют сведения о частоте.

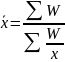
где W=x*f

4. Средняя хронологическая - используется в моментных рядах динамики.

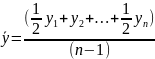
Вопрос 4. Расчет и значение моды в дискретном и интервальном ряду.

Особым видом средних величин являются структурные средние : мода и медиана.

Они применяются для для изучения внутреннего строения изучаемой совокупности.

Мода в статистике –это величина изменяющегося признака (варианты), наиболее часто встречающаяся в совокупности.

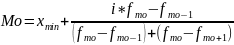
где x_min– нижняя граница модального интервала;

i– величина модального интервала;

f_Mo–частота модального интервала;

f_Mo-1–частота интервала, предшествующего модальному;

f_Mo+1– частота интервала, следующего за модальным.

Мода широко используется в статистической практике при изучении покупательского спроса и регистрации цен и т.д.

Вопрос 5. Расчет и значение медианы в дискретном интервальном ряду.

Медиана представляет собой вариант, находящийся в середине ранжированного (упорядоченного) ряда всех значений признака.

В вариационных рядах мода определяется по наибольшей частоте. Для определения медианы вычисляются накопленные частоты. Медианным будет тот вариант, накопленная частота которого первой превысит половину всех частот. В ранжированном ряду несгруппированных данных номер медианы (если количество единиц нечетное) определяется по формуле

N_ме = (n+1):2

В случае четного объема ряда медиана равна средней из двух вариантов, находящихся в середине ряда.

В интервальном ряду медиана определяется по формуле:

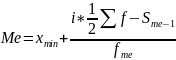
где x_min – нижняя граница медианного интервала (медианный интервал –первый интервал, накопленная частота которого превышает половину общей суммы частот);

i – величина медианного интервала;

S_me-1 – сумма накопленных частот в интервалах, предшествующих медианному;

f_me– частота медианного интервала

Медиана делит всю совокупность на 2 равные по численности части.

Медиана находит практическое применение в маркетинговой деятельности .

Вариационные ряды распределения и оценка вариационного ряда на ассиметрию.

Вариационный ряд распределения — это упорядоченный (ранжированный) перечень статистических показателей, собранных в процессе наблюдения. После ранжирования данных каждой варианте рассчитывают частоту. Ряд распределения располагают в таблицах и изображают графически.

Вариацией называется различие значений признака у отдельных единиц изучаемой совокупности в один и тот же период или момент времени.

Статистический анализ вариации предполагает выполнение следующих этапов работ:

1.Построение вариационного ряда.

2.Графическое изображение вариационного ряда.

3. Расчет показателей центра распределения , структурных характеристик и оценка вариационного ряда на ассиметрию.

4.Расчет показателей размера и интенсивности вариации.

Пример.

1. Приведен упорядоченный вариационный ряд , отражающий распределение жителей города по величине среднедушевого дохода

Среднедушевой доход за месяц тыс. руб	Число жителей чел (f)	Середина интервала (х)	Х*f	Накопленные частоты
До 5	26	2.5	65.0	26
5-10	463	7.5	3472.5	489
10-15	690	12.5	8625.0	1170
15-20	528	17.5	9240.0	1707
20-25	434	22.5	9765.0	-
25-30	350	27.5	9625.0	-
30 и более	318	32.5	10335.0	-
Итого	2809	-	51127.5	-

Частота вариационного ряда- абсолютная численность отдельных единиц в группе (f)

2.Графическое изображение вариационных рядов облегчает их анализ и позволяет судить о форме распределения. Для графического изображения вариационного ряда в статистике строят ГИСТОГРАММУ и КУМУЛЯТУ распределения.

ГИСТОГРАММА-это столбиковая диаграмма для интервального ряда, для дискретного ряда строят ПОЛИГОН РАСПРЕДЕЛЕНИЯ (Соединяют прямыми отрезками точки с координатами Х и W Гистограмма может легко быть преобразована в полигон, если соединить середины верхних сторон прямоугольников отрезками прямых.

КУМУЛЯТА строится по накопленным частотам.

3.Для характеристики среднего значения признака рассчитывают:

Среднюю величину признака

В нашем примере 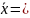51127.5:2809 =18.2 тыс.руб

690-463

М_{о =} 10+5*-----------------------=12.9 тыс. руб

(690-463)+(690-528)

Медиана – это варианта расположенная в середине упорядоченного вариационного ряда.

(2809 :2)-1179

Ме = 15+5---------------------- =17.2 тыс. руб.

528

Следовательно, половина жителей города имеет среднедушевой доход меньше 17.2 тыс. руб, а вторая половина –больше этой суммы.

По соотношению характеристик центра распределения (Среднего значения, моды и медианы) можно судить о симметричности ряда распределения. Симметричным является распределение, в котором частота двух вариантов, равностоящих в обе стороны от центра распределения, равны между собой.

Х = М_о = М_е

Например

Выработка деталей	Число рабочих
2	1
4	2
6	3
8	2
10	1

Правосторонняя асимметрия, т.е. большая часть единиц совокупности имеет значение, превышающее модальное изучаемого признака (X_cp>M_e>M_o)

чел

выработка

Левосторонняя асимметрия - т.е.большая часть единиц имеет значение ниже модального

Чел (X_cp<M_e<M_o)

выработка

Нашему примеру соответствует соотношение Х _ср > М_е > М_о это характерно для правосторонней симметрии (что подтверждает и гистограмма и полигон распределения). 18,2 > 17,2 > 12.9

Наличие правосторонней симметрии свидетельствует о том, что большая часть населения города имеет среднедушевой доход выше, чем его модальное значение 12900 рублей.

Коэффициент ассиметрии, предложенный английским статистиком Пирсоном , определяется по формуле

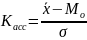
Если значение получится со знаком «+» - правосторонняя симметрия;

«-» - левосторонняя.