2. Индексы индивидуальные и общие (пример расчета).

Индивидуальный индекс показывает изменение изучаемого явления по отдельной единице изучаемой совокупности, например ,изменение цены на отдельный вид товара – молока (i_p), изменение объема продажи молока (i_q):

;

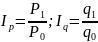Общий (сводный ) индекс дает характеристику изменения изучаемого явления в целом по всей совокупности, это сложный относительный показатель, который бывает в 2-х формах

-агрегатная

-средняя

Основной формой сводного индекса является агрегатная. Агрегатный индекс получается путем сопоставления сложного показателя в отчетном и базисном периодах при помощи соизмерителей (весов).

В числителе и знаменателе агрегатного индекса находится сумма произведений 2-х взаимосвязанных показателей, один их которых анализируется и выступает в роли индексируемой величины, а второй остается неизменным ,т.е. выступает в роли соизмерителя (весов).

Индексируемый показатель записывается в формулу общего индекса первым.

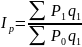
P*Q = товарооборот

Z*Q = Затраты

F*t = Фонд оплаты труда

W*T = Общий выпуск продукции

Первый столбик – качественный показатель, второй – количественный

Если в общем индексе анализируется изменение качественного показателя (P,Z,f,W), то второй сомножитель (q ,T) берется на уровне отчетного периода:

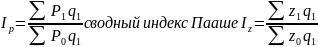
Если в общем индексе изменяется количественный показатель (q ,T), то второй сомножитель (Р) берется на уровне базового периода:

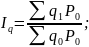
Товарооборот –это общая стоимость проданного товара, она определяется умножением цены на количество проданного товара , т.е.

Т/об=Р*q

Индекс товарооборота

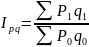
Взаимосвязь индексов 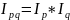Мультипликативная связь

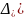Аддитивная модель

2. Индексы переменного, постоянного состава и структурных сдвигов

Индексы переменного состава, постоянного состава и структурных сдвигов используются в экономическом анализе для сопоставления изучаемого явления в отчетном периоде по сравнению с базисным по однородной продукции.

Рассмотрим расчет индексов на примере.

Товар А выпускается в двух цехах.

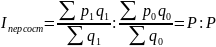
Индекс переменного состава отражает изменение не только индексируемого признака, но и влияние изменения структуры.

Индекс переменного состава показывает изменение среднего значения индексируемой величины.

Индекс постоянного состава показывает среднее изменение цены по изучаемому объекту.

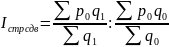
Индекс структурных сдвигов показывает влияние изменения структуры изучаемого объекта на индексируемый показатель (например ,на цену, себестоимость и т.д.)