Раздел 3. Арифметические основы эвм.

Тема 3.1. Система исчисления. Понятие систем исчисления. Система исчисления – совокупность приемов и правил изображение чисел цифровыми знаками.

Системы исчисления (СС) делятся на непозиционные и позиционные.

Непозиционная СС – это система, в которой значение символа не зависит от его положения в числе. Например, римская СС IV – четыре, а VI – шесть. Выполнять арифметические действия в непозиционной СС неудобно, поэтому они не используются в расчетах.

Позиционная СС (ПСС) – это система, в которой значение цифры зависит от её положения в ряду цифр, изображающих число, т.е. веса каждого разряда. Основанием ПСС (p) называют максимальное количество различных цифр, используемых для записи чисел данной ПСС. Например, в десятичной ПСС p=10 – цифры от 0 до 9. 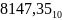(8 – это , 1 –это , 4 это 10, 7 это , 3 это , 5 это ). Т.е. для перевода в двоичную систему: 8* +1* +4*10+7* +3* +5*

При переводе в десятичную из двоичной системы: 1011,01 = 1* +0* +1* +1* +0* +1* = 8+2+1+0,25 = 11,25

Число, записанное в p-ичной ПСС, может быть представлено в следующем виде:

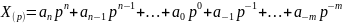
Где - любая цифра, используемая в ПСС;

n, … , -m – номера разрядов числа;

p – основание ПСС – целое положительное число;

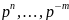- веса разрядов.

В компьютерах применяют ПСС с недесятичным основанием: двоичным, восьмеричным, 16-ричным.

Очевидно, что для человека самой удобной является десятичная ПСС, а для машины – двоичная. Это вызвало появление некоторой смешанной двоично-десятичной системы.

Двоично-десятичное число образуется следующим образом: каждая цифра десятичного числа заменяется четырехразрядным двоичным числом – двоичной тетрадой. Пример:

1964,23 = (заменить двочной тетрадой из таблицы) 0001 1001 0110 0100, 0010 0011

При обратном преобразовании необходимо каждую тетраду заменить эквивалентной ей десятичной цифрой:

010100101000,0100 = (нули добавляются справа от запятой и слева) = 528,4

Перевод чисел из одной сс в другую.

Существует два основных вида перевода чисел из одной СС в другую:

1. Табличный – из понятия СС (очень громоздок): 1011001 = = 1* = 64+16+8+1=89.

2. Расчётный – универсален, но применяется только в ПСС.

   1. Перевод целых чисел из десятичной ПСС в любую другую осуществляется методом деления: 791 = = число делится на 8(под Х), 791/8=98 (98<8? Нет), 98/2=12, 12/8= 1. И записываются остатки = 1427 89= = 1011001

   2. Перевод правильной десятичной дроби в другую ПСС осуществляется методом умножения: 0,125= = умножать на основание СС пока в остатке не будет 0= 0,125*2= 0,250* = 0,500*2 = 1,000 = итого = 0,001(целые числа) 0.718= = 0,718*8= 5,744*8 = 5,952*8 = 7,616 … ~ 0,557

   3. Перевод неправильной дроби десятичной ПСС в любую другую осуществляется в два приема: целая часть переводится по одному правилу, а десятичная – по-другому. Затем целую и дробную части числа записывают вместе, отделяя запятой: 9485,219 = = целая – делением, десятичная – умножением = 9485/16 =...= ~250D; десятичная: 0,219*16=…= ~381. Итого: ~250D,381

Правила преобразования 8-ричных и 16-ричных чисел в двоичные и наоборот просты, т.к. основания 8-ричной и 16-ричной систем есть целые степени числа 2 : 503,7 (в 8-ричной) = перевод в 2-чную = 1010000011, 111 (пишется триадами, потому что 8 – 2 в 3 степепи). 00011111010101100011,11011000 (2чная) = найти 16-ричную = 1F563,В8