1.1.2. Сообщение: дискретная и непрерывная формы

Дискретное сообщение - сообщение, состоящее из отдельных букв или цифр, напр., телеграф­ное сообщение, передаваемое азбукой Морзе (1837). Отдельным элементом такого сообщения м.б. блок цифр, кодирующий буквы или их последовательность, т.е. кодовый блок, напр., 5-элементный код постоянной длины - код Боде (1875).

1.1.2.1. Скорость или частота Найквиста

Дискретные сообщения исследовал Найквист (1924-28), определивший, что по каналу с полосой f_c можно передать максимально 2f_c импульсов/отсчетов в секунду, а для исключения меж-символьной интерференции (МСИ) нужно использовать импульсы вида g*(t) = sin(2f_ct)/(2f_ct) . Вид этой функции (результат прохождения прямоугольного импульса

через идеальный фильтр нижних частот (ФНЧ) с частотой среза f_c ) приведен на рис. 1-2. Ну­-

ли функции g*(t) соответствуют точкам n/2f_c, где n=1,2,3 ..., где достигается максимум функ­ций последовательности, передаваемой со скоростью 2f_c импульсов/с, что исключает МСИ.

Рис.1 -2. Вид импульса, идеального ФНЧ и функции g(t) - результата прохождения импульса через ФНЧ

Частоту 2f_c называют частотой Найквиста, она фигурирует во всех процессах, связанных с дискретизацией аналоговой функции. Функция g*(t) известна также как функция sinc(2f_ct). Она используется в теореме отсчетов.

1.1.2.2. Непрерывное сообщение

Непрерывное сообщение - сообщение, представленное непрерывной функцией времени g(t).

На практике принято считать g(t) функцией с ограниченным частотой _c (_c=2f_c) спектром. Если представить спектр S() этой функции на интервале (-_c, _c) рядом Фурье, а затем вос­становить ее, используя обратное преобразование Фурье, то такая функция м.б. записана в виде суммы отсчетов функции в моменты t_k=kΔt, называемой рядам Котельникова (1933):

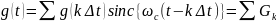. (1 -1)

Слагаемые (1-1) - это отклики 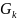идеального ФНЧ с частотой среза 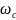(рис. 1-3в) на им­пульс (выборку) (рис. 1-3б), плошадь которого равна значению g(t) в момент 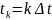. Восста­новление исходной функции (рис.1-3а) на приеме происходит путем пропускания таких им­пульсов, через ФНЧ (рис.1-3г).

Функция 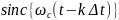интересна тем, что при 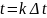она равна 1, а при всех 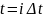для равна 0.Поэтому, даже если выходные импульсы и перекрываются, в моменты, соответст­вующие взятию очередного отсчета значение функции определяется только одним из них.

Если g(t) рассматривается на конечном интервале T, она будет определяться числом выбо­рок m пропорциональным удвоенной верхней частоте среза спектра функции f_c: , т.к. . Итак, можно говорить о справедливости утверждения, известного в мире как теорема отсчетов Найквиста, а у нас как теорема Котельникова.

1.1.2.3. Теоремы отсчетов Котельникова и Найквиста

Теорема Котельникова:

Функция g(t) с ограниченным частотой спектром вполне определяется своими мгновенны­ми значениями g(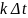 ),отсчитанными через интервал 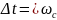, и м.б. представлена рядом вида (1-1).

Теорема отсчетов Найквиста:

По Шеннону: Сигнал g(t) с шириной полосы частот В м.б. восстановлен по его отсчетам. взятым со скоростью Найквиста 2В, путем использования интерполяционной формулы вида:

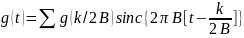. (1-2)

Замечания о теоремах Найквиста и Котельникова Теоремы Найквиста-Котельникова широко ис­пользуются на практике в системах передачи данных (СПД). В их упрошенных формулиров­ках часто опускают то, что они справедливы только для функций с ограниченным частотой f_c спектром. Однако сигналы в сетях связи имеют широкий спектр, что нужно учитывать на практике и, если нужно, использовать фор­мирующие фильтры.

Так, канал тональной частоты (КТЧ), ис­пользуемой в телефонных сетях (ТфОП), имеет верхнюю частоту среза 3,4 кГц, хотя ширина спектра голоса м.б. до 16-20 кГц. Чтобы удов­летворить требованию ограниченности спектра на практике, АЧХ дискретизируемого сигнала формируют путем пропускания сигнала через ФНЧ с частотой среза f_c=4 кГц. Такие фильтры устанавливаются в аналого-цифровых преобра­зователях (АЦП) цифровых систем связи. В этом случае в качестве расчетной частоты среза используют 4 (а не 3,4) кГц, а 0,9 (4-3,1=0,9) кГц рассматривается при этом как переходная полоса КТЧ.