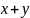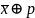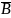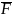Указать возможные пути “склеивания” по методу кубов.
x |
y |
z |
|
0 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
Решить задачу синтеза ркс.
Часть 2. Тема: “Доказательство теорем. Нечеткая логика”.
Формализовать теорему:
Если собака лает или спит, то она не кусает, если же она кусает и не спит, то, либо собака не лает, либо потерпевший глух. Пусть собака кусает в том и только в том случае, когда потерпевший глух. Верно ли, что собака кусает и потерпевший глух
Заключение
В: Верно ли, что собака кусает и потерпевший глух.
Аксиомы
А1: Если собака лает или спит, то она не кусает
А2: Если же она кусает и не спит, то, либо собака не лает, либо потерпевший глух
Гипотеза
Г1: Пусть собака кусает в том и только в том случае, когда потерпевший глух.
Атомы
x: лает
y: спит
z: кусает
p: потерпевший глух
А1:
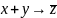
А2: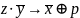
Г1:
В:
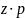
F=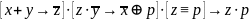
Доказать или опровергнуть теорему, формализованную в результате выполнения задания 1, используя метод таблиц истинности.
x |
y |
z |
p |
|
|
А1 |
|
|
|
|
А2 |
Г1 |
|
|
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
