Лекции 17 - 18. Цифровые фильтры

1. Трансверсальные (нерекурсивные) цифровые фильтры

Алгоритм работы трансверсального (поперечного) цифрового фильтра можно описать с помощью формулы

, (1)

где  - время задержки входного сигнала в одном звене фильтра, X(t) – входной сигнал, Y(t) –выходной сигнал, a_i – коэффициенты фильтра.

Согласно (1) выходное напряжение трансверсального фильтра равно взвешенной сумме n+1 входных напряжений, каждое из которых задержано на целое число тактов . Число n элементов задержки в (1) определяет порядок цифрового фильтра.

Рис.1. Схема трансверсального (нерекурсивного) цифрового фильтра n-го порядка.

Расчет комплексного коэффициента передачи трасверсального фильтра n-го порядка

Представим входной и выходной сигналы в виде интегралов Фурье

- 109 -

. (1) . (2)

где S_X(f) и S_Y(f) – спектральные плотности входного и выходного сигналов X(t) и Y(t).

Выходное напряжение фильтра n-го порядка согласно (1) и (2)

. (3)

Анализ (2) и (3) показывает, что задержка сигнала X(t) на один такт T= эквивалентна умножению X(t) на множитель

.

Подобная операция получила название Z-преобразования сигнала.

Из (3) комплексный коэффициент передачи нерекурсивного ЦФ n-го порядка равен

. (4)

Из (4) видно, что комплексный частотный коэффициент передачи трансверсального фильтра n-го порядка представляет собой периодическую функцию по частоте. Период изменения коэффициента передачи по частоте  равен

Расчет ачх и фчх трансверсального фильтра первого порядка

Согласно (4) комплексный коэффициент передачи фильтра первого порядка равен

. (5)

- 110 -

Рис.2. Схема трансверсального цифрового фильтра первого порядка.

Расчет цифрового фильтра сводится к определению коэффициентов a_i в соответствии с требуемым комплексным коэффициентом передачи. Положим

. (6)

Из (5) получаем

. (7)

Найдем АЧХ трансверсального ЦФ первого порядка. Для этого используем формулу Эйлера

. (9)

Наибольший интерес для практических приложений представляют случаи a₁=1 и a₁=-1. Соответствующие этим случаям АЧХ представлены на рис.3 и 4. Как видно из приведенных АЧХ, подобные схемы могут быть использованы как гребенчатые режекторные (подавляющие) фильтры.

Рис.3. АЧХ трансверсального фильтра 1-го порядка при a1=1. Реализован гребенчатый режекторный фильтр для частот f=1/2T+k/T , где k = 0, 1, 2…ФНЧ.

Рис.4. АЧХ трансверсального фильтра 1-го порядка при a1=-1. Реализован гребенчатый режекторный фильтр для частот f=k/T, где k = 0, 1, 2,… ФВЧ.

- 111 -

Фазово-частотная характеристика трансверсального ЦФ первого порядка может быть найдена из (8) путем преобразования экспоненты по формуле Эйлера.

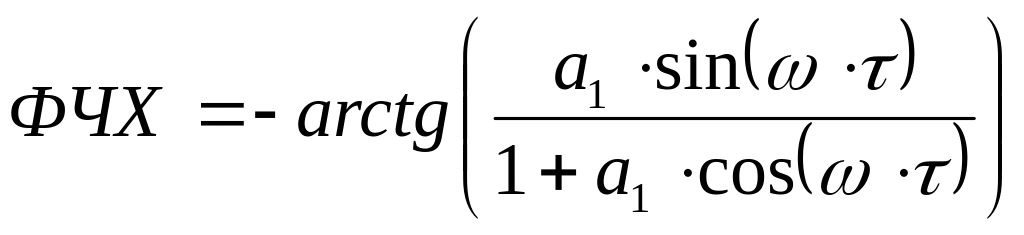. (10)

Расчет ачх и фчх трансверсального фильтра второго порядка

Рис.5. Схема трансверсального (нерекурсивного) цифрового фильтра второго порядка.

Согласно (4) комплексный коэффициент передачи фильтра второго порядка равен

. (6а)

Положим, что . Из (6а) получаем

. (7а)

Найдем АЧХ трансверсального ЦФ второго порядка для наиболее интересного частного случая a₂=1. Учтем, что . Из (7а) имеем

. (8а)

- 112 -

Особенностью трансверсального ЦФ второго порядка при a0=a2=1 является возможность перестраиваемой с помощью a₁ режекции на любой из частот рабочего диапазона.

Наибольший интерес для практических приложений представляют случаи a₁=2, a₁=0 и a₁=-2.

Рис.6. АЧХ трансверсального ЦФ второго порядка. a0=1, a2=1, a1=2. Реализован ФНЧ.	Рис.7. АЧХ трансверсального ЦФ второго порядка. a0=1, a2=1, a1=-2. Реализован ФВЧ
Рис.8. АЧХ трансверсального ЦФ второго порядка. a0=1, a2=1, a1=0. Режекторный фильтр на частоте f=1/(4T).	Рис.9. АЧХ трансверсального ЦФ второго порядка. a0=1, a2=1, a1=1. Режекторный фильтр на частоте f=3/(8T).

Фазово-частотная характеристика трансверсального ЦФ второго порядка может быть найдена из (7а) путем преобразования экспонент по формуле Эйлера

- 113 -

. (9а)