Контрольная работа 2 / Контрольная №3 по Т.О.Э. вар 18

11

Министерство образования и науки Российской Федерации

Факультет дистанционного обучения (ФДО)

Томский государственный университет систем

управления и радиоэлектроники

(ТУСУР)

Кафедра промышленной электроники (ПрЭ)

Контрольная работа № 3

Расчёт цепи синусоидального переменного тока

по дисциплине: «Теоретические основы электротехники-1»

Вариант 18

Выполнил:

Студент ФДО гр.

________________

« ___ » ____________2010г.

Проверил:

________________

« ___ » ____________2010г.

2010

Содержание

1 ЗАДАНИЕ И ИСХОДНЫЕ ДАННЫЕ

В контрольной работе необходимо выполнить следующее задание:

1. Составить в общем виде уравнения электрического равновесия цепи по законам Кирхгофа, методом контурных токов (МКТ), методом узловых потенциалов (МУП). Одним из этих методов по выбору студента рассчитать токи всех ветвей. Осуществить проверку расчётов балансом активной и реактивной мощностей.

2. Методом эквивалентного генератора определить ток в ветви с источником э.д.с.

3. Построить точную векторную диаграмму напряжений цепи.

4. Записать мгновенное значение тока через источник э.д.с.

Параметры источников и сопротивлений заданы в таблице 1.1 согласно шифру.

Таблица 1.1

, В	, А	,	, Ом	, Ом	, Ом	, Ом
45	0.2	628	400	0	300	200	14 мкФ	0.5 Гн	0	0

По данным таблицы 1.1 из обобщённой схемы [1] формируется индивидуальная схема, показанная на рисунке 1.1.

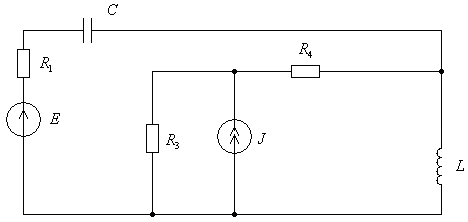
Рисунок 1.1 – Схема исследуемой цепи

2 РАСЧЁТНАЯ ЧАСТЬ

2.1 Уравнения электрического равновесия по законам Кирхгофа

Для вывода уравнений укажем направления протекания токов в ветвях и обозначим замкнутые контура, используемые для составления уравнений по 2-му закону Кирхгофа, что и представлено на рисунке 2.1.

Рисунок 2.1

В соответствие с рисунком 2.1 число узлов , а число ветвей . Следовательно, первый закон Кирхгофа позволяет составить линейных уравнений, а второй закон Кирхгофа: линейных уравнений.

Составим систему уравнений по первому закону Кирхгофа:

1

2

3

Составим систему уравнений по второму закону Кирхгофа:

I

II

Перейдём к комплексным значениям сопротивлений и комплексным источникам:

Ом,

Ом.

Схема в комплексном виде приобретает следующий вид, представленный на рисунке 2.2.

Рисунок 2.2

Соответственно система уравнений по первому закону Кирхгофа:

1

2

3

Систему уравнений по второму закону Кирхгофа:

I

II .

2.2 Расчёт цепи методом контурных токов

Число независимых уравнений по МКТ равно числу уравнений, которые мы составляли по второму закону Кирхгофа и равно 2. Выбираем направления контурных токов и путь протекания тока источника тока, что и представлено на рисунке 2.3.

Рисунок 2.3 – Схема цепи для решения по методу контурных токов

Составим систему уравнений:

I

II

Подставляем численные значения величин и находим контурные токи:

,

,

,

А.

А.

По контурным токам найдём токи в ветвях:

А;

А;

А;

А.

2.3 Расчёт цепи методом узловых потенциалов

Пронумеруем узлы и заземлим узел номер 0, что и представлено на рисунке 2.4.

Рисунок 2.4 – Схема цепи для решения по МУП

Составим систему уравнений:

для узла 1:

для узла 2:

.

См,

См,

См.

Подставляем в исходную систему найденные значения проводимостей

Из первого уравнения получим:

.

Подставим выражение для во второе уравнение и найдём :

.

Разрешая это уравнение относительно неизвестного получим:

В.

Находим :

В.

По закону Ома определяем токи в ветвях:

А;

А;

А;

А.

2.4 Проверка расчётов балансом активной и реактивной мощностей

Вычислим комплекс:

.

Активная мощность источников:

Вт.

Реактивная мощность источников:

Вар.

Активная мощность нагрузок:

Вт.

Реактивная мощность нагрузок:

Вар.

Из результатов расчётов видно, что с учётом погрешностей вычислений баланс активной и реактивной мощностей выполняется.

2.5 Расчёт тока в ветви с источником э.д.с. методом эквивалентного генератора

Для определения параметров эквивалентного генератора напряжения в исходной схеме (рис. 2.2) отключим ветвь с , таким образом, получим в результате схему на рис. 2.5.

Рисунок 2.5 - Схема для расчёта эквивалентного генератора, при удалении ветви с

Э.д.с. эквивалентного генератора равна напряжению между точками 0 и 2. Для её вычисления воспользуемся МУП:

Составим систему уравнений:

для узла 1:

для узла 2:

.

См,

См,

См.

Подставляем в исходную систему найденные значения проводимостей:

Из первого уравнения получим:

.

Подставим выражение для во второе уравнение и найдём :

.

Разрешая это уравнение относительно неизвестного получим:

В.

Находим :

В.

Напряжение эквивалентного генератора:

В.

Внутреннее сопротивление эквивалентного генератора определяем, исключив из схемы (рисунок 2.5) источник тока и источник напряжения, т.е. по схеме на рисунке 2.6.

Рисунок 2.6 - Схема для нахождения внутреннего сопротивления эквивалентного генератора

Ом.

Искомый ток :

А.

2.6 Построение векторной диаграммы напряжений

Диаграмму строим для схемы на рисунке 2.2. Рассчитаем напряжение на всех элементах схемы, взяв значения токов в ветвях, определённых по методу контурных токов:

В;

В;

В;

В;

В.

Диаграмма представлена на рисунке 2.7.

Рисунок 2.7 – Векторная диаграмма напряжений

Порядок построения её следующий. Из начала координат в выбранном масштабе по оси +1 отложен вектор (так как начальная фаза источника э.д.с. равна нулю).

Так же из начала координат под углом проведён вектор , затем из его конца под углом проведён вектор . Из конца вектора под углом проведён вектор . По второму закону Кирхгофа сумма напряжений на , и должна равняться приложенной э.д.с. (при обходе по внешнему контуру схемы, см. рисунок 2.2). Поэтому концы векторов и совпали.

В схеме есть ещё один контур (содержит элементы , , , ). Для этого контура первые два вектора, а именно и , уже построены. Из конца вектора под углом проведён вектор и аналогично далее под углом вектор . Конец вектора совпал с концом вектора .

Векторная диаграмма, таким образом, позволяет произвести проверку выполненных расчётов (несовпадение векторов , и указало бы на неправильный расчёт цепи).

2.6 Мгновенное значение тока через источник э.д.с.

Запишем получившееся действующее значение искомого тока через источник э.д.с.:

А.

Перейдём к тригонометрической форме записи:

А.

Запишем мгновенное значение искомого тока:

А.

Список используемой литературы

1. Коновалов Б.И. Теоретические основы электротехники: Учебное методическое пособие. — Томск: Томский межвузовский центр дистанционного образования, 2006. — Ч.1. — 75 с.

2. Коновалов Б.И. Теоретические основы электротехники: Учебное пособие. — Томск: Томский межвузовский центр дистанционного образования, 2006. — Ч.1. — 145 с.