Инвариантность формы первого дифференциала
Правило дифференцирования сложной функции приведет нас к одному замечательному и важному свойству дифференциала.
Пусть
функции
и
таковы, что из них может быть составлена
сложная функция:
.
Если существуют производные
и
,
то существует и производная
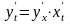
Перейдём теперь к независимой переменной ; в этом предположении имеем другое выражение для дифференциала:
.
Заменяя
производную
её выражением и замечая, что
есть дифференциал
как функции от
,
окончательно получим:
,
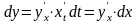т. е. вернёмся к прежней форме дифференциала.
Таким образом, мы видим, что
форма дифференциала может быть сохранена даже в том случае, если прежняя независимая переменная заменена новой.
Мы
всегда имеем право писать дифференциал
как в форме (1), будет ли
независимой переменной или нет; разница
лишь в том, что, если за независимую
переменную выбрано
,
то
означает не произвольное приращение
,
а дифференциал
как функции от
.
Это свойство и называют инвариантностью
формы дифференциала.
Дифференциал суммы, произведения и частного функций.
Из любой формулы для производной в точке x при умножении на dx
получается соответствующая формула для дифференциала. В частности, в точках,
где функции u, v удовлетворяют условиям теорем о дифференцируемости суммы,
произведения или частного получаем: d(u+v)=du+dv;
аналогично, d(uv)=vdu+udv, d(u/v)=(vdu-udv)/v2.
Отметим, что если C – постоянная, то dC=0, dCu=Cdu.
ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ ВЫСШИХ ПОРЯДКОВ
Последовательные производные
Производная
функции f,
в свою очередь, может иметь производную.
Последнюю в этом случае называют второй
производной
(или производной
второго порядка)
функции f
и обозначают обычно
.
Таким образом,
.
В соответствии с этим
называют первой
производной
(или производной
первого порядка)
функции f.
По индукции определяют (в предположении,
что они существуют) производные следующих
порядков: f´´´
= (f´´)´
и т.д. Если f
имеет n-ю
производную (а значит, и производные
всех меньших порядков) во всех точках
некоторого промежутка I,
то говорят, что f
n
раз (или n-кратно)
дифференцируема на промежутке I.
Функцию f,
имеющую на I
производные всех порядков, называют
бесконечно
дифференцируемой
на I.
Таковы, например, на всем множестве
действительных чисел алгебраические
многочлены, показательные функции.
Для обозначения порядка производной, если он невелик, используют также римские цифры. Так, fIV – четвертая производная функции f. Вообще же, n-ю производную функции f обозначают f(n) (в частности, f(1) = f´). При этом удобно саму функцию f обозначать символом f(0). В таких обозначениях, очевидно, f(n) = (f(k))(n-k) для всех k, 0≤k≤n.
Итак,
функция f
имеет в точке x0
(a,b)
производную f(n)(x0)
(обозначение: f
D(n)(x0))
в том и только в том случае, когда в
некоторой окрестности
точки
x0,
(a,b),
существуют производные функции f(k)
всех порядков
,
и функция f(n-1)
имеет в x0
производную (f(n-1))´(x0)
= f(n)(x0).
Для некоторых бесконечно дифференцируемых функций легко указать формулу для вычисления n-ой производной.
Примеры
1)
f(x)
= xα,
x>0,
α
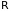- фиксировано. Имеем: f(k)(x)
= α(α-1)…(α-k+1)xα-k,
x>0,
.
Если α
= n
,
то f(x)
= xn
определена на всем
и (xn)(k)
= n(n-1)…(n-k+1)xn-k,
x
,
1≤k≤n-1.
При
получим (xn)(n)
=
для всех x
(так как (xn)(n-1)
= n!x,
x
),
и поэтому (xn)(m)
= 0
для всех x
и всех
.
2) f(x) = ex, x . Поскольку f´(x) = ex, f´´(x) = ex, то f(k)(x) = ex, x , k .
3) f(x) = sinx, x . f(k)(x) = sin(x+k ), x , k .
4) f(x) = cosx, x . f(k)(x) = cos(x+k ), x , k .
5) f(x) = (1+x)α, x>-1, α - фиксировано. f(k)(x) = α(α-1)…(α-k+1)(1+x)α-k, x>-1, k .
6)
f(x)
= ln(1+x),
x>-1.
f(k)(x)
=
,
k
.
Линейное свойство производных высших порядков
Теорема.
Для
любого числа
,
любых функций u
и v,
имеющих в какой-то точке x
производные u(n)(x)
и v(n)(x),
и для любых чисел λ1,λ2
,
функция w
= λ1u
+ λ2v
имеет в точке x
производную w(n)(x)
и w(n)(x)
= (λ1u(x)
+ λ2v(x))(n)
= λ1u(n)(x)
+ λ2v(n)(x).
N-Я ПРОИЗВОДНАЯ ПРОИЗВЕДЕНИЯ
Теорема (Г. Лейбниц). Если функции f и g на некотором промежутке имеют производные функции f(n) и g(n), n , то существует (fg)(n) и
(fg)(n)
=
= fg(n)
+ nf´g(n-1)
+ … +
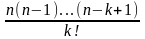f(k)g(n-k)
+ … + nf(n-1)g´
+ f(n)g.
ВТОРАЯ ПРОИЗВОДНАЯ ФУНКЦИИ , ЗАДАННОЙ ПАРАМЕТРИЧЕСКИ
Рассмотрим уравнение
где , − дважды дифференцируемые функции на некотором промежутке ; пусть, кроме того, функция строго возрастает (или убывает) на и ни в одной точке этого промежутка не равна 0. В пункте 20.7 доказано, что в этом случае уравнения (2) задают функцию , и производная этой функции равна
Бывает
также, что производные по параметру
обозначают так:
,
.
Тогда формула (3)
принимает вид:
.
Найдём вторую производную функции
:
ДИФФЕРЕНЦИАЛЫ ВЫСШИХ ПОРЯДКОВ
Однородную линейную функцию называют линейной формой.
Напомним, что если функция дифференцируема в точке , то
дифференциалом в x называют линейную форму .
Аналогично, если дифференцируема дважды в точке ,
то
ее вторым
дифференциалом называют
квадратичную форму
.
Вообще, n-ым дифференциалом в точке x будет n-ичная
форма
(в предположении, что
существует).
Для
n-го
дифференциала
в точке x
используют обозначение
или, более
строго
.
Таким образом, по определению,
= для всех .
Согласно
этому определению,
есть
n-я
степень функции
и
потому
используют обозначение
.
Тогда
для
всех
,
или
.
Форма записи n-го дифференциала не инвариантна
уже при n=2. Действительно, подставляя вместо дифференцируемую
функцию
в левую часть формулы (при n=2),
получим
=
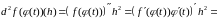
а в результате такой же подстановки в правую часть, имеем
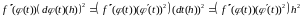.(5)
Правые
части этих формул отличаются слагаемым
.
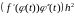Вообще говоря, это слагаемое не равно нулю. Однако если - линейная функция,
то
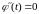и, вообще, для любого
имеет место равенство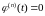
,
откуда следует, что формула будет верна и для линейной функции .