Раздел 3. Элементы дифференциального исчисления

• Излагаются основные свойства производных и дифференциалов функций

• Рассматриваются вопросы дифференцируемости функций одной и нескольких переменных

ПРОИЗВОДНАЯ, ЕЁ СМЫСЛ И ОСНОВНЫЕ СВОЙСТВА. ДИФФЕРЕНЦИРУЕМОСТЬ ФУНКЦИИ

Пусть 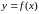определена в окрестности точки .

Определение. Числовую функцию называют дифференцируемой в точке , если для всех имеет место равенство

,

где число не зависит от , а при 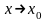и бесконечно малая функ­ция непрерывна в точке , т.е. .

Числовую функцию называют дифференцируемой на множестве , если дифференцируема в каждой точке .

Теорема. Функция , дифференцируемая в точке , непрерывна в этой точке.

Пример функции 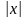(эта функция не дифференцируема в точке ), показывает, что утверждение, обратное теореме, неверно.

Производная

Пусть определена в окрестности точки .

По­скольку на множестве определена функция и - предельная точка для , то можно ставить вопрос о существовании предела разностного отношения в точке .

Определение. Число (если оно существует) называют производной функции в точке и обозначают символом .

Итак,

,

при условии, что предел существует.

Для обозначения производной также используется символ .

Скорость прямолинейного дви­жения есть производная перемещения как функции времени. Часто полез­но, по аналогии с этим, трактовать и производную любой функции в точке как скорость изменения функции в этой точке.

Пример. Линейная функция имеет производную в каждой точке, и ее производная - постоянная. В частности, постоянная имеет всюду производную, равную нулю, а то­ждественная функция - производную, равную единице.

Пример. Квадратичная функция имеет производную в каждой точке, и ее производная равна .

Пример. Модуль не имеет производной в точке 0.

В этом примере мы встретились с ситуацией, когда существуют и . Эти величины называются, соответственно, правой и левой производной и обозначаются . Для существования производной необходимо и достаточно, чтобы существовали и были равны друг другу.

Теорема. Функция , дифференцируемая в точке , имеет в этой точке производную, и последняя равна коэффициенту .

Теорема показывает, что функция , дифференцируемая в точке , представима в виде

,

где при .

Теорема. Функция , имеющая производную в точке , дифференци­руема в этой точке.

Таким образом, сказать, что числовая функция дифференцируема в дан­ной точке, или что она имеет в этой точке производную, одно и то же. Нахо­ждение производной функции у функции называют дифференцировани­ем этой функции.

Касательная к графику функции

Как и нахождение скорости неравномерного движения, нахождение ка­сательной к кривой линии - одна из основных задач, решение которых при­вело к созданию дифференциального исчисления.

Рассмотрим частный случай задачи о касательной, когда линией служит график функ­ции.

О пределение. Пусть числовая функция определена на невырожден­ном промежутке 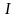и непрерывна в его точке (так что расстояние от соответствующей точки 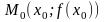графика до его точки , , 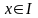стремится к нулю при ) . Касательной к графику функции в точке 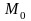называют такую прямую, проходящую через , что отношение расстояния от точки до этой прямой к расстоянию от до стремится к нулю при (т.е. что бесконечно мало по сравнению с при ).

Таким образом, кривая, обладающая в точке каса­тельной, почти сливается с ней вблизи этой точки.

Теорема. Если функция , определенная на промежутке, дифференци­руема в его точке , то график этой функции имеет в соответствующей точ­ке касательную, причем угловой коэффициент касательной равен .

Таким образом, нахождение углового коэффици­ента касательной (как и нахождение скорости) при­водит к вычислению производной.Уравнение касательной имеет вид

Замечание. Секущая имеет угловой коэффициент (см. рис. 15). Таким образом теорема показывает, что угловой коэффициент ка­сательной в точке есть предел углового коэф­фициента секущей при .

ПРАВИЛА ДИФФЕРЕНЦИРОВАНИЯ

Дифференцирование линейной комбинации, произведения и ча­стного

Напомним, что линейной комбинацией функций называют всякую функцию , представимую в виде , где коэффициенты - постоянные. Областью ее определения служит пересечение областей оп­ределения функций . Из теорем 19.5 и 19.6 следует

Теорема (линейное свойство операции дифференцирования). Если функции дифференцируемы в точке , то всякая линейная комбинация этих функций дифференцируема в точке , причем

.

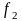Теорема. Если функции и дифференцируемы в точке , то их произведение дифференцируемо в точке , причем

.

Теорема. Если функции и дифференцируемы в точке , и то их частное дифференцируемо в точке , причем

.

Предельные величины

Пусть обозначает величину издержек производства, рассматриваемую, как функцию от количества выпускаемой продукции. Если прирост продукции, приращение издержек производства , то 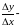среднее приращение издержек производства на единицу продукции. Производная выражает предельные издержки производства и является приблизительной характеристикой дополнительных затрат на производство единицы дополнительной продукции.

Вполне аналогично определяются предельная выручка, предельный доход, предельная полезность и т.п.

Предельные величины также часто называют маржинальными .

ПРОИЗВОДНЫЕ ЭЛЕМЕНТАРНЫХ ФУНКЦИЙ, ПРОИЗВОДНАЯ ОБРАТНОЙ ФУНКЦИИ, ПРОИЗВОДНАЯ СЛОЖНОЙ ФУНКЦИИ, ПРОИЗВОДНАЯ ФУНКЦИИ, ЗАДАННОЙ ПАРАМЕТРИЧЕСКИ

1.Производная степенной функции 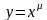, равна

.

В частности

если , то

если , то .

2.Производная показательной функции ( , ).

.

В частности,

если , то и .

Итак, скорость возрастания показательной функции ( при ) пропорциональна значению самой функции: чем большего значения функция уже достигла, тем быстрее в этот момент она растёт.

3. Производная логарифмической функции ( , ). В этом случае

.

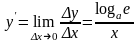В частности, для натурального логарифма получается исключительно простой результат:

при имеем .

Это даёт (хотя, по существу, и не новое) основание для предпочтения, которое оказывается натуральным логарифмам при теоретических исследованиях.

4.Производные тригонометрических функций. Пусть , тогда

.

Аналогично найдём:

если 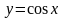, то .

В случае

Аналогично,

если , то .