
Оптимизация с дискретным временем
1. Динамическое программирование
Система
наблюдается в моментах времени

Состояние
системы характеризуется числом
 .
Известно значение
.
Известно значение
 .
Система
меняет своё состояние под воздействием
управлений
.
Система
меняет своё состояние под воздействием
управлений
 ,
которые можно свободно выбирать из
заданного множества
,
которые можно свободно выбирать из
заданного множества
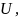 которое назовём областью
управления.
Управления
влияют на состояния системы по правилу
которое назовём областью
управления.
Управления
влияют на состояния системы по правилу
 ,
(1)
,
(1)
где
 – заданная функция.
– заданная функция.
Предположим,
что выбраны величины
 .
Тогда,
начиная с
.
Тогда,
начиная с
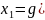 ),
далее получим
)
и т.д.
),
далее получим
)
и т.д.
Таким образом, каждому выбору управлений соответствует свой путь (или график).
Пусть
имеется функция
 такая, что польза от выбранного пути
есть сумма:
такая, что польза от выбранного пути
есть сумма:

![]() (*)
(*)
Эта сумма носит название целевой функции.
Иногда
вместо

![]() пишут
пишут
 .
.
Вместе
с любой заданной последовательностью

![]() находим последовательность
находим последовательность

![]() и получаем соответствующие допустимые
пары.
При этом целевая функция принимает
определенное значение.
и получаем соответствующие допустимые
пары.
При этом целевая функция принимает
определенное значение.
Задача
состоит в том, чтобы среди всех наборов
допустимых пар
![]() и
найти оптимальный
набор пар
и
найти оптимальный
набор пар
![]()
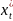 ,
, ,
дающий наибольшее значение целевой
функции.
,
дающий наибольшее значение целевой
функции.
Задача, в краткой формулировке, записывается так:
найти

 при условиях
при условиях
![]() ,
задано,
(2).
,
задано,
(2).
Рассмотрим пример реальной задачи, которая решается по изложенной выше схеме.
Пусть

![]() средства в момент
средства в момент
 В каждый момент
В каждый момент
 пусть
пусть

![]() часть, используемая для потребления,
часть, используемая для потребления,
![]()
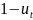 –
часть для сбережения. Средства можно
употребить в дело с уровнем прироста
–
часть для сбережения. Средства можно
употребить в дело с уровнем прироста
 .
После изъятия
ко
.
После изъятия
ко![]() личества
средств
личества
средств
 ,
остаток средств
,
остаток средств идёт в дело
идёт в дело![]() .
При этом, с учётом прироста, получаем
.
При этом, с учётом прироста, получаем
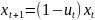
![]() .
.
Пусть
польза от потребления
 равна
равна
 .
.
Пусть
функция
 возрастает и выпукла вверх по
возрастает и выпукла вверх по .
.
Вся полученная польза равна:

Итак, решается задача:
Найти
 при условиях
при условиях

 задано,
задано,
 ,
, .
.
2. Свойства целевой функции.
Пусть
при
 система имеет значение x.
Наилучшее, что можно сделать в оставшийся
период – выбрать
система имеет значение x.
Наилучшее, что можно сделать в оставшийся
период – выбрать
 (следовательно,
(следовательно,
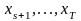 )
так, чтобы максимизировать
)
так, чтобы максимизировать
 при
при
 .
.
Назовем оптимальной целевой функцией для этой задачи в момент s.
 (3)
(3)
где
,
 ,
,
 ,
,
 (4)
(4)
Управления,
максимизирующие (3) при условиях (4),
зависят от х.
В частности,
 зависит от х.
зависит от х.
![]() Управления, зависящие от состояния
системы назовем политиками.
Управления, зависящие от состояния
системы назовем политиками.
Если
мы напишем для каждого![]() политику, то мы тем самым решили задачу
(2)
политику, то мы тем самым решили задачу
(2)
Рассмотрим
важное свойство целевой функции.
При![]() имеем
имеем
![]() .
.
Пусть
при ![]() система
в состоянии
система
в состоянии ![]() .
При выборе
.
При выборе ![]() при
при ![]() получен выигрыш
получен выигрыш ![]() ,
при этом система окажется в состоянии
,
при этом система окажется в состоянии
![]()
При
этом наибольший полный выигрыш, который
можно получить от ![]() до
до![]() ,
начиная с состояния
,
начиная с состояния ![]() ,
равен
,
равен ![]()
Следовательно,
наилучшим выбором для![]() будет
то, которое максимизирует сумму
будет
то, которое максимизирует сумму ![]()
Теорема:
Пусть![]() обозначает
целевую функцию в момент
обозначает
целевую функцию в момент ![]()

![]() ,
,
![]() ,
,
![]()
для задачи найти:
|
(5) |
при
условиях
,
![]() – задано,
– задано, ![]()
Тогда![]() удовлетворяет
уравнениям
удовлетворяет
уравнениям
|
(6) |
![]()
|
(7) |
Замечание:
Разумеется значения
выбираются среди решений разностного
уравнения (1) при фиксированном
и возможных выборах ![]() .
.
Обычно эта теорема используется так: ищем функцию (7).
Максимизируются значение U*T (x). Следующий шаг – используя (6) найти JT-1(x) и соответствующую W*T-1(x). Действуя аналогично, находим все JT (x), JT-1(x),….,J0(x) и соответствующие U*T(x), U*T-1(x),…,U*0(x).
Это позволяет построить решение исходной задачи оптимизации.
Пример.
Рассмотрим задачу найти:
max
 ,
при условиях
,
при условиях
 ,
t=0,
1, 2,
,
t=0,
1, 2,
 ,
, .
.
Здесь T=3, f(t,x,u)=1+x-u2 , g(t,x,u)=x+u.
Из
(7) при T=3получаем,
что J3(x)
представляет собой наибольшее значение
функции
 ,
,
 .
.
Оно
получается при u=0,
т.е. J3(x)=1+x,
 .
.
При s=2 функция максимизируется, обозначим ее h2(u)=1+x-u2+J3(x+u)
Так как J3(x)=1+x, J3(x+u)=1+(x+u) и h2(u)=1+x-u2+1+x+u=2+2x+u-u2; h2’(u)=1-2u, h2’(u)=0, u=1/2, h2(u) выпукла вверх, то u, u2*(x)=1/2, J2(x)=h2(u2*(x))=2+2x+1/2-1/4=2x+9/4.
При s=1 мы максимизирует функцию h1(u)=1+x-u2+2(x+u)+9/4=3x+2u-u2+13/4
h1’(u)=2-2u; h1’(u)=0, u=1.
Находим u1*(x)=1 и J1(x)=3x+2-1+13/4=3x+17/4.
При s=0 максимизируется функция
![]() .
.![]()
![]()
![]()
![]()
Укажем оптимальные значения состояния системы:
![]()
![]()
![]()
Оптимальное значение целевой функции:
![]()
.
В простых случаях, подобных рассмотренному, задача динамической оптимизации допускает решение с использованием обычных методов анализа.
Полагая в уравнении


последовательно получаем


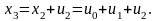
Таким образом, максимизация целевой функции равна





![]()
 -
матрица 2 дифференциала
-
матрица 2 дифференциала
По критерию Сильвестра второй дифференциал – отрицательно определенная форма следовательно получаем тоже максимум
Подобный подход возможен в любой задаче, но он слабо реализуем при больших T.
Рассмотрим еще одну задачу :
Найти
max
при
условии ![]()
Поскольку
![]() и
и
![]() для
для ![]() t
выполняется неравенство
t
выполняется неравенство ![]()
Далее
, ![]() независимо от u
, и поэтому
независимо от u
, и поэтому ![]() и любое решение
и любое решение ![]() оптимальнее
оптимальнее
Уравнение
(1) при S=T-1
дает ![]()
Первая
производная по u
функции ![]() равна
равна
![]() ,
,
1+ux=3/2, ux=1/2.
![]()
При
этом![]() .
.
Итак,
![]() (
(![]() )
)
![]()
Рассмотрим
уравнение (6)
при
![]()
![]()
Снова получаем
![]() ,
,
при
этом ![]()
Очевидно, что далее, продолжая процесс, получим
![]()
Подстановка
![]() в
разностное уравнение дает
в
разностное уравнение дает![]() =
=![]()
При
этом .
.
Примечание
Теорема
справедлива и в том случае, когда область
управления не фиксирована, но зависит
от![]() и
и
![]() ,
,
![]() .
Тогда максимизация в (2), (3), (5) выполняется
при
.
Тогда максимизация в (2), (3), (5) выполняется
при ![]() .
В (6)(стр. 7),(7)(стр. 7) максимизациявыполняется
при
.
В (6)(стр. 7),(7)(стр. 7) максимизациявыполняется
при ![]() и
и ![]() ,
соответственно.
,
соответственно.
Часть
множеств ![]() задается набором неравенств
задается набором неравенств![]() .
.
Если
-
пустое множество, то принимается
соглашение, по которому максимум взят
по этому множеству равен -![]() .
.
Рассмотрим задачу, в которой
 =
=
 (
( -
),
> 0,
- заданные положительные числа
-
),
> 0,
- заданные положительные числа
β
=
 , r
– уровень дисконтирования, 0 <
<
, γ
, r
– уровень дисконтирования, 0 <
<
, γ (0, 1), A>0
(0, 1), A>0
Ищется
max
( +
+
 ) (I)
) (I)
В
соответствии со сделанным замечанием,
 = (0, x)
= (0, x)
f(t,
x, u) =

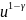 , t = 0, 1, … T-1
, t = 0, 1, … T-1
f(T,
x,
u)
=
 - эта функция от u
не зависит, и ее максимум, равный
- эта функция от u
не зависит, и ее максимум, равный
 совпадает с ней самой,
совпадает с ней самой,
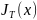 =
(II),
и любое
=
(II),
и любое
 = (0, x)
– оптимальное.
= (0, x)
– оптимальное.
Из (6) получаем
 =
=
 +
+
 (x-u))]
(III)
(x-u))]
(III)
При s = T-1
 =
=
 +
+

 ]
(IV),
]
(IV),
так как
 (x-u))
=
(x-u))
=

Для
 обозначим
обозначим
g(u)
=
+

Тогда
g’(u)
= (1-γ)
 + (1-γ)(-1)
+ (1-γ)(-1)
g’(u) =0 = (-1)
=
 =
1 +
=
1 +
 =
= (V)
(V)
u
=

так как g’(u) = (1-γ)(-γ) + (1-γ)(-γ) , < 0,
поэтому
 максимизирует g(u)
максимизирует g(u)
g
(
)
=
 + β A
+ β A
 =
=
=
+
 =
(1 + β A
=
(1 + β A
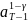 (
-1))
=
(
-1))
=
β
A
=

=
![]() (1 +
(1 + ![]() -1)
=
-1)
= ![]() (VI)
(VI)
Тогда ввиду (IV), (VI) (в (VI) вычитаем max y(u), подставляем в (IV))
![]() (x)
=
(x)
=![]()
Отметим,
что ![]() имеет тот же вид, что и
имеет тот же вид, что и ![]()
Для s= T-2
![]() (x)
=
(x)
=![]()
По
аналогии со сделанным выше находим, что
максимум достигается при ![]() = u
=
= u
= ![]() , где
, где ![]() = 1+
= 1+ ![]() и где
(x)
=
и где
(x)
= ![]()
Продолжая аналогично, находим для любого t
![]() (x)
=
(x)
= ![]() , где
, где ![]() = A,
а для
при t<T
имеем
= A,
а для
при t<T
имеем
![]() = 1+
= 1+ ![]() = 1 +
= 1 + ![]()
Оптимальное управление:
![]() (x)
=
(x)
= ![]() , t<T
, t<T
Для
нахождения оптимальных ![]() подставляем эти значения в рекурсивное
уравнение
подставляем эти значения в рекурсивное
уравнение
![]()
Предположим что для всех t тогда
![]()
![]()
![]() линейное
уравнение первого порядка с постоянным
коэффициентом
линейное
уравнение первого порядка с постоянным
коэффициентом
![]()
![]()
![]() =
=![]()
См
раздел 14 страница 1 ![]()
![]()
![]()
![]()
![]()

