Вариант 8.

1. Инвестиционный портфель: понятие, цели, виды.

2. Элементы и фазы инвестиционного проекта.

3. Номинальная стоимость облигации 1000 рублей. Срок обращения – два года, процентные платежи осуществляются один раз в год, купонная ставка 15 %. Рассчитайте максимально возможную рыночную цену облигации, если до погашения осталось два года. Доходность подобных облигаций обычно равна 20%.

Вариант 9.

1. Динамические показатели оценки эффективности инвестиционных проектов и методика их расчета

2. Оценка эффективности инвестирования в облигации.

3. Определите текущую цену обыкновенных акций, если размер дивидендных выплат по одной обыкновенной акции компании АВС составляет 10 денежных единиц, а уровень дивидендов 25 процентов.

Вариант 10.

1. Денежные потоки инвестиционного проекта и методика расчета денежного потока от операционной деятельности.

2. Иностранные инвестиции: понятие, роль, формы.

3. Инвестор, располагая денежными средствами в объеме 1 млн. рублей, решает 40% от общей суммы потратить на приобретение 400 акции, а оставшиеся 60% вложить в облигации. Облигации продавались с купоном 7% годовых. Курс акций вырос за год на 14%, дивиденд выплачивается раз в квартал в размере 120 рублей на одну акцию. Определить годовую доходность инвестиционной операции, налогообложение не учитывать.

Методические рекомендации по решению задач контрольной работы

(рассматривается каждый вариант).

Вариант 1

Доходность – относительный показатель, характеризующий эффективность инвестиционных операций и показывающий соотношение между инвестиционным доходом и инвестиционными затратами.

Инвестиционный доход от инвестиций в ценные бумаги складывается из двух составляющих:

1. Процентные выплаты в форме дивидендов при инвестировании в акции или купонных процентов при инвестировании в облигации.

2. Курсовая разница. Курс – рыночная цена ценной бумаги. Курсовая разница – это разница между ценой продажи акции или облигации и ценой покупки соответствующей ценной бумаги.

Инвестиционные затраты всегда связаны с покупкой ценных бумаг (акций, облигаций).

,

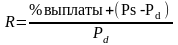где R – доходность ценной бумаги.

Ps – цена продажи ценной бумаги;

Pd – цена покупки ценной бумаги.

Следовательно, доходность портфеля акций можно определить по одному из двух вариантов:

1. Определив доход от продажи каждого вида акций, суммировав его, мы получим доход всего портфеля акций. Аналогично определяем затраты от покупки каждого вида акций, суммировав которые, получаем затраты портфеля. Доходность портфеля акций равна частному от деления дохода на затраты, которое для процентного выражения умножаем на 100.

2. Определяем доходность портфеля как средневзвешенную доходность различных акций. Для этого определяем доходность каждого вида акций, рассчитываем средневзвешенную, весами которой берём долю каждого вида акций в стоимости портфеля.

Rпортфеля = ∑ R_i х q_i ,

где R_i – доходность i ценной бумаги;

q_{i --} доля i ценной бумаги в стоимости портфеля.

Вариант 2

Полная доходность – это доходность за период владения акциями. Если акции находятся у инвестора меньше года, то полная доходность акций рассчитывается по следующей формуле:

,

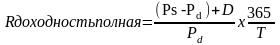где R – доходность акций из расчёта годовых;

P_d – цена покупки акций;

P_s – цена продажи акций;

D – дивиденды, полученные за период владения акциями;

T – период владения акциями в днях, если инвестор владел акциями меньше года.

Вариант 3

Метод чистой текущей стоимости (Net Present Value - NPV) оценки эффективности инве­стиционных проектов основан на определении чистой текущей сто­имости, на которую может увеличиться ценность (стоимость) фирмы в результате реализации проекта.

Чистая текущая стоимость (чистая приведенная стоимость, чис­тый дисконтированный доход) – это стоимость, полученная путем дисконтирования отдельно на каждый временной период разности всех оттоков и притоков доходов и расходов, накапливающихся за весь пери­од функционирования объекта инвестирования при фиксированной, заранее определенной процентной ставке.

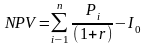
где Рi – годовые денежные потоки, генерируемые первоначальной инве­стицией в течение п лет;

r – норма дисконта;

I₀ – размер инвестированного капитала.

Метод оценки эффективности инвестиционных проектов по их чис­той текущей стоимости построен на предположении, что представля­ется возможным определить приемлемую ставку дисконтирования для определения текущей стоимости эквивалентов будущих доходов. Если чистая текущая стоимость положительна, проект можно принимать к осуществлению, поскольку проект в течение срока жизни возместит первоначальные затраты и обеспечит получение дохода. Отрицатель­ная величина NPV показывает, что желаемая норма дохода не обеспе­чивается и проект убыточен; его, как правило, отклоняют. При NPV = 0 проект только окупает произведенные затраты, но не приносит дохо­да. Из нескольких альтернативных проектов следует принимать про­ект с большим значением NPV.

Таким образом, критерием абсолютной эффективности инвести­ционного проекта является выполнение условия NPV_{проекта} > 0; критерием относительной эффективности альтернативных проектов является выполнение условия NPV_{проекта1} >NPV_{проекта2}

Пример. Изучаетcя предложение о вложении средств в четырехлет­ний инвестиционный проект, в котором предполагается получить доход за первый год – 20 тыс. ден. ед., за второй – 25 тыс. ден. ед., за третий – 30 тыс. ден. ед. Поступления доходов происходят в конце соответству­ющего года. Первоначальные инвестиции составляют 50 тыс. ден. ед. Средства для финансирования проекта будут получены в виде банков­ского кредита под 15% годовых. Выгодно ли участвовать в таком проекте?

Положительное значение NPV показывает, что чистые денежные пото­ки проекта покроют первоначальные затраты (а также выплаченные бан­ку процентные платежи) и принесут доход в размере 6 тыс. ден. ед. При таких условиях проект можно принять.

Уровень нормы дисконта выбирается инвестором в зависимости от его представлений об альтернативных возможностях вложений, кото­рые дает ему рынок капиталов и развитие собственного дела. Если чистая теку­щая стоимость проекта положительна, то это означает, что задействован­ный в проекте капитал имеет доходность более высокую, чем альтерна­тивные вложения по ставке г, и наоборот. Иногда в качестве расчетного процента можно использовать удовлетворяющий инвестора уровень годо­вой доходности вложений вне зависимости от существования более выгод­ных возможностей вложений. Особенно это имеет место при рассмотре­нии вопросов развития существующего направления деятельности.

Вариант 4

Капитал, необходимый фирме для финансирования реальным инвестиций, может быть получен разными путями. Привлечение инвестиционных ресурсов из любого источника финансирования связано с определенными затратами (выплатой дивидендов по акциям, про­центов по облигационным и банковским займам и др.), которые представляют собой цену капитала, направленного на финансирования инвестиций.

Общая сумма средств, которую нужно уплачивать за использование определенного объема финансовых ресурсов, выраженная в процентах к этому объему, называется ценой капитала (cost of capital).

Этот показатель отражает сложившийся на данном предприятии минимум возврата на вложенный в его деятельность капитал, а также характеризует ту норму рентабельности инвестированного капитала, которую должно обеспечивать предприятие, чтобы не уменьшить свою рыночную стоимость.

Поскольку обычно средства для инвестирования поступают из нескольких источников, ни один из которых нельзя определить кон­кретно как средство инвестирования данного исследуемого проекта, то стоимость капитала формируется под влиянием необходимости обеспечивать некий усредненный уровень прибыльности.

Поэтому средневзвешенная стоимость капитала (weighted average cost of capital – WACC) может быть определена как тот уровень доход­ности, который должна приносить инвестиционная деятельность, что­бы можно было обеспечить получение всеми категориями инвесторов дохода, аналогичного тому, что они могли бы получить от альтерна­тивных вложений с тем же уровнем риска.

Поскольку цена каждого источника средств различна, цена капи­тала предприятия рассчитывается по формуле средней арифметиче­ской взвешенной. Весами является доля каждого из источников средств в общей их сумме:

ССК = ∑ Рi х q_i

где ССК – цена всего авансированного капитала фирмы – средневзвешен­ная стоимость капитала, %;

Рi – цена i-го источника средств;

q_i – удельный вес i-го источника средств в общей их сумме.

Требуемый уровень доходности для акционеров, для инвестора, который желает получить капитал для своего инвестиционного проекта счёт эмиссии акций является уровнем его затрат, иными словами ценой капитала. Ставка банковского кредита – ценой банковского займа.

Цена источника капитала и доля источника капитала переводятся из процентного выражения в коэффициенты и подставляются в рассмотренную нами формулу.

Вариант 5

Цена банковского кредита. Во всех случаях специфическая стоимость долговых обязательств – это издержки на выполнение обя­зательств по выплате процентов. В общем случае цена любого источ­ника заемных средств – это ставка процента, которую предприятие вынуждено платить ссудодателю.

В случае банковского кредита эта ставка требует внесения двух уточнений. Во-первых, если для получения займа в соответствии с условиями кредитного соглашения нужны еще какие-то затраты (например, получение гарантии, оформление залога, страхования кре­дита за счет заемщика), то их размер следует учесть в цене капитала. При этом цена капитала увеличивается.

Второе уточнение касается учета противоналогового эффекта кре­дита. В большинстве стран налоговое законодательство разрешает на величину затрат, связанных с выплатой процентов, уменьшать налогооблагаемую прибыль. Это позволяет экономить отчисления по налогу на прибыль и сохраняет некоторый денежный поток. Поэтому реальная цена единицы такого источника средств меньше, чем уплачиваемый банку процент.

Стоимость заемного капитала с учетом этих уточнений можно определить по формуле

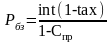
где Р_бз – цена банковского займа;

int – ставка процента (по кредитному договору);

tax – ставка налога на прибыль;

С_пр – уровень расходов по привлечению банковского кредита, выраженный в долях от его суммы.

Все данные для исчисления по формуле переводятся из процентов в коэффициенты. Ставка налога на прибыль – 20%.

Вариант 6

Общий подход к определению теоретической стоимости любой ценной бумаги заключается в следующем: чтобы определить, сколько, по мнению данного инвестора, должна стоить ценная бумага в данный момент времени, необходимо дисконтировать все доходы, которые он рассчитывает получить за время владения ценной бумагой, в том числе и доход от погашения облигации.

В зависимости от способа выплаты процентного дохода можно выделить два типа облигаций: (а) облигации с периодической выплатой процентного дохода или купонные облигации и (б) бескупонные (или дисконтные) облигации, доход по которым образуется за счет разницы между ценой погашения облигации и эмиссионной ценой и выплачивается при погашении облигации.

Рассмотрим облигацию с периодической выплатой процентного дохода.

Пример 1

Продается облигация номиналом 1000 руб. Процентная (купонная) ставка составляет 15% годовых. Выплата процентов производится один раз в год. До погашения облигации остается ровно 5 лет. Требуемая норма прибыли (доходность) на инвестиции с учетом риска, соответствующего данному типу облигаций, составляет 20%. Определить теоретическую цену облигации, которая должна быть равна приведенной стоимости всех предстоящих доходов облигации.

Решение

В конце каждого года держатель облигации получит процентный доход в размере 150 руб., а в конце пятого года – еще и сумму, равную номиналу облигации, т. е. 1000 руб. Определим дисконтированные (приведенные) стоимости доходов для каждого года и найдем их сумму.

Приведенная стоимость платежей составит (формула дисконтирования дана в третьем варианте):

^{первый год}

^{второй год}

^{третий год}

^{четвертый год}

^{пятый год}

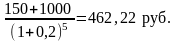
Таким образом, теоретическая цена облигации будет равна:

125 +104,17+86,80+72,34+462,22=850,47

Формула для определения теоретической стоимости облигации может быть представлена в виде:

где Р – теоретическая цена облигации;

D – процентный (купонный) доход в денежных единицах;

R – требуемая норма прибыли (ставка дисконтирования);

N – номинальная стоимость облигации; n – количество лет до погашения.

Если теоретическая цена (приведенная стоимость доходов от ценной бумаги) больше рыночной цены облигации, то облигацию следует купить, если цена облигации на рынке ценных бумаг больше, чем теоретическая стоимость, то облигацию покупать не следует.

Вариант 7

Полная доходность акции за несколько лет владения, определяется в том случае, если акция находилась у инвестора в течение несколько лет. Формула, по которой мы рассчитывали доходность для решения задачи второго варианта, дает искаженные результаты, так как здесь не учитывается стоимость денег во времени. Поэтому необходим другой подход.

Пример

Инвестор приобрел акцию за 50 руб. и продал её через четыре года за 84 руб. За время владения акцией инвестор получил дивиденды за первый год 3 руб., за второй год – 4 руб., за третий год – 4 руб. и за четвертый год – 5 руб. Определить доходность от операции с акцией.

Если не учитывать доходов от реинвестирования дивидендов, то после продажи акции инвестор имел на руках сумму 100 руб. (3  4  4  5  84). Таким образом, доходность за период владения акцией может быть определена по формуле:

где R – доходность акции;

P_s – цена продажи акции;

D – дивиденды за период владения акцией;

P_b – цена покупки акции,

n – количество периодов начисления дохода.

Используя эту формулу, получаем:

Вариант 8

Покупая ценную бумагу, инвестор приобретает, прежде всего, доход, который ценная бумага ему принесёт в будущем времени.

Поэтому максимально возможная цена ценной бумаги, в нашем варианте облигации, будет равна приведенной стоимости дохода от облигации за весь период владения ею инвестором, в том числе и от погашения облигации.

Формула для определения максимальной теоретической стоимости облигации может быть представлена в виде:

где Р – теоретическая цена облигации;

D – процентный (купонный) доход в денежных единицах;

R– требуемая норма прибыли (ставка дисконтирования);

N – номинальная стоимость облигации;

n – количество лет до погашения.

В условие задачи необходимо добавить, что инвестор рассчитывает на доходность, равную 10%.

Вариант 9

Уровень выплаты дивидендов характеризует соотношение сум­мы дивиденда и цены акции:

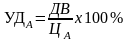
где УДа – уровень дивидендной отдачи акции, %;

ДВ – сумма дивиденда, выплаченная по акциям в рассматриваемом периоде;

Ц_А – рыночная цена акции на начало рассматриваемого периода.

Соответственно: Ц_А= ( ДВ : УД_А) х 100. Для удобства расчетов уровень дивидендов переводим в коэффициенты, а затем результат превращаем в проценты, умножив полученную относительную величину на 100.

Вариант 10

Доходность инвестиционной операции с ценными бумагами является относительной величиной, выраженной в процентах или коэффициентах. Доходность – это соотношение дохода и затрат инвестора. Сумма затрат – это затраченные на приобретение ценных бумаг денежные средства. Доход состоит из двух составляющих: 1 – доход в форме % выплат; 2 – доход от продажи ценных бумаг в форме курсовой разницы (см. рекомендации для 1-ого варианта.)

Возможен и один вариант дохода: Например, инвестор не собирается продавать ценную бумагу, то есть остается доход только в форме процентных выплат или ценная бумага не предусматривает процентные выплаты, в этом случае остаётся доход только от продажи или погашения (доход от бескупонных облигаций).

доход

Доходность = --------------- х 100

затраты

Пример:

Акция приобретена инвестором за 400 ден ед., продана ровно через год. Курс акции за год упал на 2%. Дивиденды в размере 40 ден. ед. на акцию были выплачены. Определить доходность за период владения акцией.

R = [400 х (1 – 0,02) – 400 + 40] : 400 = 0,08, то есть 8 %