Контрольная работа 2 / 2-10_Высшая математика / Контрольная работа по высшей математике№2

Контрольная работа по высшей математике №2

1. В прямоугольном треугольнике даны: вершина острого угла и уравнение одного из катетов. Записать общее уравнение другого катета.

Решение:

Так как прямая AB перпендикулярна прямой , то направляющий вектор прямой AB равен нормальному вектору прямой , т.е. , тогда каноническое уравнение катета AB имеет вид

- общее уравнение катета AB.

2. Высота проведенная из вершины треугольника АВС, пересекает прямую ВС в точке . - уравнение высоты, опущенной из вершины В. Определить координаты вершины С.

Решение:

Так как прямая - высота, то прямая перпендикулярна прямой АС. Отсюда следует что направляющий вектор прямой АС равен нормальному вектору прямой , т.е. , тогда каноническое уравнение прямой АС имеет вид: - общее уравнение АС.

по условию

имеем

тогда

- общее уравнение прямой DC.

Найдем координаты точки С из пересечения прямых AC и DC:

тогда

Ответ:

3. Записать общее уравнение плоскости, которая проходит через точку и ось OY.

Решение:

Возьмем на оси OY какие-нибудь две точки и

Тогда искомое уравнение плоскости, т.е. плоскости проходящей через точки имеет вид:

- общее уравнение искомой плоскости.

4. Найти значение параметра m в уравнении прямой , если известно, что эта прямая параллельна плоскости .

Решение:

Найдем направляющий вектор прямой

В качестве направляющего вектора можно взять

т.к. заданная прямая параллельна плоскости , то направляющий вектор прямой перпендикулярен нормальному вектору плоскости , который равен отсюда

Ответ:

5. Найти длину отрезка, отсекаемого от оси аппликат плоскостью, проходящей через точки и пересекающей оси ординат и абсцисс в точках .

Решение:

Составим уравнение плоскости проходящей через точки

по условию эта плоскость проходит через точку

отсюда искомое уравнение плоскости имеет вид:

Найдем пересечение полученной плоскости с осью OZ:

Ответ: длина отрезка отсекаемого от оси аппликат заданной плоскостью равна 6.

6. Найти координаты точки пересечения прямой с плоскостью, содержащей прямые , .

Решение: найдем уравнение плоскости содержащей прямые и .

прямая проходит через точку , тогда искомое уравнение плоскости есть уравнение плоскости проходящей через точки K, M, N

- искомое уравнение плоскости.

Найдем координаты точки пересечения прямой с полученной плоскостью:

из уравнения (1): подставим в (2):

тогда

Ответ: координаты точки пересечения равны

7. Найти радиус сферы с центром в точке , если она касается плоскости

Решение: Радиус сферы с центром в точке С равен расстоянию от точки С до плоскости

. Из уравнения плоскости имеем:.

Координаты точки С: , получим:

Ответ: R=5

8. Дана кривая .

1. Доказать, что эта кривая – эллипс.

2. Найти координаты его симметрии.

3. Найти его большую и малую полуоси.

4. Записать уравнение фокальной оси.

5. Построить данную кривую.

Решение: преобразуем данное уравнение, выделив полные квадраты:

введем новые переменные: , тогда - эллипс.

Центр симметрии находится в точке , большая полуось а=3, малая полуось b=2.

Уравнение фокальной оси

9. Дана кривая .

1. Доказать, что данная кривая парабола.

2. Найти координаты ее вершины.

3. Найти значение ее параметра р.

4. Записать уравнение ее оси симметрии.

5. Построить данную параболу.

Решение: преобразуем данное уравнение, выделив полный квадрат:

получаем: , получим: - каноническое уравнение параболы.

Вершина параболы находится в точке (-1;2), прямая у=2 – ось симметрии.

10. Дана кривая

1. Доказать, что эта кривая - гипербола.

2. Найти координаты ее центра симметрии.

3. Найти действительную и мнимые полуоси.

4. Записать уравнение фокальной оси.

5. Построить данную гиперболу.

Решение: Приведем квадратичную форму: к главным осям. Матрица квадратичной формы имеет вид: . Записываем характеристическое уравнение этой матрицы:

собственные числа.

Так как , то заданная кривая – гипербола.

Найдем ортонормированный собственный вектор соответствующий собственному числу

- собственный вектор

тогда - ортонормированный собственный вектор.

Найдем ортонормированный собственный вектор соответствующий собственному числу

- собственный вектор

тогда - ортонормированный собственный вектор.

Запишем матрицу Q перехода от базиса О, i, j к

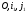
выражаем новые координаты и через старые:

Заданное уравнение в новой системе координат примет вид:

Перейдем к новой системе координат :

получим: - каноническое уравнение гиперболы.

Решая систему найдем координаты центра симметрии гиперболы , действительная полуось равна , мнимая полуось равна .

Построим гиперболу. Для этого сначала в старой системе координат построим новую систему координат. Новые оси направлены по прямым (ось ) и (ось ).

y

O₁

x₂

x

y₂

-1

-2