Томский межвузовский центр дистанционного образования Томский государственный университет систем управления и радиоэлектроники (ТУСУР)
Контрольная работа №2
по дисциплине “Высшая математика - 1”, Магазинников Л.И.
Вариант №2.8

Выполнил: студент ТМЦДО группы специальности

1. Даны координаты вершин треугольника A(1,3), B(2,8), C(6,7). Запишите общее уравнение его высоты AH.

Так как прямая AH перпендикулярна BC, то в качестве вектора нормали к прямой AH можно взять любой параллельный BC вектор. BC = (4, -1) || (-4, 1). В качестве вектора нормали прямой AH примем вектор (-4;1). Уравнение прямой AH можно записать в виде

-4x + y – (- 4·1 + 1·3) = 0;

-4x + y + 1 = 0

4x - y – 1 = 0

Ответ: Уравнение высоты треугольника ABC: 4x - y – 1 = 0.

2. В треугольнике ABC из вершины A проведены высота и медиана. Даны: вершина B(6, 5), уравнение высоты x + y = 2 и уравнение медианы 2x – 3y + 1 = 0. Найдите координаты вершины С.

_{Координаты вершины A можно найти как точку пересечения высоты AH и медианы AM, решая систему уравнений}

x = 1, y = 1, т.е. A (1,1).

Точка M имеет координаты . Точка C лежит на прямой BC, а M на медиане. Прямая BC перпендикулярна высоте, поэтому в качестве вектора нормали можно взять любой вектор, перпендикулярный к вектору (1, 1), например N (-1, 1). Уравнение BC можно записать в виде

-x + y – (-6 + 5) = 0

-x + y + 1 = 0

x – y –1 = 0

Для отыскания и имеем систему

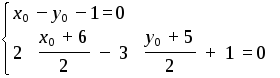
Решая систему, находим = 2, = 1.

Ответ. C (2, 1).

3. Запишите общее уравнение плоскости, проходящей через точки и 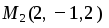перпендикулярно плоскости x + 4y – 5z + 3 = 0.

Решение: В качестве одного вектора, параллельного искомой плоскости воэьмём вектор .

Искомая плоскость также параллельна вектору нормали плоскости x + 4y – 5z + 3 = 0. Выражаем из уравнения плоскости этот вектор и принимаем его в качестве второго вектора: .

В качестве вектора нормали к искомой плоскости берём вектор N = [] = Разложим определитель по первой строке:

Т.е. N = ( 3, 3, 3). Записываем уравнение плоскости 3х + 3у + 3z + D = 0.

Для определения D используем условие, что плоскость проходит через точку

3·1 + 3·(-2) + 3·4 + D = 0

D = -9

Уравнение 3x + 3y + 3z – 9 =0 или

x + y + z – 3 = 0

является искомым.

Ответ: x + y + z – 3 = 0.

4. Найдите координаты проекции точки М( 3, –1, -3) на плоскость 2х + у – 4z + 4 = 0.

Решение: По заданию надо найти координаты точки . Прямая, соединяющая точку М с точкой является перпендикуляром к плоскости 2х + у – 4z + 4 = 0.

Из уравнения плоскости 2х + у – 4z + 4 = 0 видно, что вектором нормали этой плоскости является вектор l( 2, 1, -4). Данный вектор параллелен прямой , а следовательно является направляющим для данной прямой.

Выражаем уравнение прямой в координатной форме.

Находим то значение параметра t, при котором происходит пересечение прямой и плоскости. Так как точка ( 3 + 2t, -1 + t, -3 – 4t) лежит в данной плоскости, то её координаты удовлетворяют уравнению плоскости, следовательно,

2(3 + 2t) + (-1 + t) – 4(-3 – 4t) + 4 = 0

21t + 21 = 0

t = -1.

Полагая в параметрических уравнениях прямой t = -1, находим точку пересечения

( 1, -2, 1).

Ответ: ( 1, -2, 1).

5. Найдите коэффициент А в уравнении плоскости Ax + y + Cz + D = 0, проходящей через точки P( 1, 1, 8), O( 0, 0, 0) параллельно прямой .

Решение: Перепишем уравнение прямой в параметрическом виде:

Коэффициенты при параметре t в этих уравнениях определяют координаты направляющего вектора прямой. Итак, известны координаты вектора ( 1, -1, 6) , являющегося также направляющим вектором для плоскости(т.к. прямая параллельна плоскости по условию).

В качестве второго вектора, параллельного плоскости возьмём вектор OP( 1, 1, 8).

В качестве вектора нормали плоскости возьмём вектор N = [] =

Разложим определитель по первой строке:

Отсюда видно, что А = 7, С = -1.

Ответ: А = 7.

6) При каких значениях параметров а и с прямая

_{пересекает две другие прямые:}

и

Решение: Запишем параметрическое уравнение прямой, заданной общим уравнением.

Так как , то неизвестное z можно принять в качестве свободного и записать

_{Находим общее решение системы :}

Полагая z = t, записываем параметрическое уравнение прямой:

_{Аналогично записываем уравнение в параметрическом виде для другой прямой:}

Условие пересечения двух прямых:

Для первой прямой: = (3,3,0); = (1,1,-1); = (2,3,1); = (a,-1,c).

Для второй прямой: = (,,0); = (1,1,-1); = (,,1); = (a,-1,c).

Тогда

Ответ: a = 2; c =1.

7. Найдите радиус сферы, если известно, что она касается двух плоскостей: x – 2y + 2z + 22 = 0 и x – 2y + 2z + 10 = 0.

Решение: Векторами нормали для обеих плоскостей является вектор N( 1, -2, 2), следовательно плоскости параллельны, а значит расстояние d между ними является диаметром сферы.

Возьмём любую точку на первой плоскости, например M( -22, 0, 0). Она удалена от плоскости x – 2y + 2z + 10 = 0 на расстояние d. Поэтому

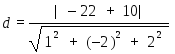
Находим радиус сферы:

_{Ответ: R = 2.}

7. Дана кривая .

8.1) Докажите, что эта кривая – эллипс.

Преобразуем данное уравнение, выделив полные квадраты:

Введём новые переменные .

Тогда:

Это уравнение определяет эллипс.

8.2) Найти координаты центра его симметрии.

Центр симметрии находится в точке ( 2; 8).

3. Найти его большую и малую полуоси.

Так как ,

то a = 2 – большая полуось.

b = 3 – малая полуось.

8.4) Записать уравнение фокальной оси.

x = 2 – фокальная ось.

8.5) Построить данную кривую:

7. Дана кривая .

9.1) Докажите, что данная кривая – парабола.

Введём новые переменные

_{Тогда уравнение примет вид}

Оно определяет параболу.

9.2) Найдите координаты ее вершины.

Вершина параболы О( 2; 5).

9.3) Найти значение ее параметра р.

Так как , то

В качестве х возьмём координаты вершины параболы:

p = .

9.4) Записать уравнение её оси симметрии.

Осью симметрии является прямая ( x – 2 = 0), т. е. х = 2.

9.5) Построить данную параболу

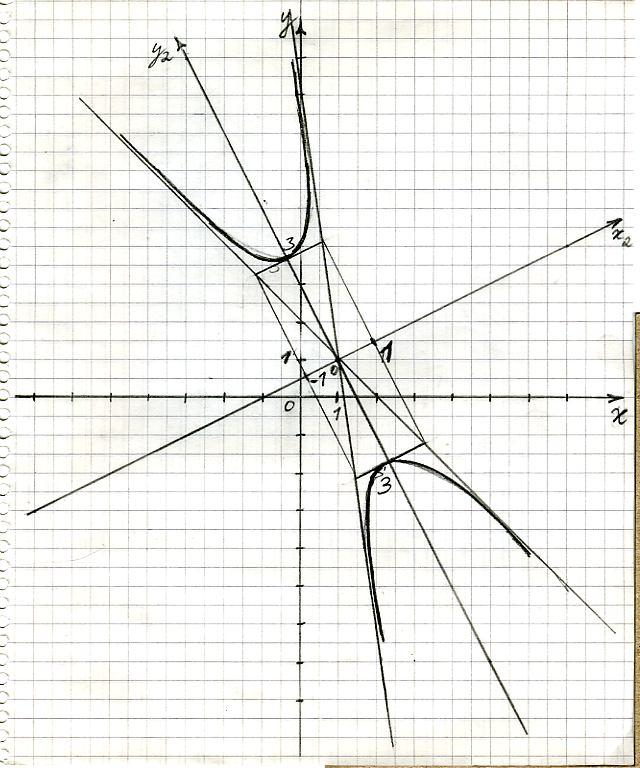
7. Дана кривая х² - 8ху + 7у² + 6х - 6у + 9 = 0.

10.1) Докажите, что эта кривая – гипербола.

Квадратичную форму В(х, у) = х² - 8ху + 7у² приводим к главным осям. Для этого записываем матрицу этой квадратичной формы

и находим ее собственные числа и векторы. Записываем и решаем характеристическое уравнение матрицы В.

т.к. собственные числа имеют разные знаки, то данное уравнение определяет кривую гиперболического типа. Находим собственные векторы матрицы В.

Для собственного числа получаем систему

Отсюда . Полагая, находим единичный собственный вектор .

Другой собственный вектор при : .

Базис (i₁; j₁) принят правым. Переходим от базиса (0; i; j) к (0₁; i₁; j₁). Запишем матрицу перехода:

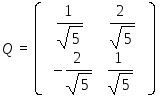и обратную к ней Q^-1 = Q^т =.

Новые координаты (х₁, у₁) связаны со старыми (х, у) соотношениями:

_или

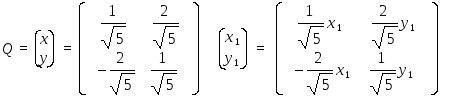
Получаем систему:

Получаем систему:

Уравнение данной кривой в новой системе координат:

Данное уравнение – есть уравнение гиперболы.

2. Найти координаты ее центра симметрии О₁(х, у)

Теперь

В системе координат (о₁; i₁; j₁) гипербола имеет уравнение:

Оси о₁х₂, о₁у₂ направлены по прямым x - 2y + 1 = 0 ; 2x + y - 3 = 0.

Координаты точки О₁, являющиеся центром симметрии гиперболы, находим решая систему:

Получаем х = 1; у = 1.

О₁(1; 1).

2. Найдите действительную и мнимую полуоси

а – действительная полуось.

b = – мнимая полуось.

10.4) Записать уравнение фокальной оси.

Фокальной осью является прямая х₂ = 0.

x - 2y + 1 = 0.

Асимптотами являются прямые .

5. Постройте данную гиперболу.