
Контрольная работа 2 / 2- 0_Высшая математика № 1
.doc
Томский межвузовский центр дистанционного образования
Томский государственный университет
систем управления и радиоэлектроники (ТУСУР)
Кафедра программного обеспечения вычислительной
техники и автоматизированных систем
Контрольная работа № 2
по дисциплине «Высшая математика № 1»
(Учебное пособие «Линейная алгебра и
аналитическая геометрия»,
автор Магазинников Л.И., Магазинникова А.Л., 2003г. )
Выполнил:
студент ТМЦДО
гр.: з-434-29а
специальности 220400
Ковалева Лилия Олеговна
15 июля 2004 г.
г. Норильск
2004г
Вариант 2.9
-
Даны координаты вершин треугольника
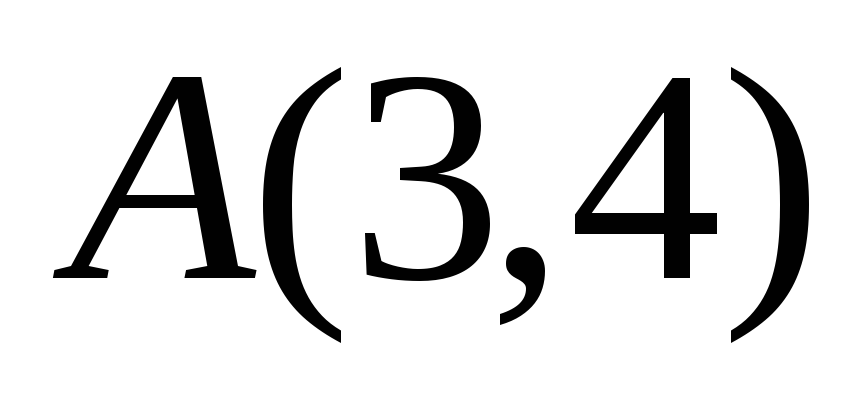 ,
,
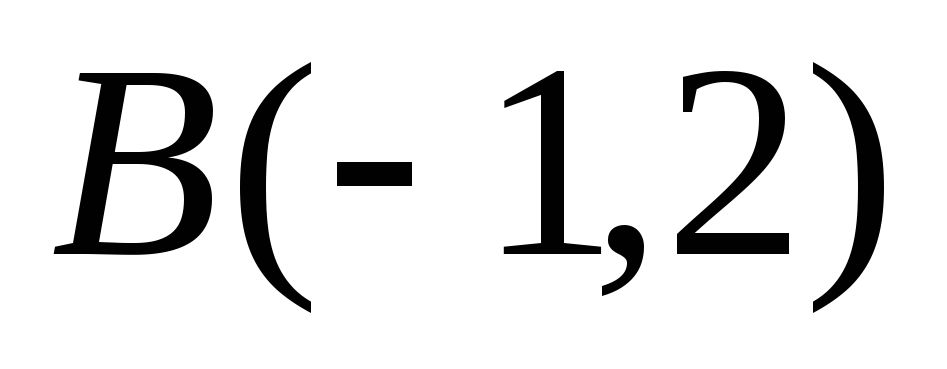 ,
,
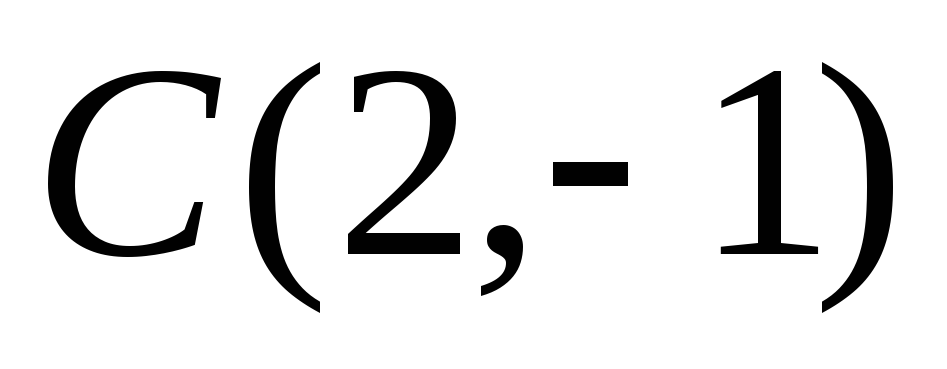 .
Запишите общее уравнение средней линии
треугольника, параллельной
.
Запишите общее уравнение средней линии
треугольника, параллельной
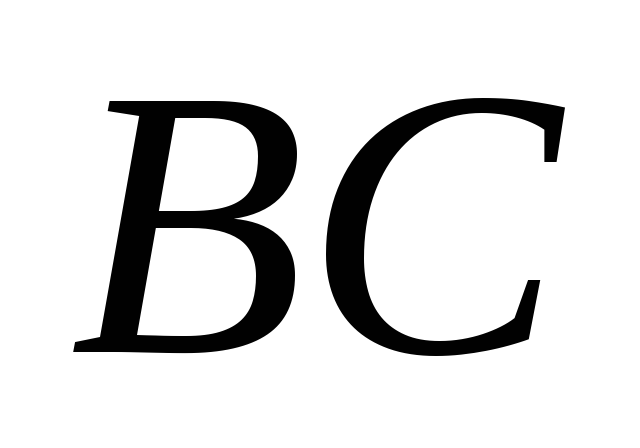 .
.
Р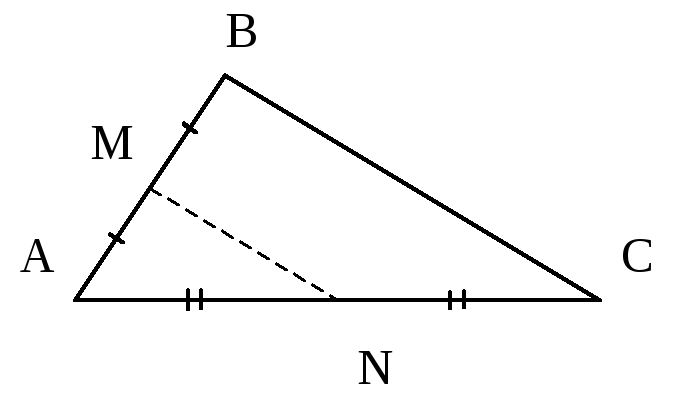 ешение:
Находим координаты точек средней
линии треугольника, параллельной
ешение:
Находим координаты точек средней
линии треугольника, параллельной
![]() .
.
![]() ,
,
![]() .
Уравнение прямой можно записать в виде
.
Уравнение прямой можно записать в виде
![]() ,
где
,
где
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
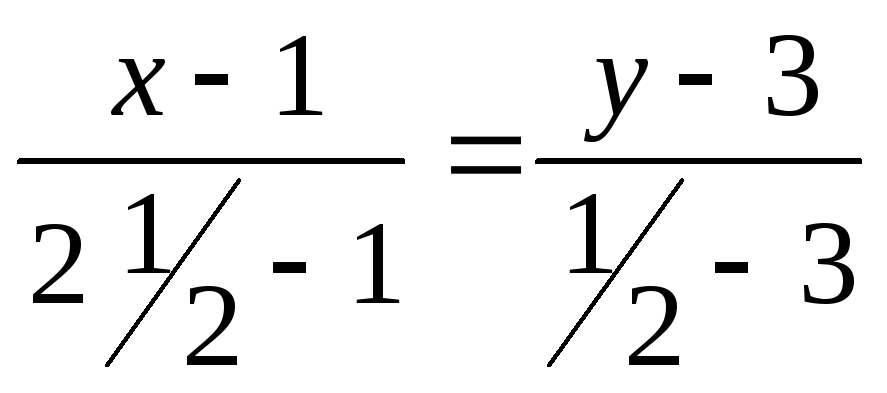 ,
,
![]()
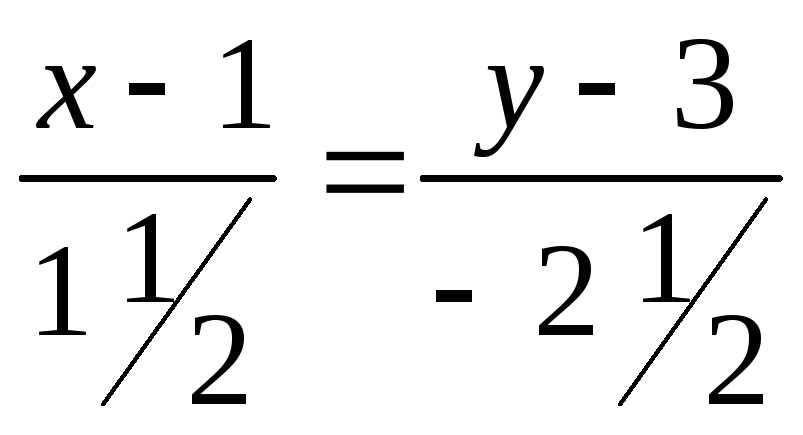 ,
,
![]() ,
,
![]() ,
,
![]() .
.
Ответ:
![]() .
.
-
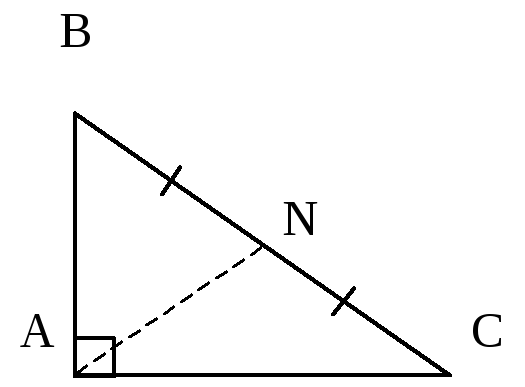
В прямоугольном треугольнике
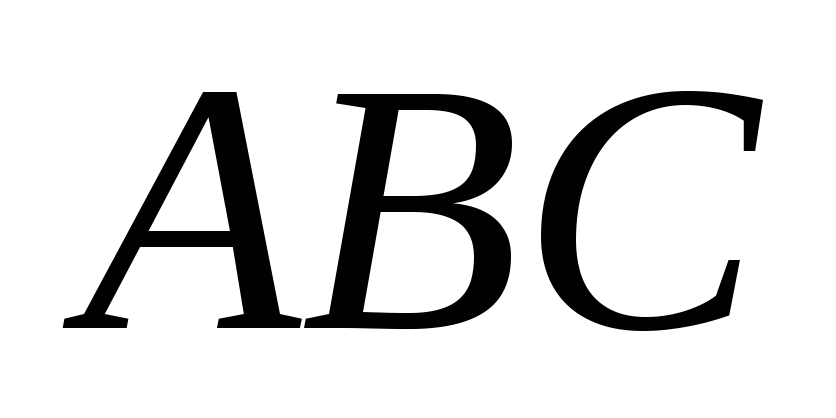 известны: уравнения медианы
известны: уравнения медианы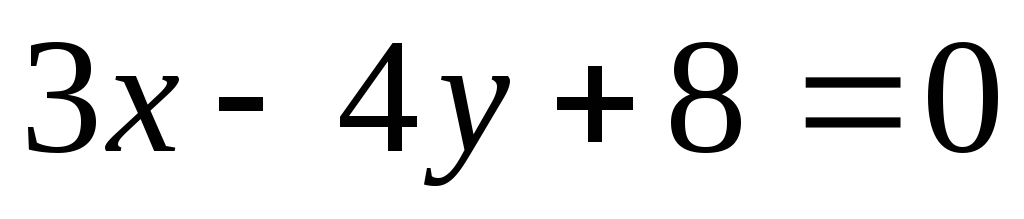 ,
проведенной из вершины
,
проведенной из вершины
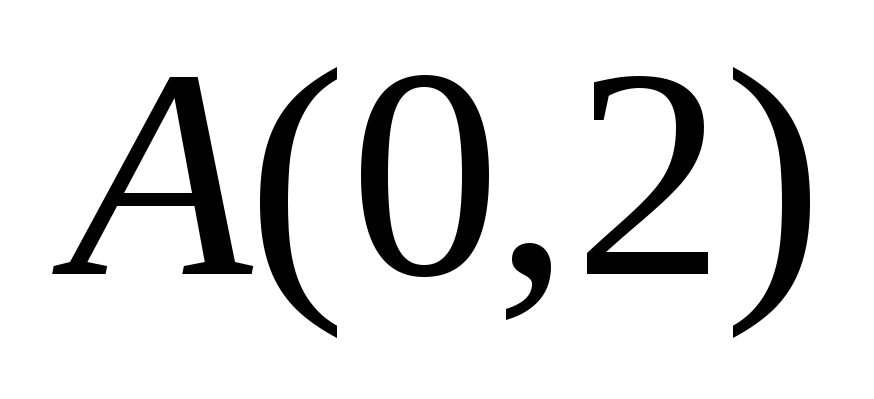 прямого
угла, и вершина
прямого
угла, и вершина
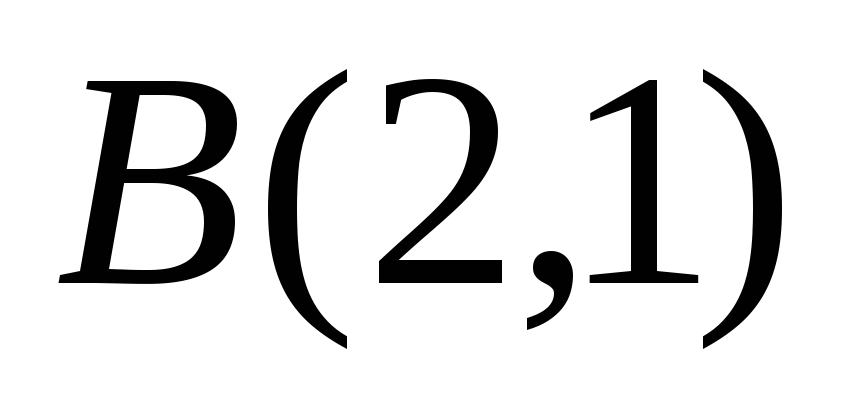 .
Найдите координаты
.
Найдите координаты
 вершины
вершины
 треугольника.
треугольника.
Р
![]() ,
как прямой проходящей через две точки
,
как прямой проходящей через две точки
![]() ;
;
![]() (уравнение с угловым коэффициентом)
(уравнение с угловым коэффициентом)
![]() .
Из условия перпендикулярности катетов
.
Из условия перпендикулярности катетов
![]() и
и
![]() ,
,
![]() ,
тогда
,
тогда
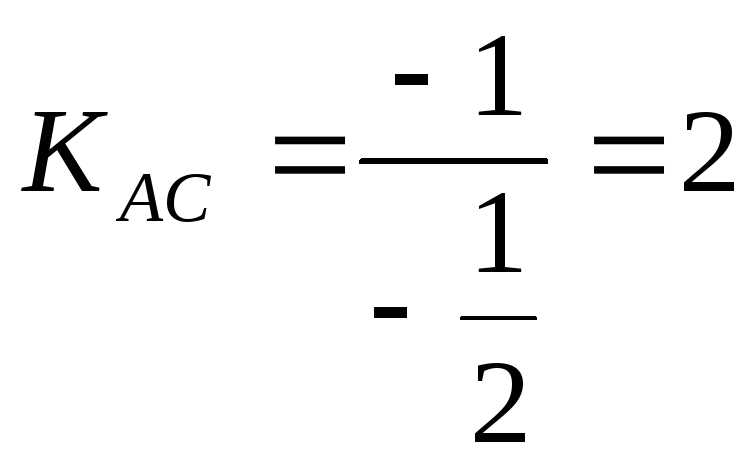 ,
уравнение
,
уравнение
![]() ,
проходящей через точку
,
проходящей через точку
![]() будет
будет
![]() ;
;
![]() или
или
![]() .
Пусть
.
Пусть
![]() ,
тогда
,
тогда
![]() .
Так как
.
Так как
![]() - медиана треугольника, проведенная к
стороне
- медиана треугольника, проведенная к
стороне
![]() ,
то
,
то
![]() - середина отрезка
- середина отрезка
![]() ,
координаты этой точки
,
координаты этой точки
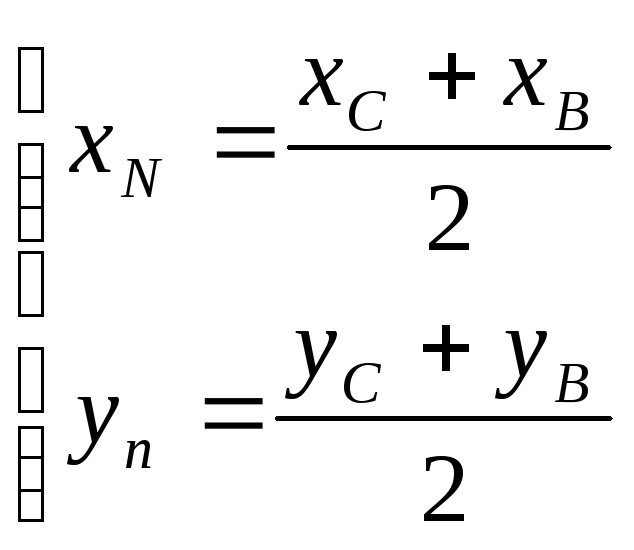 или
или
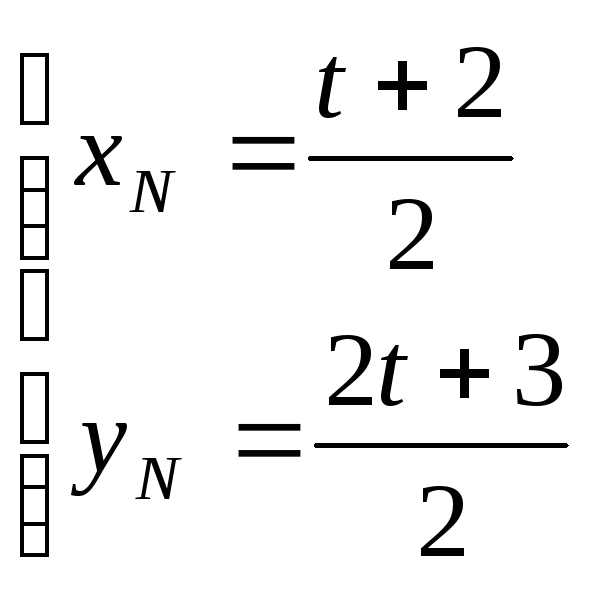 .
Точка
.
Точка
![]() принадлежит прямой
принадлежит прямой
![]() ,
тогда
,
тогда
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ,
тогда координаты вершины
,
тогда координаты вершины
![]() треугольника
треугольника
![]()
![]() ,
,
![]() ,
т.е.
,
т.е.
![]() .
.
Ответ:
![]()
-
Запишите общее уравнение плоскости, проходящей через точки
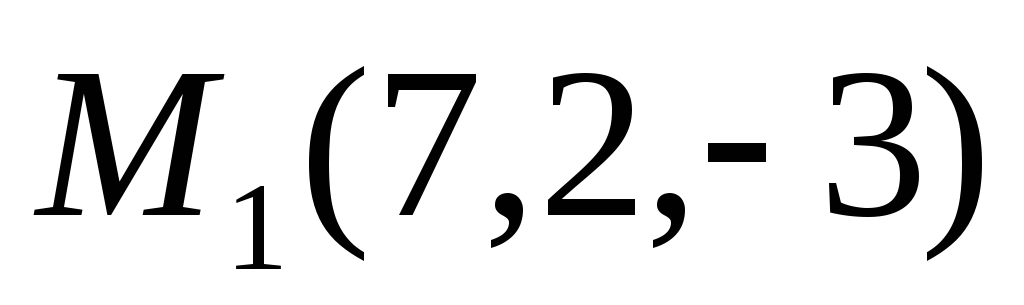 и
и
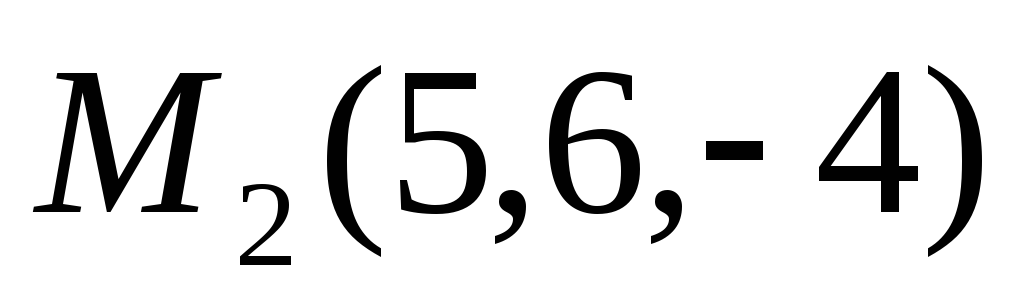 параллельно оси
параллельно оси
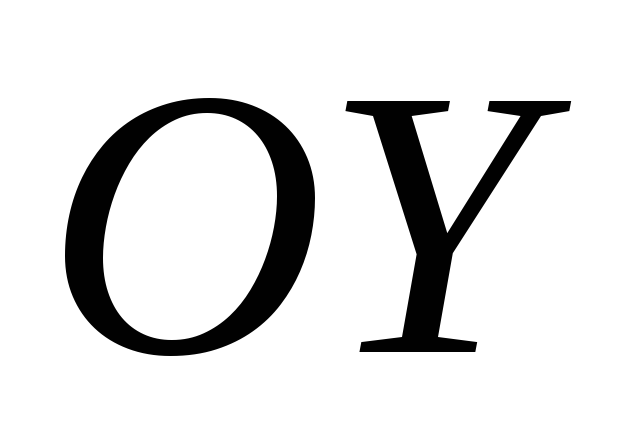 .
.
Решение: Данная плоскость параллельна
векторам
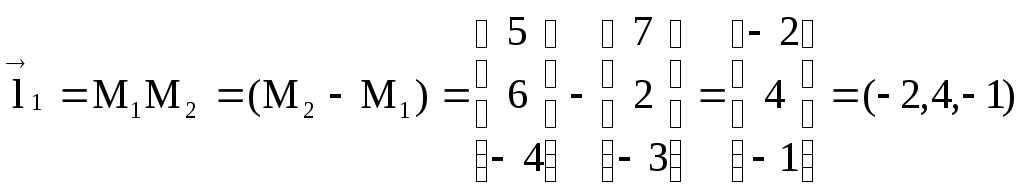 и
и
![]() ,
поэтому её вектор нормали
,
поэтому её вектор нормали
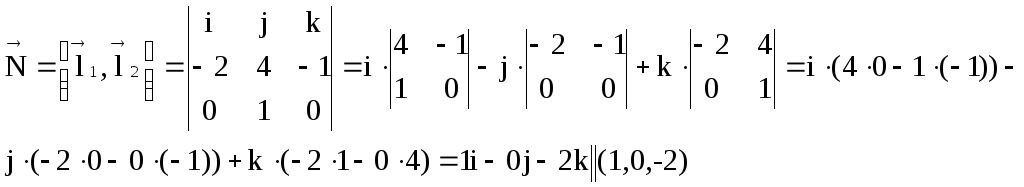 Записываем уравнение плоскости
Записываем уравнение плоскости
![]() ,
,
![]() .
Так как плоскость проходит через точку
.
Так как плоскость проходит через точку
![]() ,
то
,
то
![]() ,
,
![]() ,
,
![]() .
Искомое уравнение имеет вид
.
Искомое уравнение имеет вид
![]() .
.
Ответ:
![]()
-
Найдите коэффициент
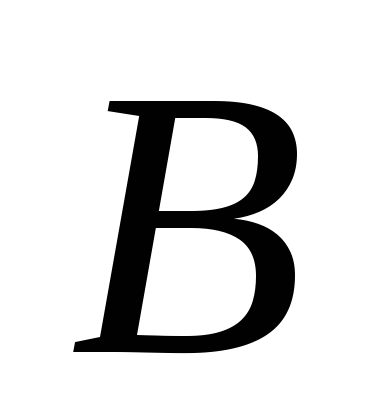 в уравнении плоскости
в уравнении плоскости
 ,
проходящей через точки
,
проходящей через точки
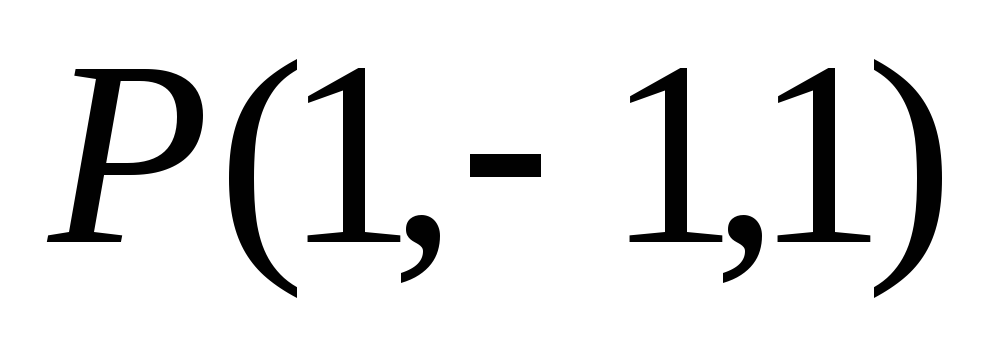 ,
,
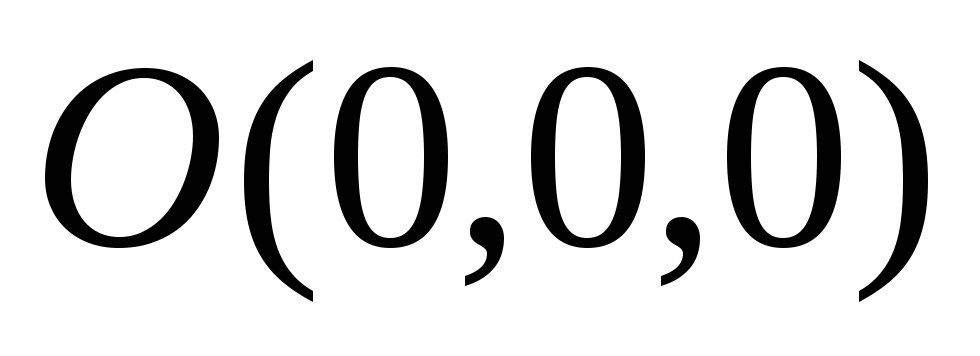 параллельно прямой
параллельно прямой
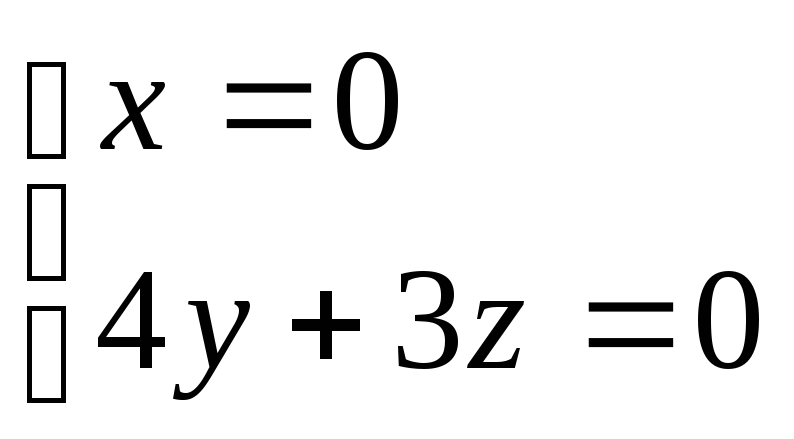 .
.
Решение: найдем канонические
уравнения заданной прямой
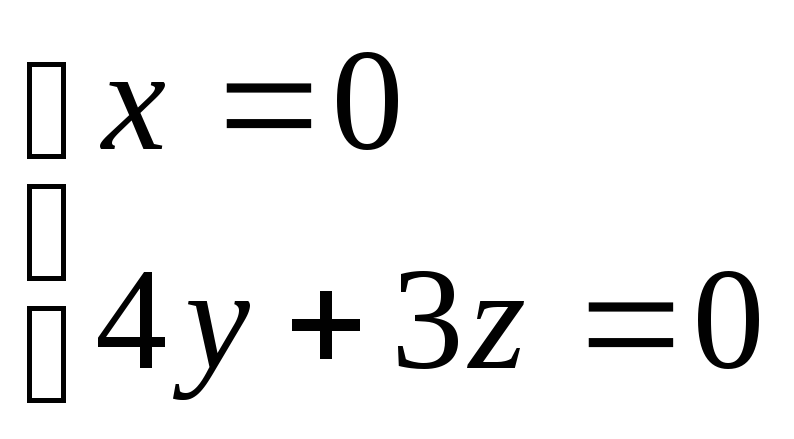
![]() .
Искомая плоскость параллельна
вектору
.
Искомая плоскость параллельна
вектору
![]() и направляющему вектору
и направляющему вектору
![]() прямой. Тогда уравнение плоскости можно
записать в виде (с учетом того, что она
проходит через
прямой. Тогда уравнение плоскости можно
записать в виде (с учетом того, что она
проходит через
![]() )
)
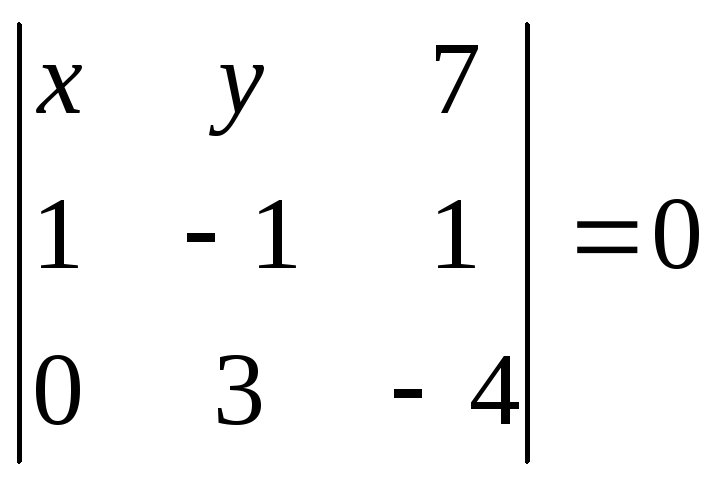 ,
или
,
или
![]() .
.
![]() ,
сравнивая полученное уравнение с
заданным
,
сравнивая полученное уравнение с
заданным
![]() видим, что
видим, что
![]() ,
,
![]() ,
,
![]() .
.
Ответ:
![]() .
.
-
При каких значениях параметров
 и
и
 прямая
прямая
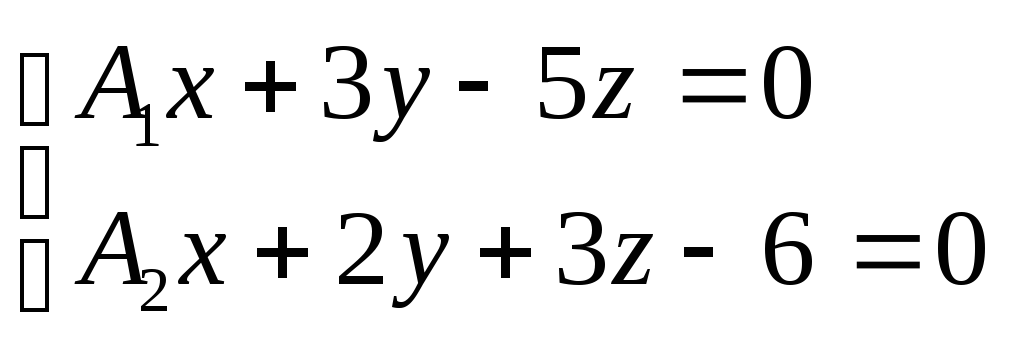 параллельная прямой
параллельная прямой
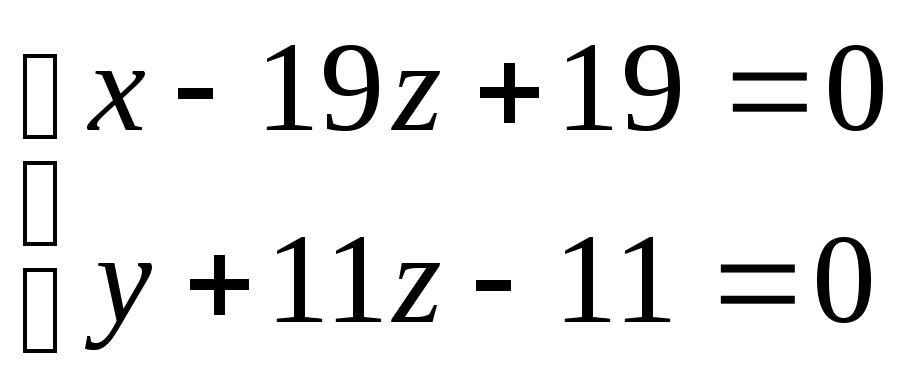 .
.
Решение: прямые в пространстве
параллельны, если параллельны и их
направляющие векторы. Найдем канонические
уравнения заданных прямых.
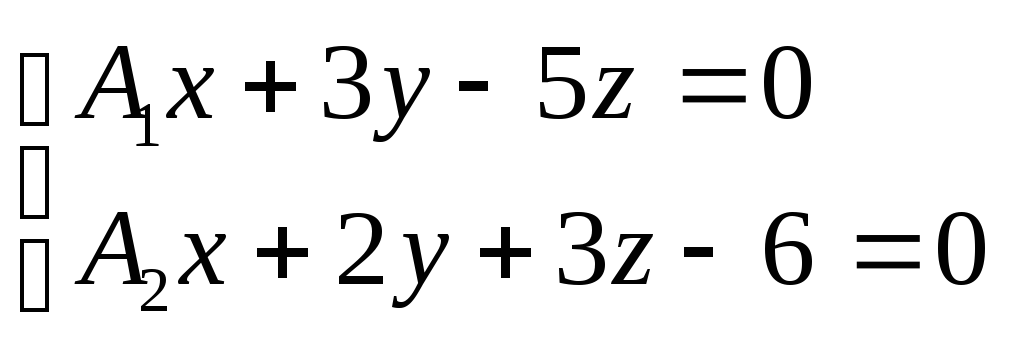 ,
пусть
,
пусть
![]() ,
тогда система примет вид
,
тогда система примет вид
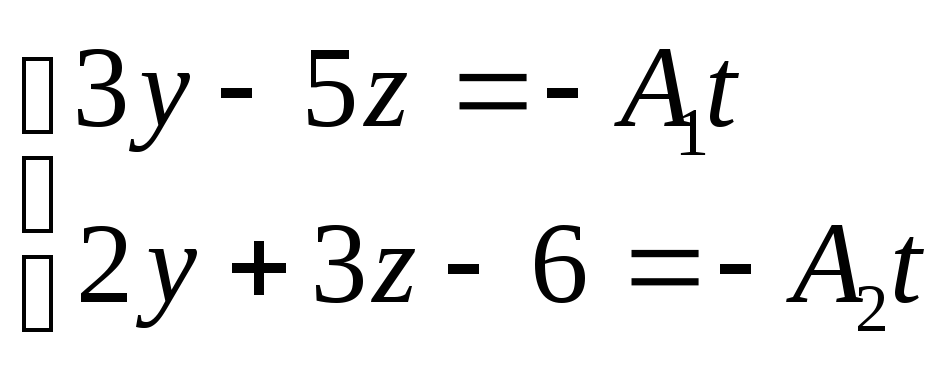 ,
вычитая из первого уравнения второе
получим
,
вычитая из первого уравнения второе
получим
![]() ,
это уравнение представляем в первом
,
это уравнение представляем в первом
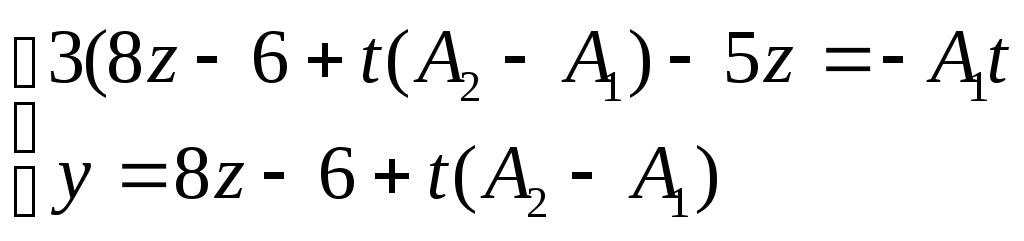 ;
;
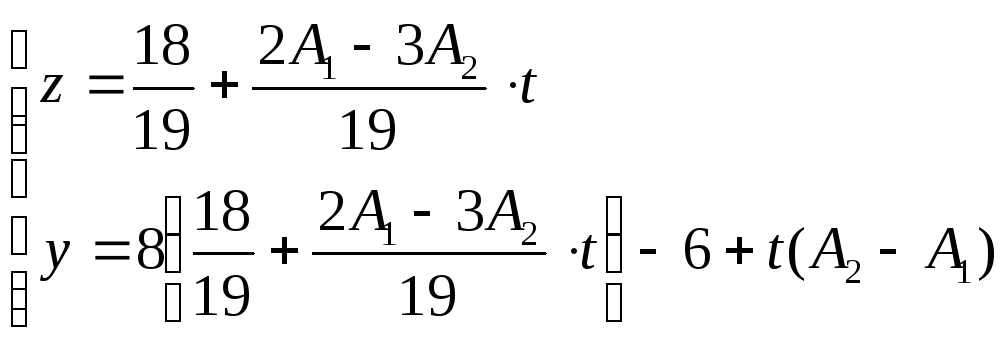 ;
;
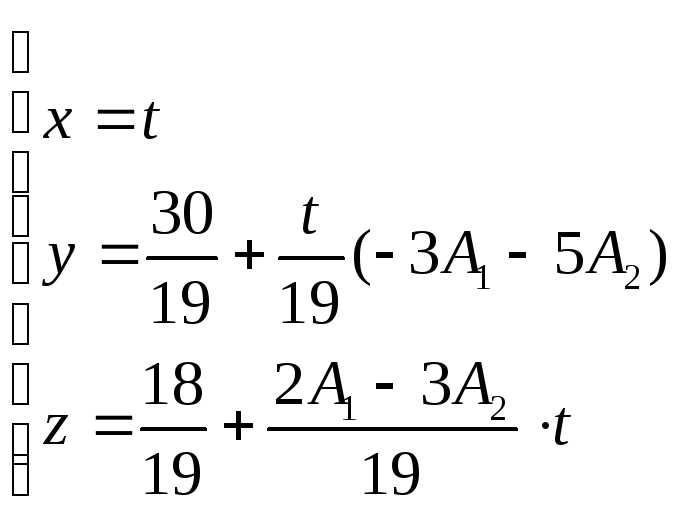 - параметрические уравнения прямой,
тогда канонические уравнения этой
прямой
- параметрические уравнения прямой,
тогда канонические уравнения этой
прямой
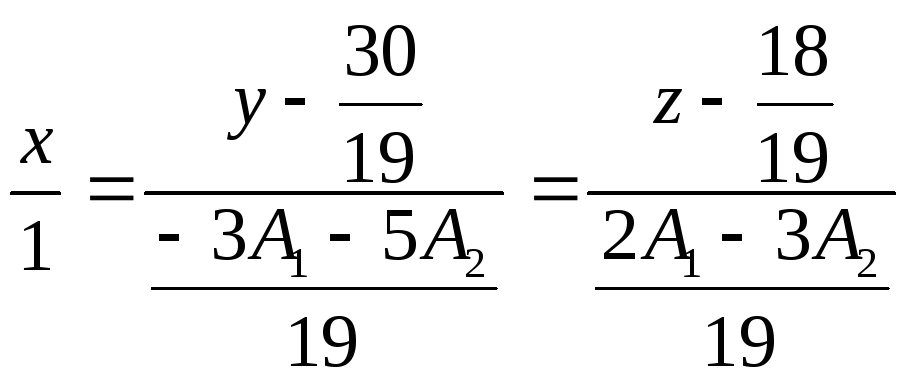 .
Направляющим вектором этой прямой
возьмем
.
Направляющим вектором этой прямой
возьмем
![]() .
Преобразуем к каноническому виду прямую
.
Преобразуем к каноническому виду прямую
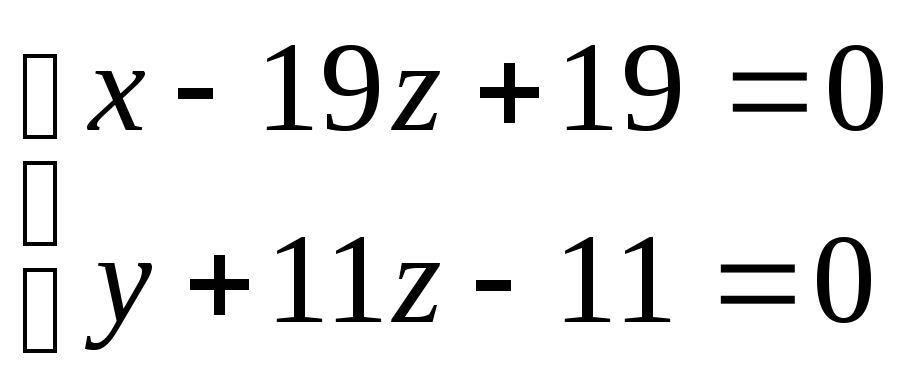 ,
пусть
,
пусть
![]() ,
тогда
,
тогда
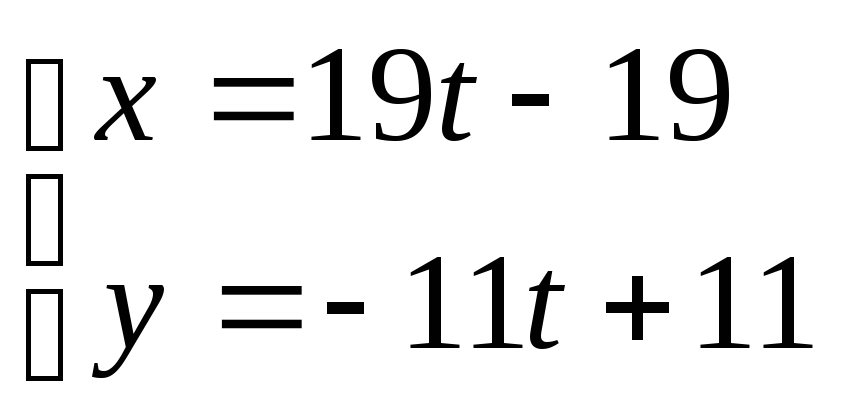 ;
;
![]() .
Направляющий вектор этой прямой
.
Направляющий вектор этой прямой
![]() .
Из условия следует, что
.
Из условия следует, что
![]() .
Тогда выполняется
.
Тогда выполняется
![]() ;
;
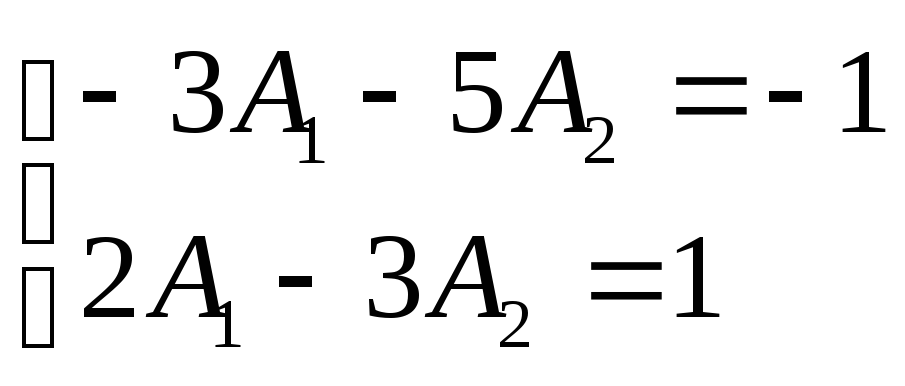 ,
решая последнюю систему получаем:
,
решая последнюю систему получаем:
![]() ,
,
![]() .
.
Ответ:
![]() ,
,
![]() .
.
-
Найдите длину отрезка, отсекаемого от оси аппликат, плоскостью, содержащей прямую
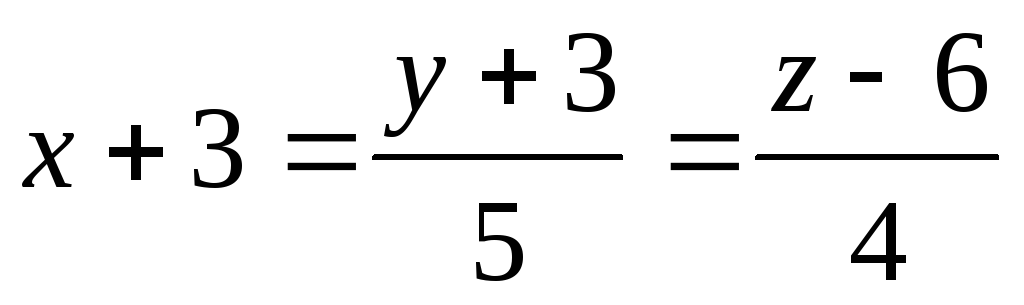 и отсекающей на осях абсцисс и ординат
одинаковой длины отрезки.
и отсекающей на осях абсцисс и ординат
одинаковой длины отрезки.
Р
![]() в
в
![]() ,
ось
,
ось
![]() в
в
![]() ,
ось
,
ось
![]() в
в
![]() ,
из условия
,
из условия
![]() .
Плоскость параллельна направляющему
вектору прямой
.
Плоскость параллельна направляющему
вектору прямой
![]() и вектору
и вектору
![]() или вектору
или вектору
![]() ,
,
![]() .
Поэтому вектор нормали плоскости
.
Поэтому вектор нормали плоскости
![]() .
.
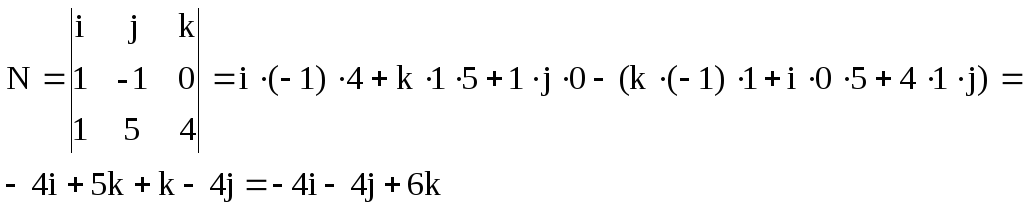 .
.
Возьмем
![]() ,
,
![]() ,
тогда уравнение плоскости вида
,
тогда уравнение плоскости вида
![]() ,
точка
,
точка
![]() из условия принадлежит этой плоскости,
найдем
из условия принадлежит этой плоскости,
найдем
![]() .
.
![]() ;
;
![]() .
Уравнение плоскости
.
Уравнение плоскости
![]() .
Найдем
.
Найдем
![]() ,
точки
,
точки
![]() принадлежащей плоскости, тогда
принадлежащей плоскости, тогда
![]() ;
;
![]() .
Отсекаемый отрезок на оси
.
Отсекаемый отрезок на оси
![]() ,
или запишем уравнение плоскости в виде
,
или запишем уравнение плоскости в виде
![]() (уравнение плоскости в отрезках)
(уравнение плоскости в отрезках)
![]() или
или
![]() ,
как видим, отсекаемые отрезки осью
,
как видим, отсекаемые отрезки осью
![]() и
и
![]() равны 15, осью
равны 15, осью
![]() 10.
10.
Ответ: 10.
-
Найдите уравнение касательной плоскости к сфере
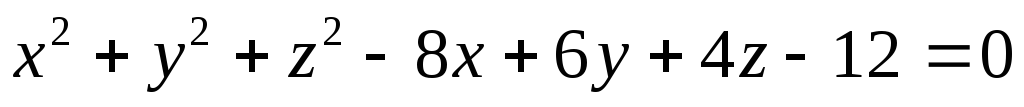 в точке
в точке
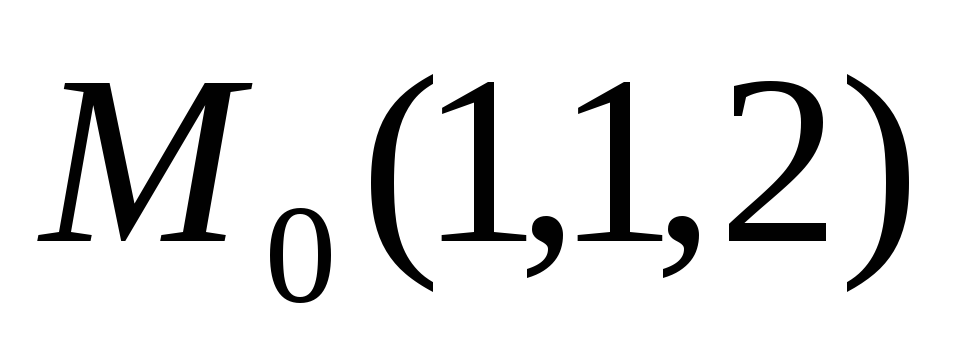 .
.
Решение: преобразуем уравнение
![]() ,
выделяя полные квадраты
,
выделяя полные квадраты
![]() ;
;
![]() .
Центр сферы в точке
.
Центр сферы в точке
![]() ,
,
![]() .
Вектор
.
Вектор
![]() ,
где
,
где
![]() -
точка касания, - вектор нормали касательной
плоскости
-
точка касания, - вектор нормали касательной
плоскости
![]() .
Тогда уравнение этой плоскости
.
Тогда уравнение этой плоскости
![]() ,
так как точка
,
так как точка
![]() принадлежит плоскости, то
принадлежит плоскости, то
![]() ,
,
![]() .
Тогда уравнение касательной плоскости
.
Тогда уравнение касательной плоскости
![]() или
или
![]() .
.
Ответ:
![]()
-
Дана кривая
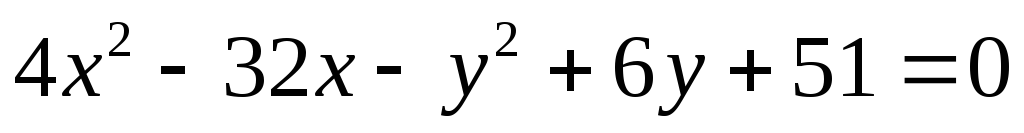 .
.-
Докажите, что эта кривая - гипербола.
-
Найдите координаты её центра симметрии.
-
Найдите действительную и мнимую полуоси.
-
Запишите уравнение фокальной оси.
-
Постройте данную гиперболу.
-
Решение: преобразуем уравнение
![]() ,
выделяя полные квадраты
,
выделяя полные квадраты
![]() ;
;
![]() .
Выделим новую систему координат
.
Выделим новую систему координат
![]() связанную
связанную
![]() уравнениями
уравнениями
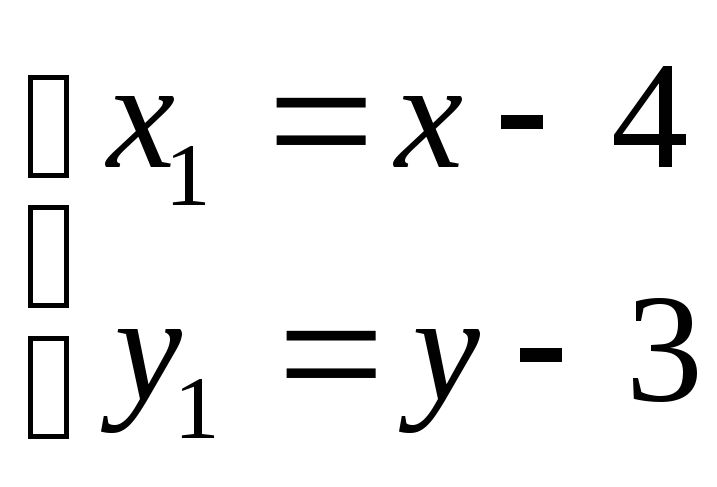 .
Получили:
.
Получили:
-
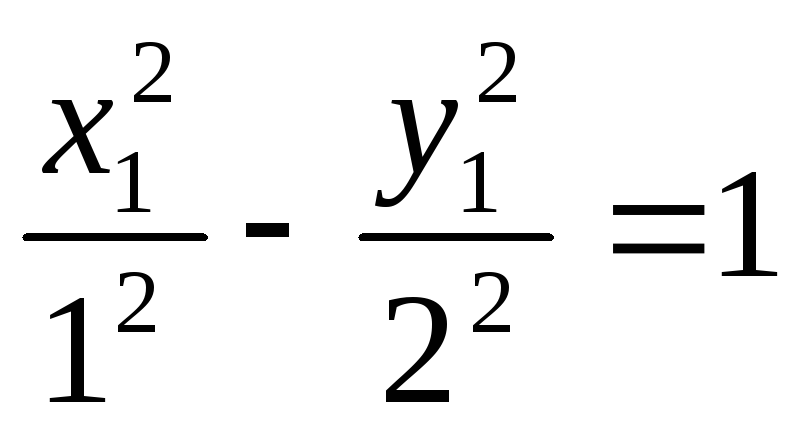 - каноническое уравнение гиперболы
- каноническое уравнение гиперболы
 ,
,
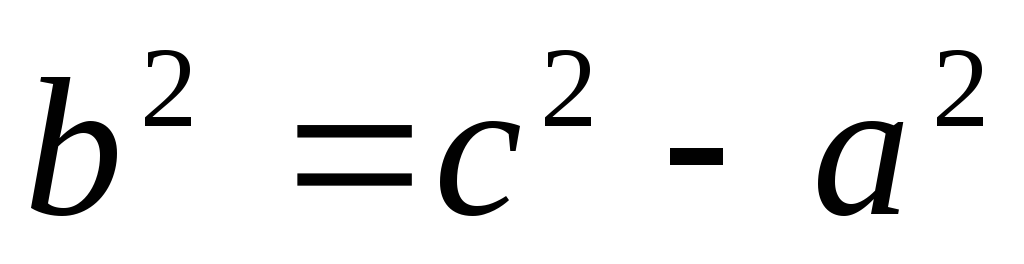 .
. -
Действительная ось
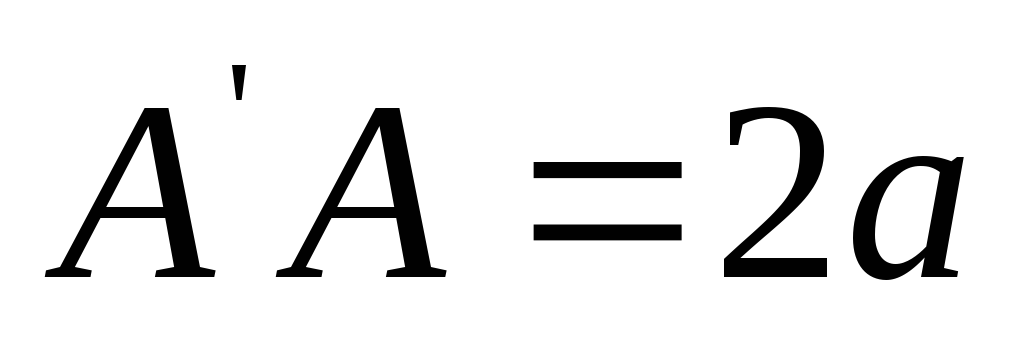 ,
мнимая ось
,
мнимая ось
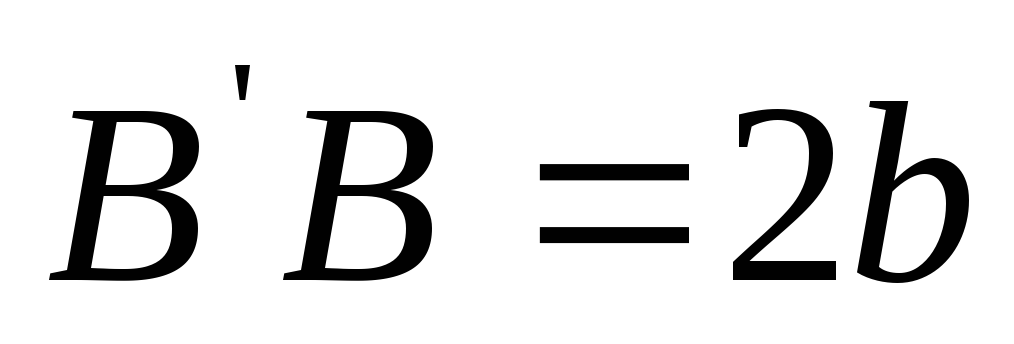 .
Действительная полуось
.
Действительная полуось
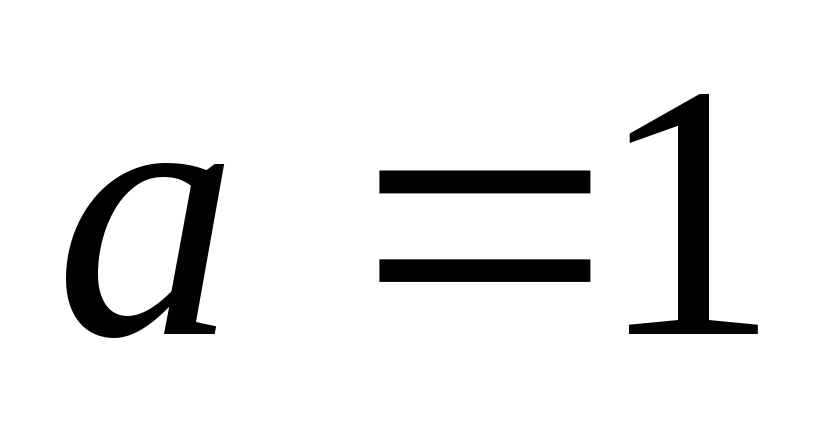 ,
мнимая полуось
,
мнимая полуось
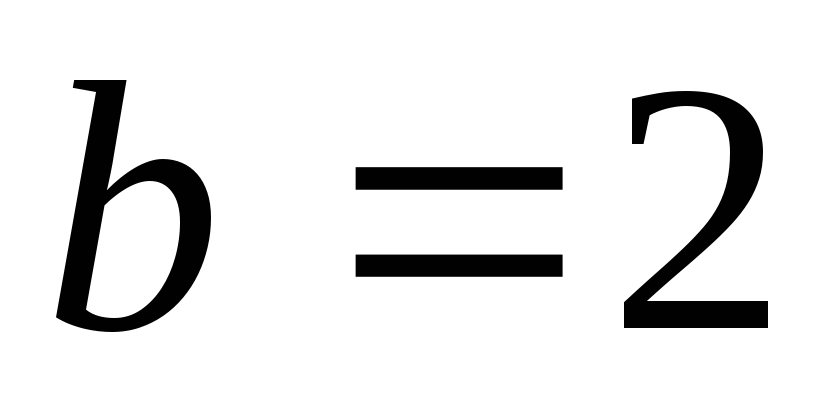 .
. -
Уравнение фокальной оси
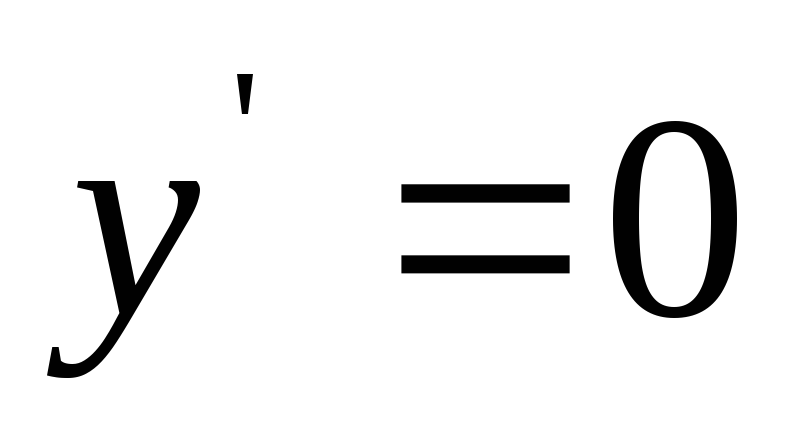 ,
,
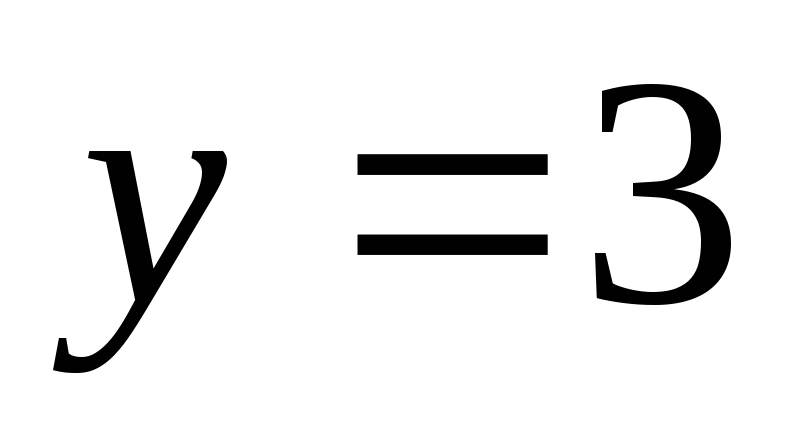 .
.
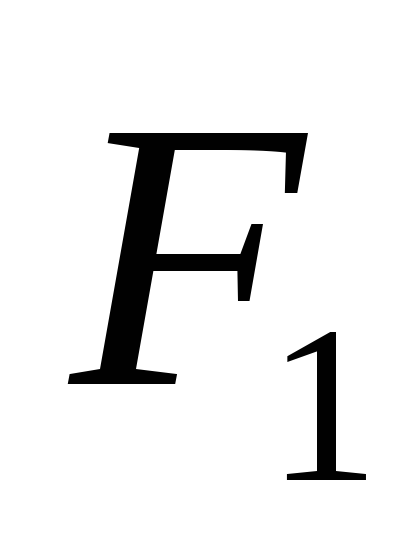 и
и
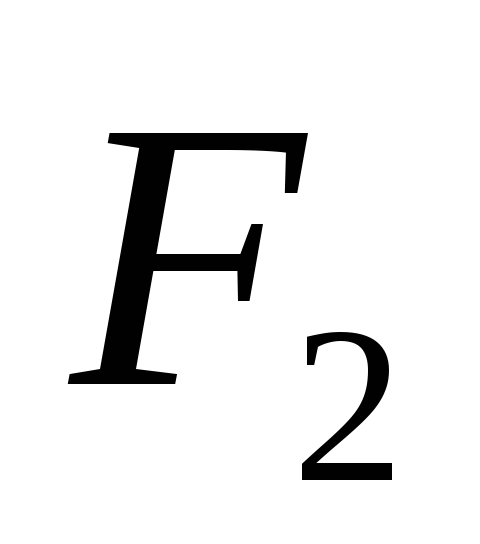 - фокусы гиперболы
- фокусы гиперболы
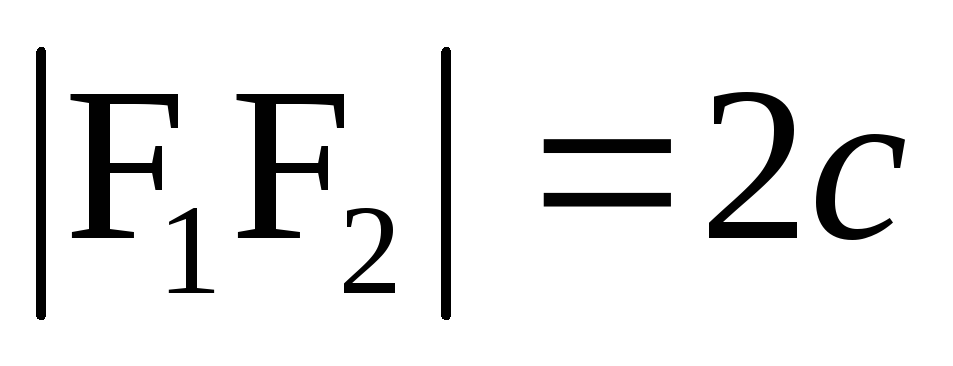 ,
,
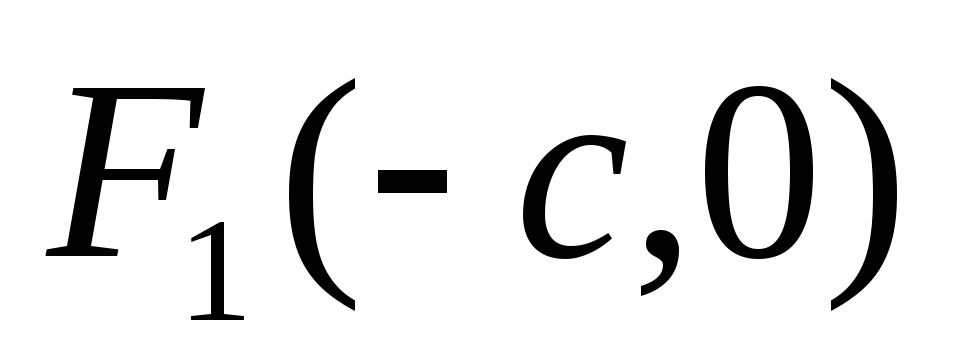 ,
,
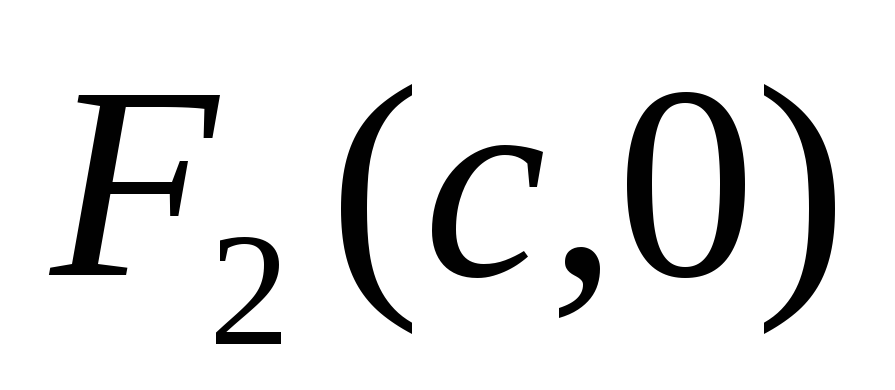 - в системе
- в системе
 ,
,
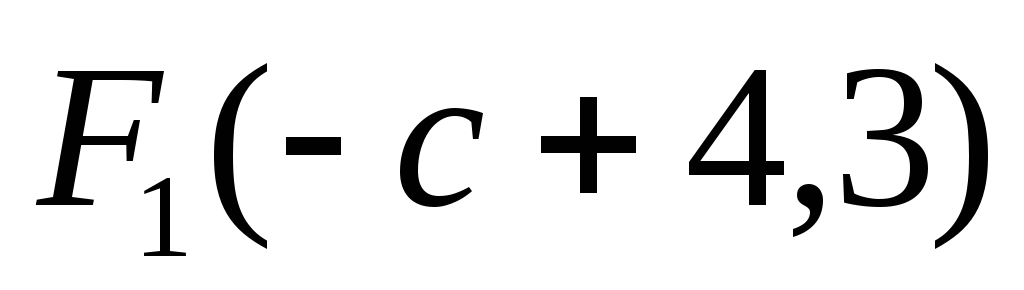 ,
,
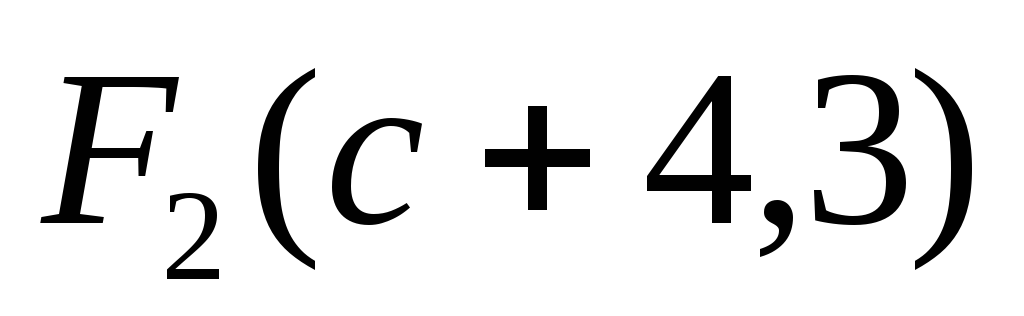 - в системе
- в системе
 .
.
 ,
,
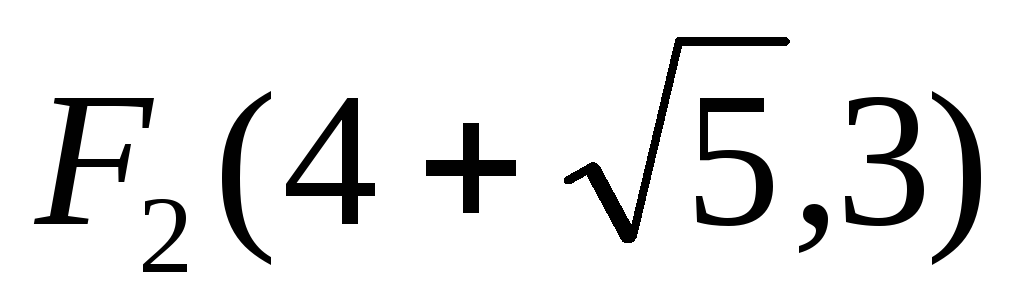 ,
так как
,
так как
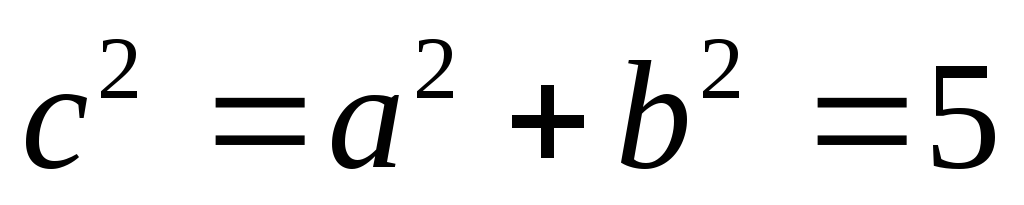 .
. -
Уравнение асимптот
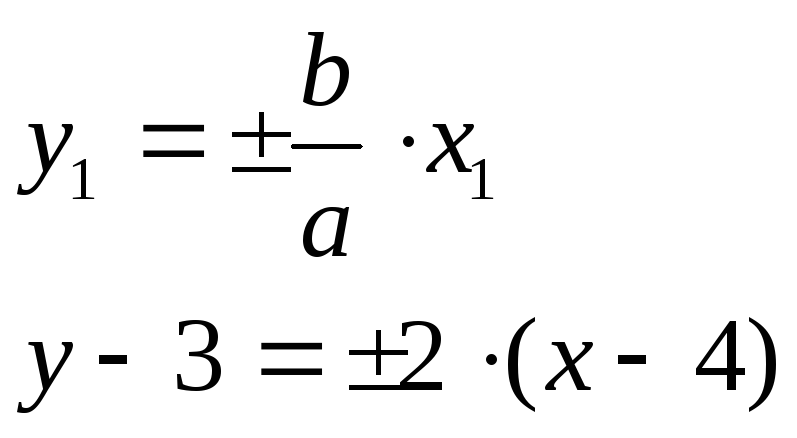 .
. -
Построение:
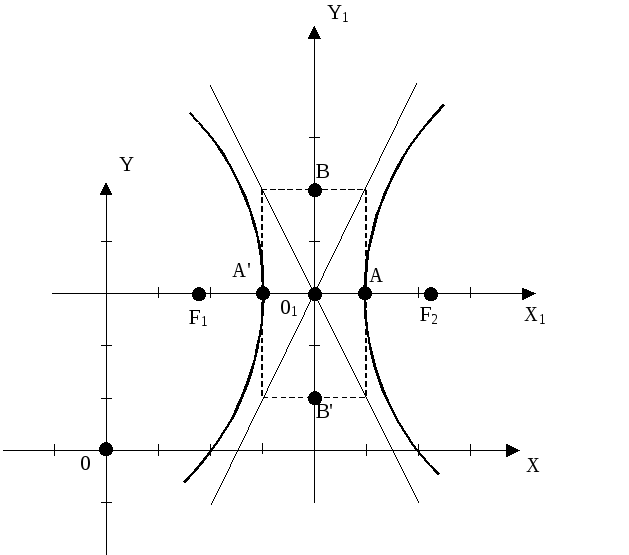
-
Дана кривая
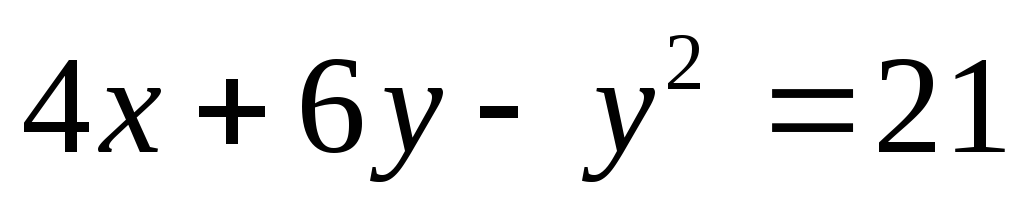 .
.-
Докажите, что данная кривая - парабола.
-
Найдите координаты её вершины.
-
Найдите значение её параметра
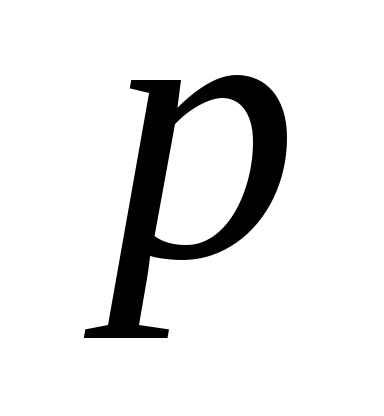 .
. -
Запишите уравнение её оси симметрии.
-
Постройте данную параболу.
-
Решение: преобразуем исходное
уравнение выделяя полные квадраты
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
Выделим новую систему координат
.
Выделим новую систему координат
![]() связанную с
связанную с
![]()
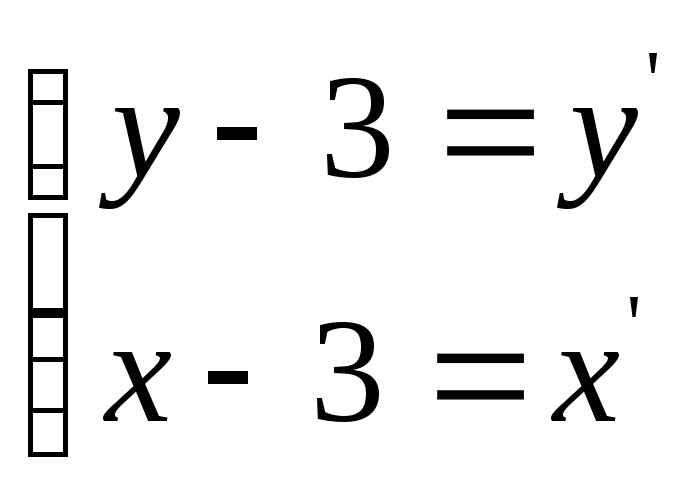 .
Уравнение примет вид
.
Уравнение примет вид
![]() - каноническое уравнение параболы, здесь
- каноническое уравнение параболы, здесь
![]() .
Вершина параболы
.
Вершина параболы
![]() ;
;
![]() .
.
![]() - ось симметрии.
- ось симметрии.
![]() .
.
Построение:
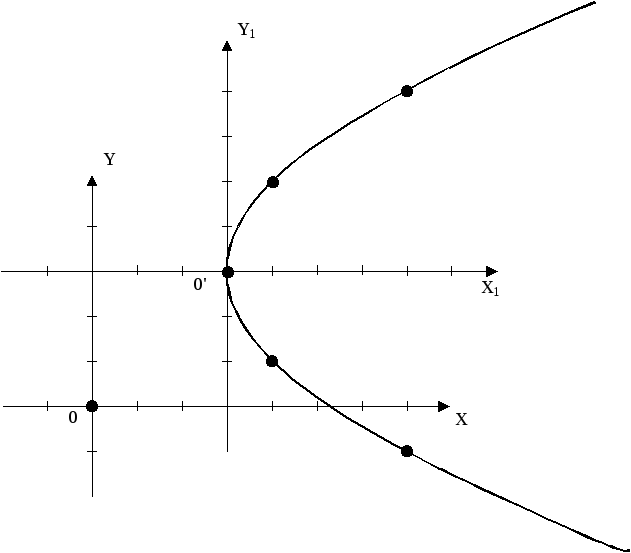
-
Дана кривая
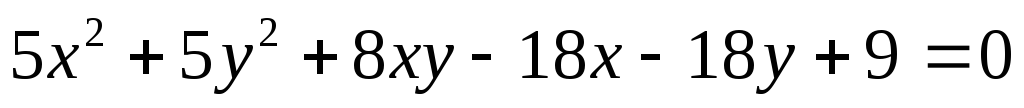
-
Докажите, что эта кривая – эллипс.
-
Найдите координаты центра его симметрии.
-
Найдите его большую и малую полуоси.
-
Запишите уравнение фокальной оси.
-
Постройте данную кривую.
-
Решение: Приводим квадратичную
форму
![]() к главным осям. Ее матрица
к главным осям. Ее матрица
![]() .
Записываем характеристическое уравнение
этой матрицы
.
Записываем характеристическое уравнение
этой матрицы
![]() ,
,
![]() .
Его корни
.
Его корни
![]() ,
,
![]() - являются собственными числами, так
как
- являются собственными числами, так
как
![]() ,
то кривая – эллипс. Координаты собственного
вектора, отвечающего числу
,
то кривая – эллипс. Координаты собственного
вектора, отвечающего числу
![]() ,
удовлетворяют уравнению
,
удовлетворяют уравнению
![]() .
В качестве базисного берем вектор
.
В качестве базисного берем вектор
![]() .
Другой базисный вектор
.
Другой базисный вектор
![]() .
Записываем матрицу перехода
.
Записываем матрицу перехода
![]() от базиса
от базиса
![]() к
к
![]() .
.
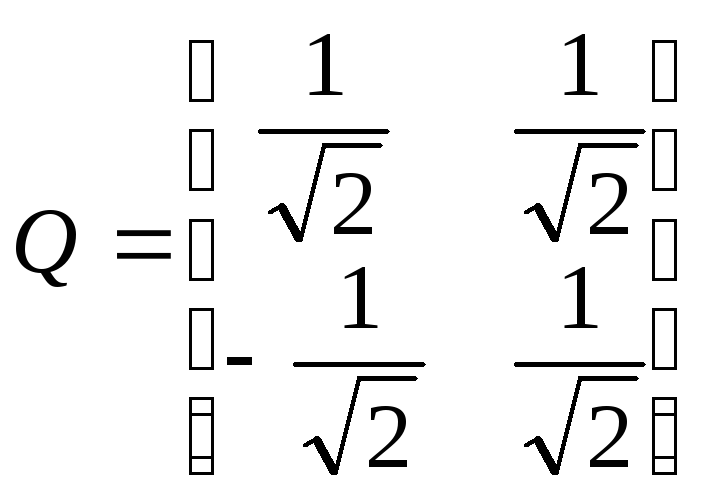 ,
тогда
,
тогда
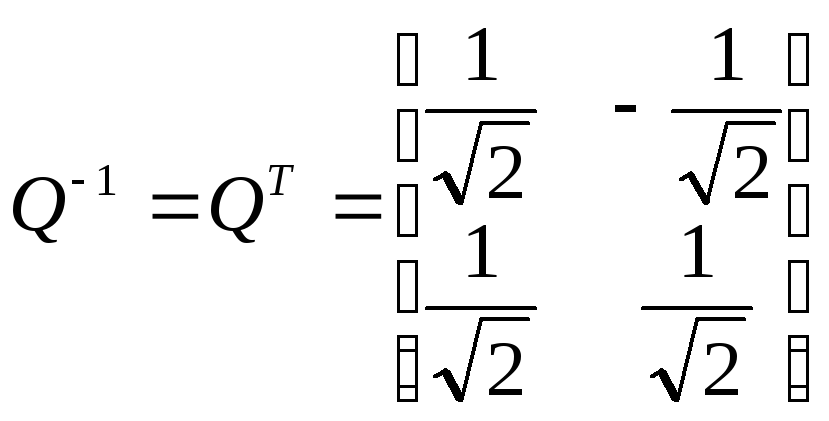 .
Новые координаты
.
Новые координаты
![]() связаны со старыми соотношениями
связаны со старыми соотношениями
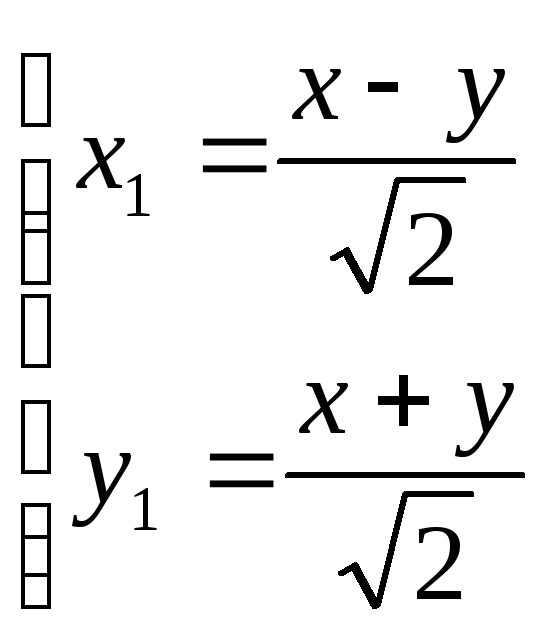 ,
,
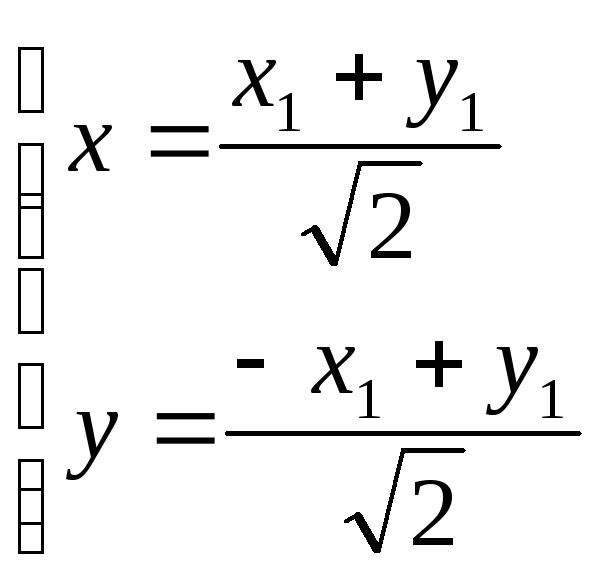 .
Уравнение в новой системе
.
Уравнение в новой системе
![]() или
или
![]() ,
,
![]() .
После выделения полных квадратов,
получаем
.
После выделения полных квадратов,
получаем
![]() Перейдем к новой системе координат
Перейдем к новой системе координат
![]() по
формулам
по
формулам
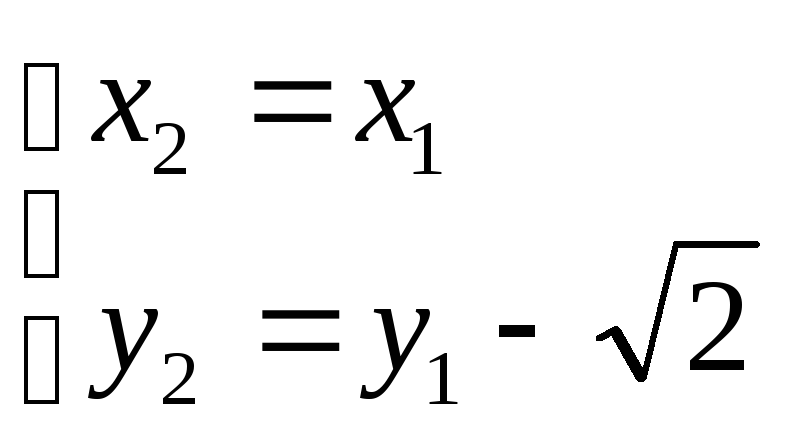 .
Теперь уравнение примет вид
.
Теперь уравнение примет вид
![]() ,
причем
,
причем
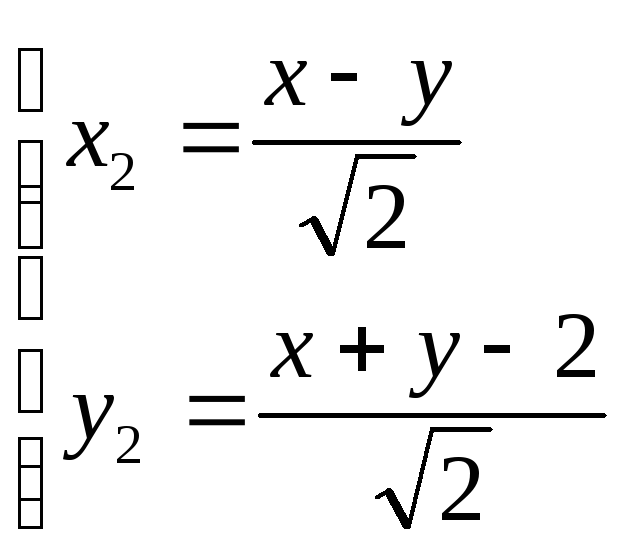 .
Решая систему
.
Решая систему
![]() ,
найдем координаты
,
найдем координаты
![]() нового начала
нового начала
![]() в старой системе координат. Строим
кривую. Для этого сначала в старой
системе строим новую систему координат.
Новые оси направленные по прямым
в старой системе координат. Строим
кривую. Для этого сначала в старой
системе строим новую систему координат.
Новые оси направленные по прямым
![]()
![]() и
и
![]()
![]() .
В системе
.
В системе
![]() строим эллипс. Зная уравнение
строим эллипс. Зная уравнение
![]() можно дать полную геометрическую
характеристику эллипса. Большая полуось
равна 3, малая - 1. Расстояние между
фокусами
можно дать полную геометрическую
характеристику эллипса. Большая полуось
равна 3, малая - 1. Расстояние между
фокусами
![]() .
Эксцентриситет
.
Эксцентриситет
![]() .
Уравнение фокальной оси
.
Уравнение фокальной оси
![]()
![]() .
.
Построение:
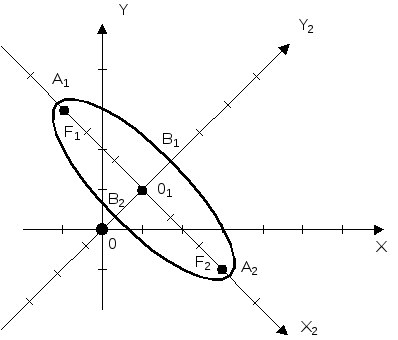
![]() -
центр симметрии;
-
центр симметрии;
![]() -
большая полуось;
-
большая полуось;
![]() - малая полуось;
- малая полуось;
![]() - фокус.
- фокус.
