Контрольная работа 2 / 2- 6_Высшая математика

МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ

ТОМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ СИСТЕМ УПРАВЛЕНИЯ И РАДИОЭЛЕКТРОНИКИ (ТУСУР)

Кафедра высшей математики

Контрольная работа № 2

по курсу "Высшая математика - 1"

Вариант 2.6

Преподаватель Студент группы

__________ / доц. Тупой И.И. / __________ / Пупкин В.И./

___________2002 г. до н.э. 35 ноября 2002 г. до н.э.

Томск 2002 до н.э.

Задача 1.

Записать общее уравнение прямой, проходящей через точку M(2, 4) перпендикулярно прямой 3x + 4y + 5 = 0.

Решение:

Обозначим через L общее уравнение прямой, проходящую через точку M(2, 4) и перпендикулярную прямой 3x + 4y + 5 = 0. В качестве вектора нормали прямой L можно принять любой вектор, перпендикулярный N₁(3, 4), так N₂(4, -3). Записываем искомое уравнение 4x - 3y - (4 ∙ 2 – 3 ∙ 4) = 0 или 4x - 3y + 4 = 0.

Проверка:

A₁ ∙ A₂ + B₁ ∙ B₂ = 0 (условие перпендикулярности прямых)

3 ∙ 4 + 4 ∙ (-3) = 0; 0 = 0

Ответ: 4x - 3y + 4 = 0.

Задача 2.

Составить уравнение прямых, проходящих через точку P(3, 5) на одинаковых расстояниях от точек A(-7, 3) и B(11, -15). В ответ ввести уравнение той прямой, которая отсекает от осей координат треугольник, расположенный в первой четверти.

Решение:

Так как прямая Ax + By + C = 0 проходит через точку P(3, 5), то 3A + 5B + C = 0, то, используя формулу

, где d - расстояние от точки до прямой

получим ,так как точки находятся

на равном расстоянии от прямой , или

|-7A + 3B + C| = |11A - 15B + C|, -7A + 3B + C = ± (11A - 15B + C)

-7A + 3B + C = 11A - 15B + C -18A + 18B = 0 A - B = 0

-7A + 3B + C = -11A + 15B - C 4A - 12B + 2C = 0 2A - 6B + С = 0

Составляем две системы уравнений:

Общее уравнение искомых прямых можно записать:

Ответ: 3x - 5y - 8 = 0

Задача 3.

Составить общее уравнение плоскости, проходящей через точки M₁(4, 2, 1) и M₂(3, 3, 2) параллельно вектору AB = (4, -3, -2).

Решение:

Данная плоскость параллельна векторам l₁ = M₁M₂ = (-1, 1, 1) и l₂ = AB = (4, -3, -2), поэтому ее вектор нормали

.

Запишем уравнение плоскости x + 2y – z + D = 0. Так как плоскость проходит через точки M₁ и M₂, находим D = 7.

Ответ: x + 2y - z + 7 = 0

Задача 4.

Найти координаты проекции начала координат на прямую

.

Решение:

1. Находим уравнение прямой (обозначим L).

2. 2) Найдем точку P(x₁, y₁), являющуюся: а) проекцией точки O(0, 0) на прямую L, б) точкой пересечения L и перпендикуляра OP, проходящего через точку O. Так как угловой коэффициент заданной прямой k₁ = -A/B = 3/4, то угловой коэффициент OP k₂ = B/A = - 4/3 (из условия перпендикулярности прямых k₁ = -1/k₂). Уравнение примет вид .

3) Вычислим координаты точки P, решая систему уравнений

Ответ: P(33/25, -44/25).

Задача 5.

При каком значении параметра С прямая (а) параллельна плоскости .

Решение:

а) Так как , то неизвестное z системы (а) можно принять в качестве свободного и записать 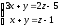. Находим общее решение этой системы, выражая x и y через z . Примем z = t и запишем параметрические и канонические уравнения прямой.

б) Из условия задачи прямая и плоскость параллельны, значит угол φ между ними равен нулю и . В результате имеем .

Ответ: C = -2

Задача 6.

Две грани куба лежат на плоскостях 3x – 6y + 2z – 5 = 0 и 3x – 6y + 2z + 30 = 0. Найти объем куба.

Решение:

Грани куба лежат на параллельных плоскостях, так как отношения коэффициентов при соответствующих переменных пропорциональны т. е. 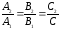. Чтобы найти объем куба, нужно вычислить ребро, а это расстояние между плоскостями. Возьмем точку M(0; 0; 2,5) принадлежащей плоскости 3x - 6y + 2z – 5 = 0 и найдем расстояние d между точкой M и плоскостью 3x – 6y + 2z + 30 = 0

Ответ: Объем куба равен 125.

Задача 7.

Доказать, что уравнение x² + y² + z² - 4x + 6y - 8z - 35 = 0 определяет сферу. Найти координаты (x₀, y₀, z₀) ее центра и радиус R. В ответе записать четверку чисел (x₀, y₀, z₀, R).

Решение:

Преобразуем данное уравнение, выделив полные квадраты:

.

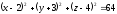Следовательно, данное уравнение определяет сферу с центром в точке C(2, -3, 4) и радиуса R = 8.

Ответ: (2, -3, 4, 8)

Задача 8.

Дана кривая 25x² + 16y² – 350x + 825 = 0.

1. Доказать, что кривая – эллипс.

2. Найти координаты центра его симметрии.

3. Найти его большую и малую полуоси.

4. Записать уравнение фокальной оси.

5. Построить данную кривую.

Решение:

1. Преобразуем уравнение кривой, выделив полные квадраты:

Вводим новые переменные

или - каноническое уравнение эллипса.

2) Центр симметрии находится в точке (7, 0).

3) Большая полуось , малая полуось .

4) Фокальной осью является ось абсцисс, т. е. y = 0

5)

Задача 9.

Дана кривая 14 y = ( x - 8 )².

1. Доказать, что данная кривая – парабола.

2. Найти координаты ее вершины.

3. Найти значение ее параметра p.

4. Записать уравнение ее оси симметрии.

5. Построить данную параболу.

Решение:

1. Раскроем скобки: 14y = x² - 16x + 64. Заменим x на (x₁ + a) и y на (y₁ +b), где a и b – координаты вершины параболы. Выбираем a и b так, чтобы коэффициенты при x₁ и свободном члене были равны нулю.

14(y₁ + b) = (x₁ + a)² - 16(x₁ + a) + 64

14y₁ – x₁² – 2x₁(a – 8) + (14b + 16a – 64 – a²) = 0

a – 8 = 0 и	14b + 16a – 64 – a2 = 0
a = 8	b = 0

14y₁ – x₁² = 0

x₁² = 14y₁ – каноническое уравнение параболы.

2. x₀ = 8, y₀ = 0 – координаты вершины параболы.

3. p = 7.

4. Осью симметрии является прямая, проходящая через точку (8, 0) и параллельная оси ординат, т. е. x = 8.

5)

Задача 10.

Дана кривая x² + y² + 3xy + x + 4y = 0,5.

1. Доказать, что эта кривая – гипербола.

2. Найти координаты ее центра симметрии.

3. Найти квадраты ее действительной и мнимой полуосей.

4. Записать общее уравнение фокальной оси.

5. Построить данную гиперболу.

Решение:

1. Если кривая второго порядка задана уравнением Ax² + 2Bxy + Cy² + 2Dx + 2Ey +F = 0, то, применив преобразование поворота осей координат на угол α, с использованием формул x = x'cos α - y'sin α, y = x'sin α - y'cos α, следует при надлежащем выборе α освободиться в уравнении от члена с произведением координат. Так как по условию задачи A = C = 1, то угол α находим из формулы:

, отсюда

и

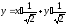
, примем ,

получим - каноническое уравнение гиперболы, сопряженной с

Произведем преобразование параллельного переноса системы координат в новое начало O' по формулам . Оси O'x'' и O'y'' направлены по прямым y = - x – 1 и y = x + 3.

2. Центром симметрии гиперболы является точка с координатами (-2, 1)

3. a² = 1/5, b² = 25

4. Уравнение фокальной оси y = - x - 1