Контрольная работа 2 / 2- 4.6_Высшая математика
.docТомский межвузовский центр дистанционного образования
Томский государственный университет
систем управления и радиоэлектроники (ТУСУР)
Контрольная работа № 2
По дисциплине «Высшая математика»
( Учебное пособие «Высшая математика. Введение в
математический анализ. Дифференциальное исчисление», Л.И. Магазинников, А.Л. Магазинникова, 2003 г.)
Выполнил:
Студент ТМЦДО
специальности
Вариант 4.6
1. Найти производные от данных функций:
а)
,
;
б)
,
;
в)
,
.
Решение: а)
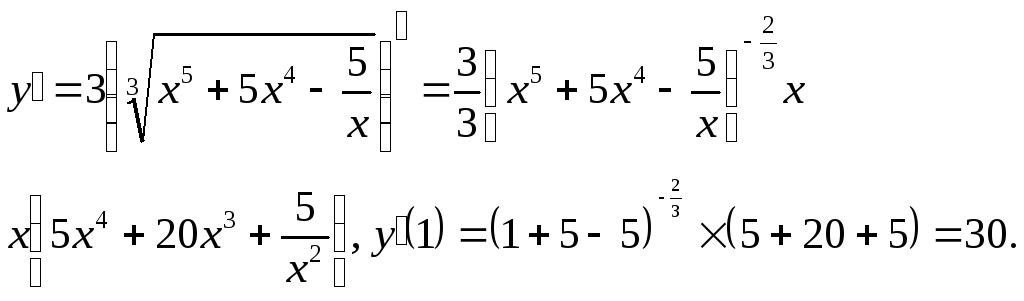
Ответ 30.
Решение: б)
.
.
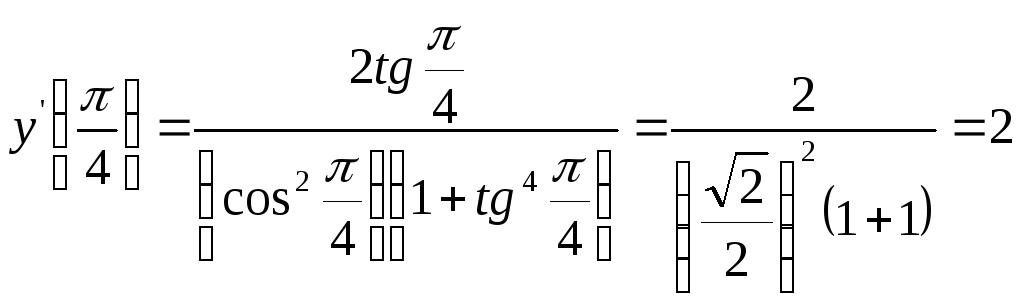Ответ 2.
Решение: в)
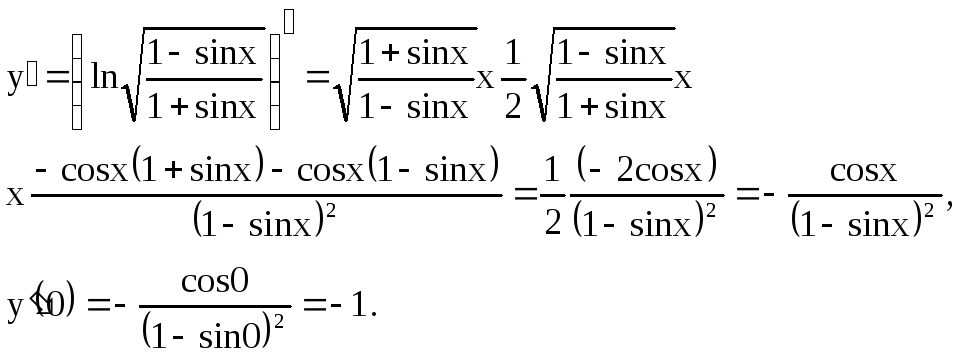
Ответ -1.
2.Дана функция
.
Найти
.
Вычислить
.
Решение:
,
.
,
.
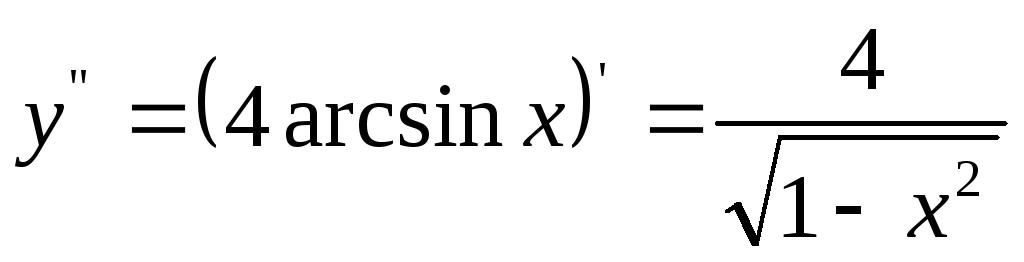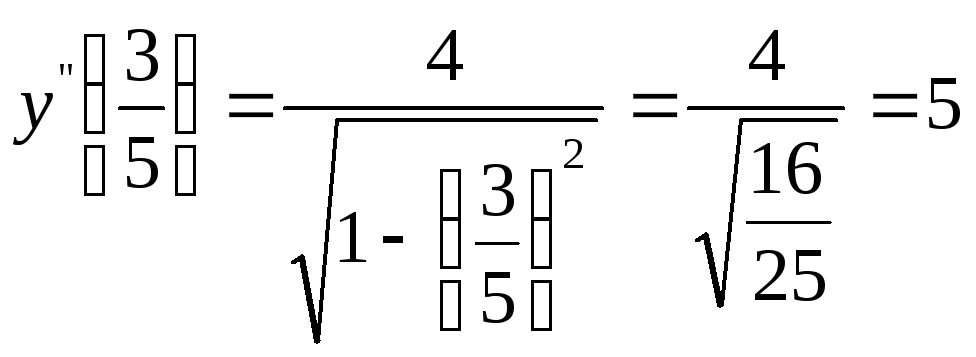
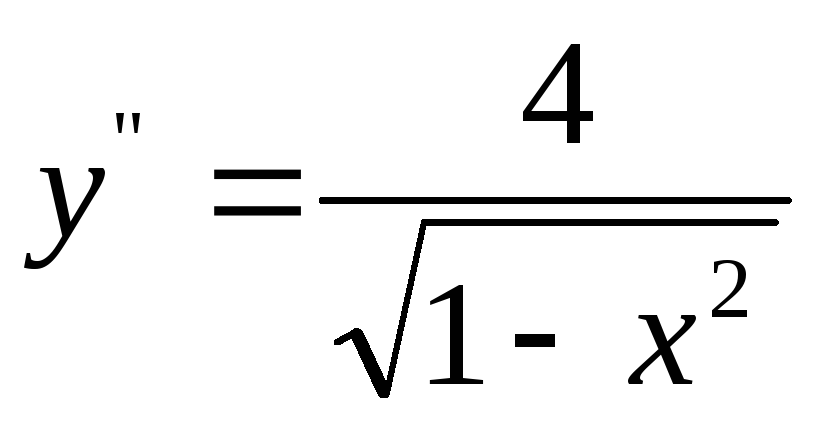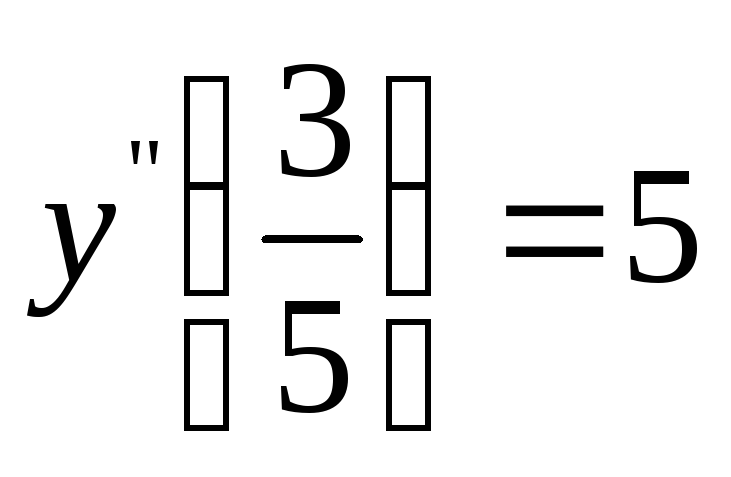Ответ 5.
3. Дана функция
.
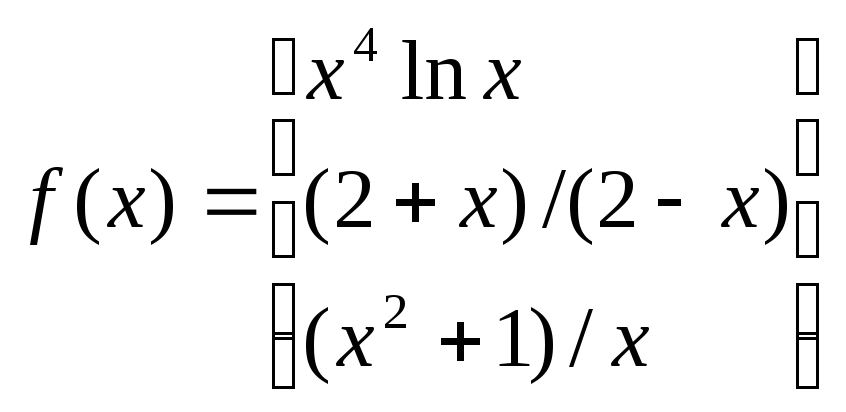Найти
и
.
Вычислить
и
.
Решение:
найти производную от
, далее найти производные от координатных
функций.
,
.
,
.
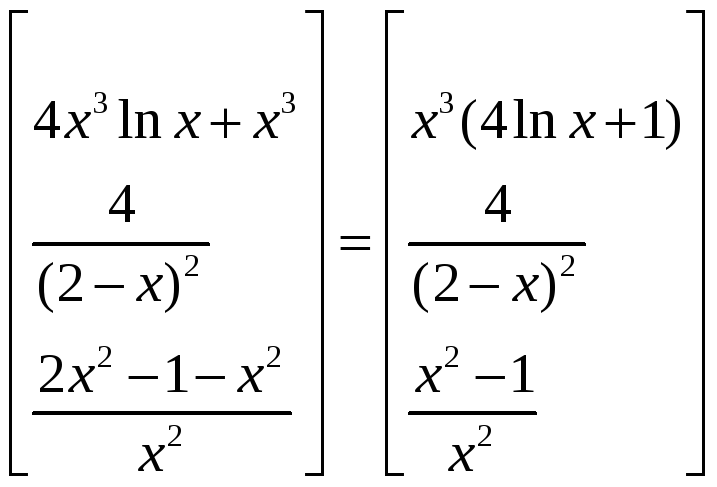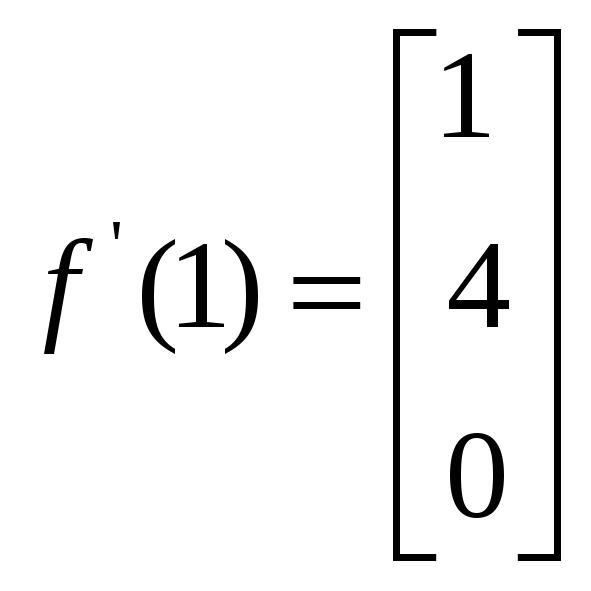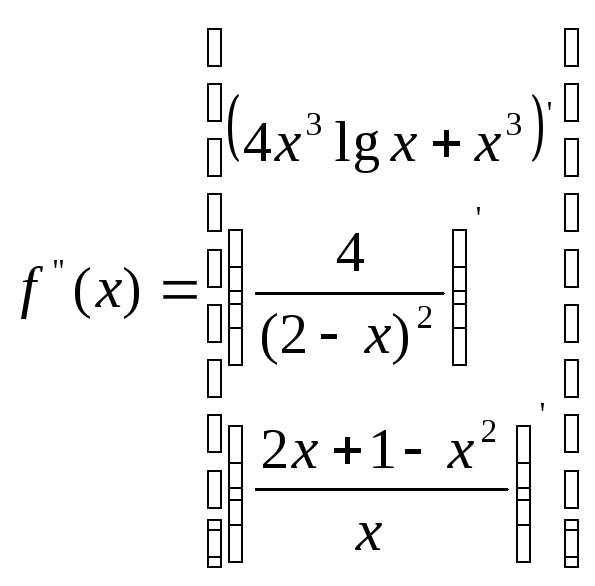
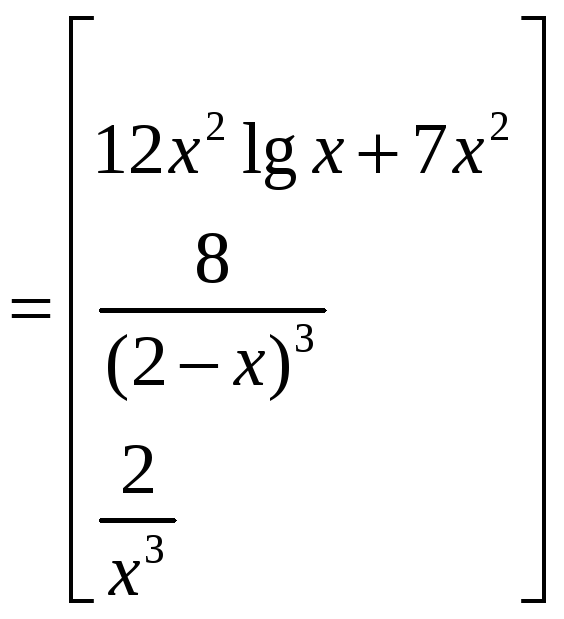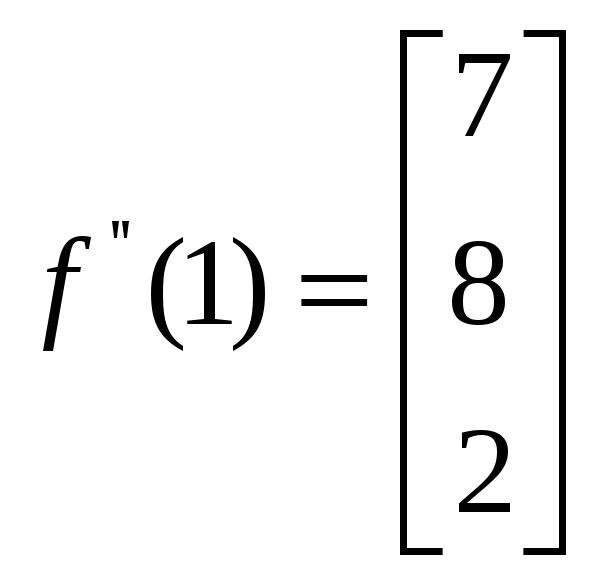Ответ:
,
.
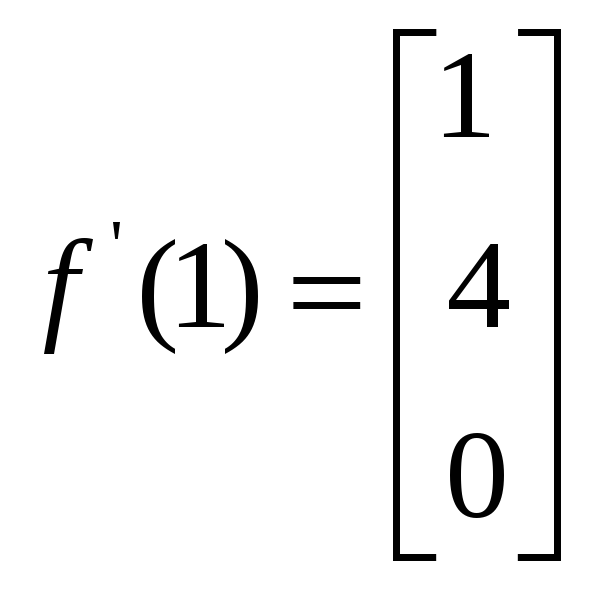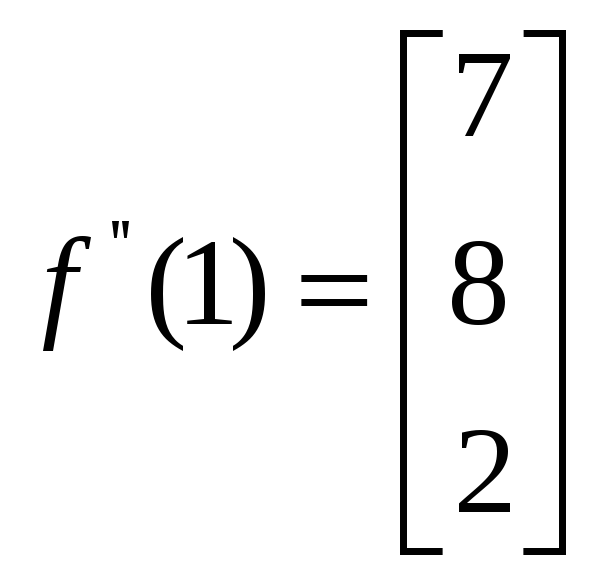4. Доказать, что функция z = exy удовлетворяет уравнению
.
Решение:
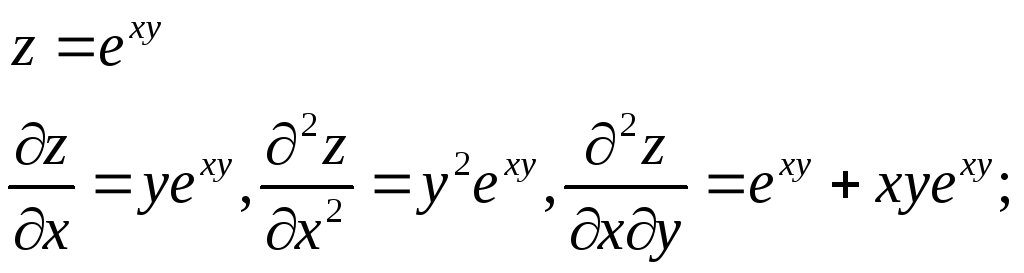
5. Дана
функция
.
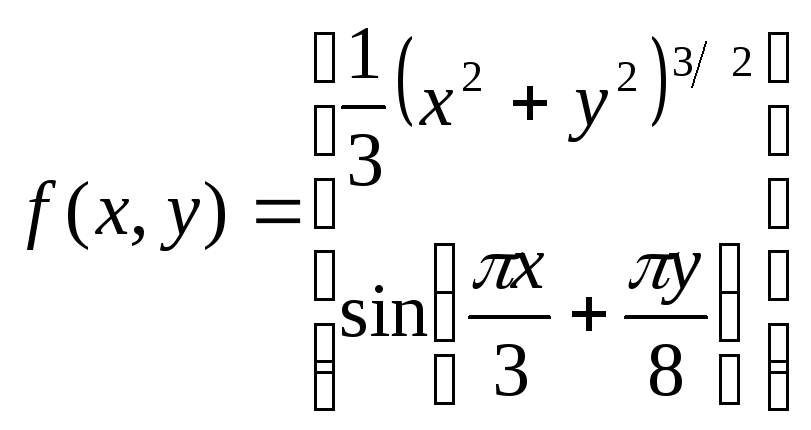Найти
.
Вычислить
.
В ответ ввести сумму элементов
матрицы
.
Решение:
,
.
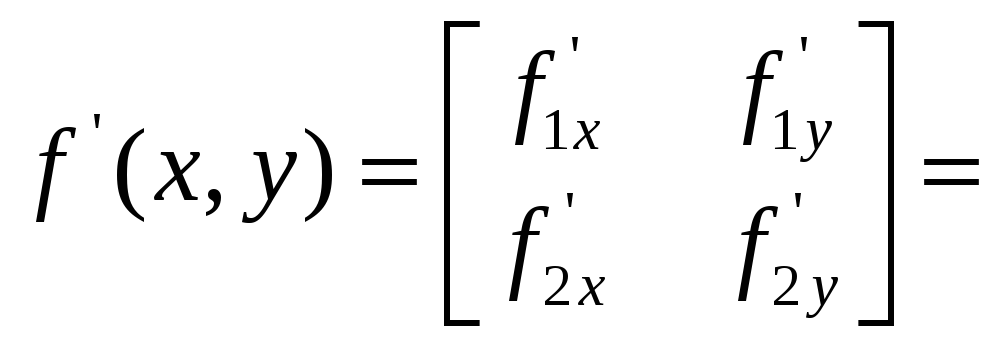
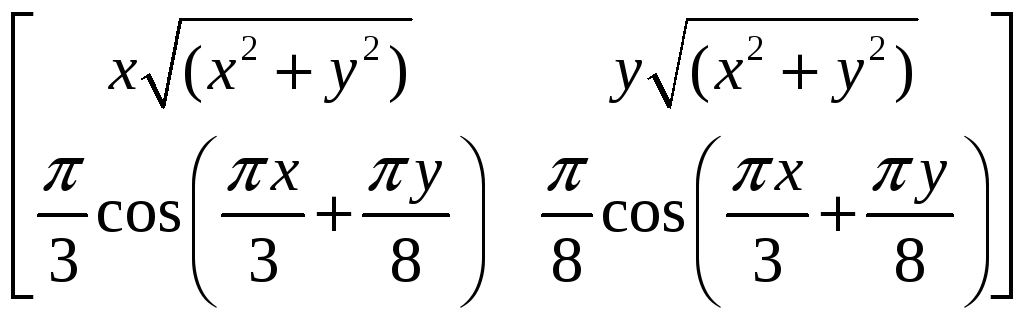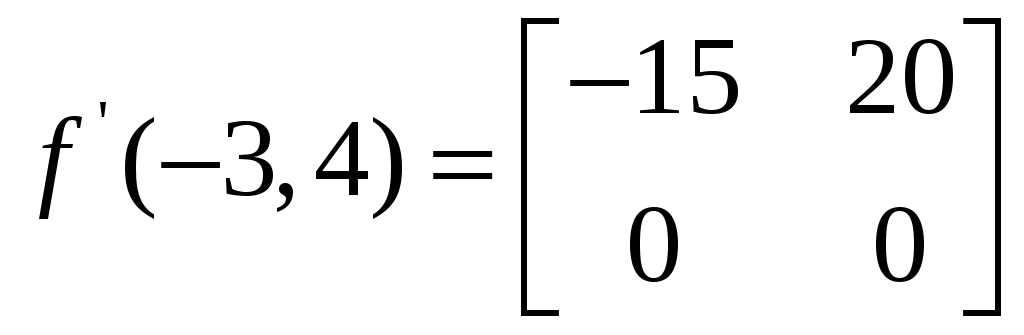Сумма элементов
матрицы:
.
Ответ:
.
6.
Дана функция
Найти:
а) Координаты
вектора grad
u
в точке M
б)
в точке M
в направлении вектора
Решение:а)
найдем grad
u
в точке
:
;
;
;
;
;
;
Таким образом, в точке М grad u = (–10,–15,–1).
б) найдем орт вектора а:
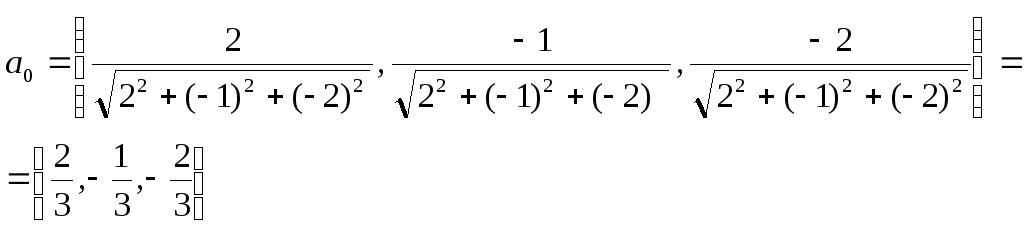
значит
;
Ответ: grad
u
= (–10,–15,–1),
.
7.
Найти
,
если
.
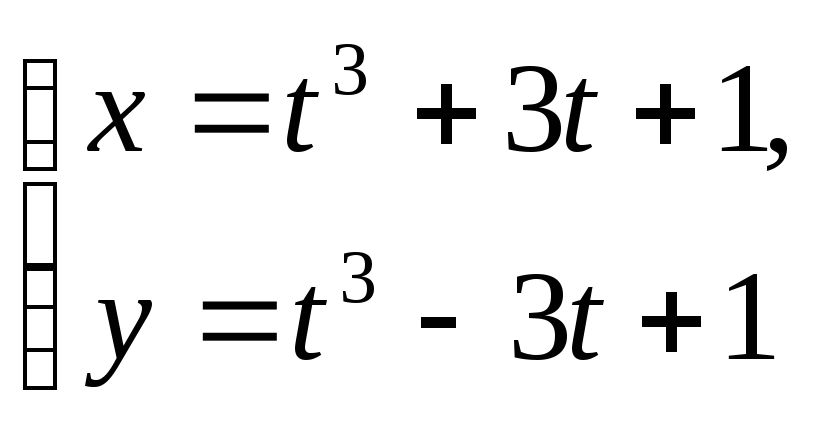Вычислить
,
если t=1.
Решение:
найдем
и
:
,
,
,
.
,
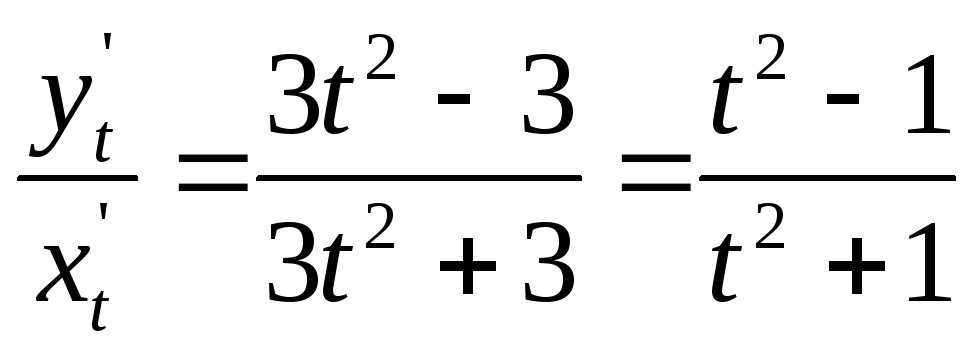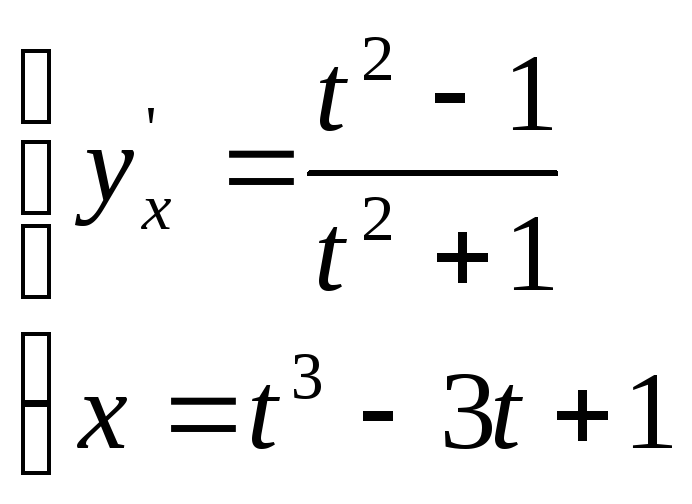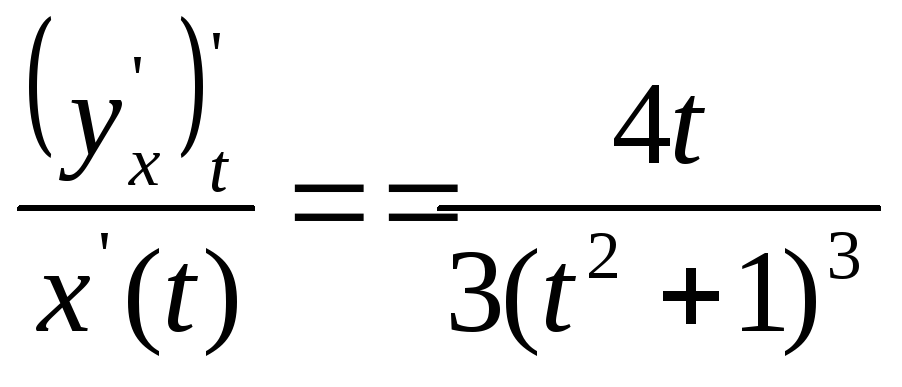
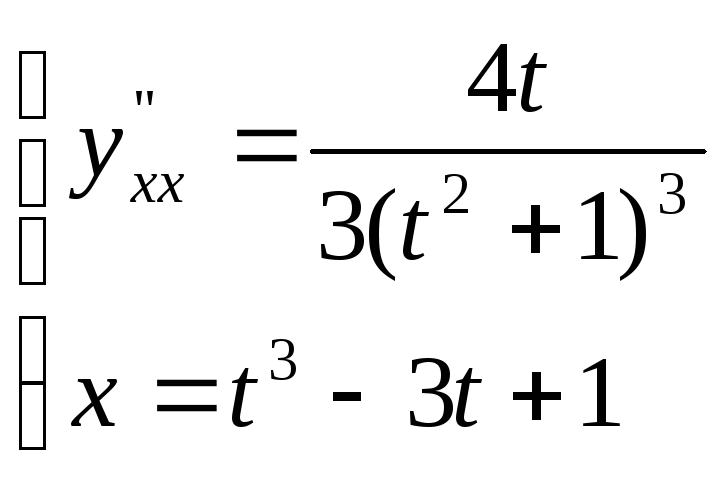при t=1
вторая производная
Ответ:
.
8)
Функция
задана неявно уравнением;
Вычислить: а)
;
б)
Решение:
а)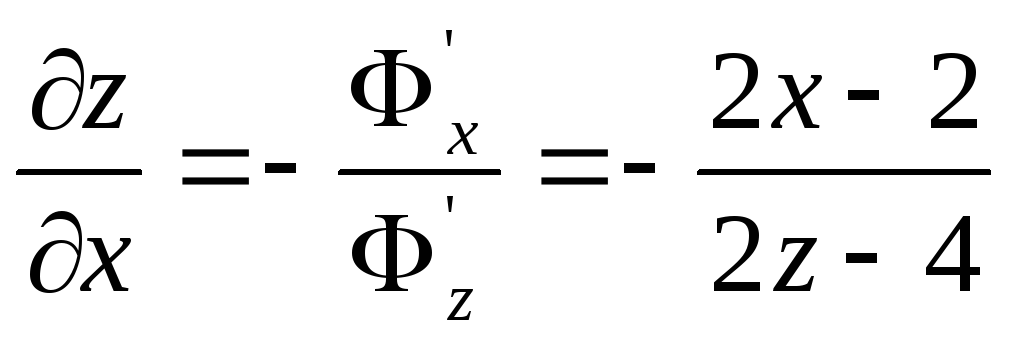
,
б)
,
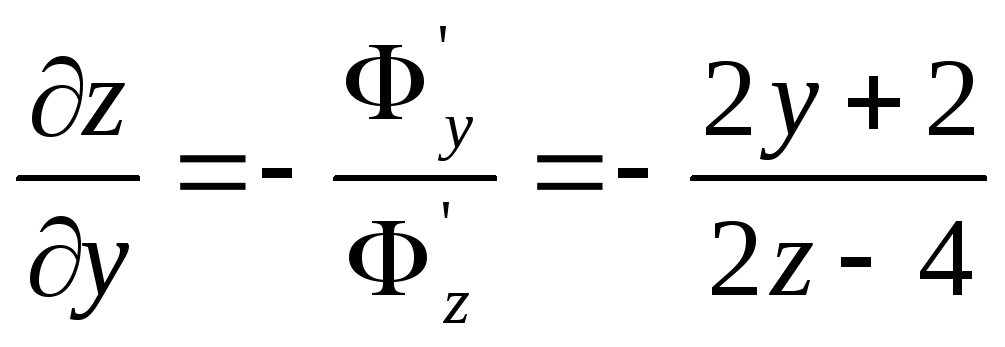Ответ:
,
.
9) К графику
функции
в
точке с абсциссой x=0
проведена касательная. Найти абсциссу
точки графика касательной, ордината
которой равна 19.
Решение: Уравнение касательной к графику функции y = f(x) в точке x0 = 0
имеет вид:
,
,
.
Запишем уравнение касательной :
или
,
из полученного уравнения найдем абсциссу
касательной, если ордината равна 19.
,
.
Ответ:
10)
Найти
,
если
.
Вычислить значение
,
если
Решение:
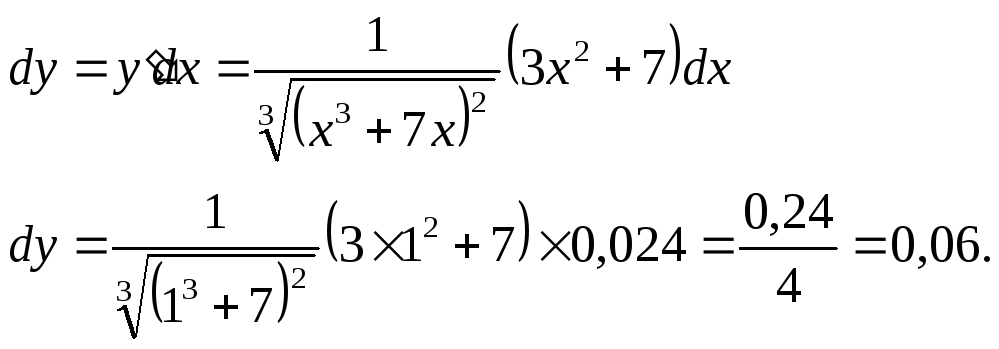
Ответ:
=0,06
11)
Дана функция
и точки
.
Вычислить
при
переходе из точки
в точку
(ответы округлить до сотых).
Решение:
z = z(M1) – z(M0) = 1,982 + 3,912 + 21,98 + 3,91 – 1 – 22 – 42 – 22 – 4 + 1 = –0,92;
при переходе из точки М0 в точку М1 x = –0,02; y = –0,09;
=
(2x + 2)dx + (2y + 1)dy
(2x + 2)x
+ (2y + 1)y
=
= (22 + 2)–0,02 + (24 + 1)–0,09 = –0,12 – 0,81 = –0,93.
Ответ:z –0,92; dz –0,93.
12)
Дана функция
найти её наибольшее и
наименьшее
значения на отрезке
Решение: Сначала найдем значение функции на концах промежутка:
C помощью производной найдем экстремумы:
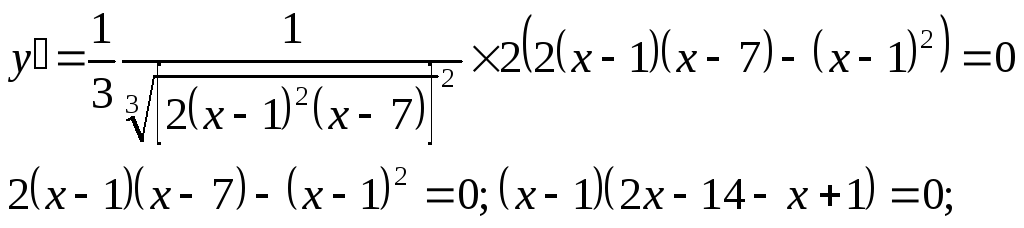
Наибольшее
значение функции
.
На отрезке
принадлежит
максимуму
этой функции
.Наименьшее значение функции будет на
краях отрезка
и их
значение
13) Дана функция z = xy. Найдите ее наибольшее и наименьшее значение в
круге x2 + y2 ≤ 4.
Решение:
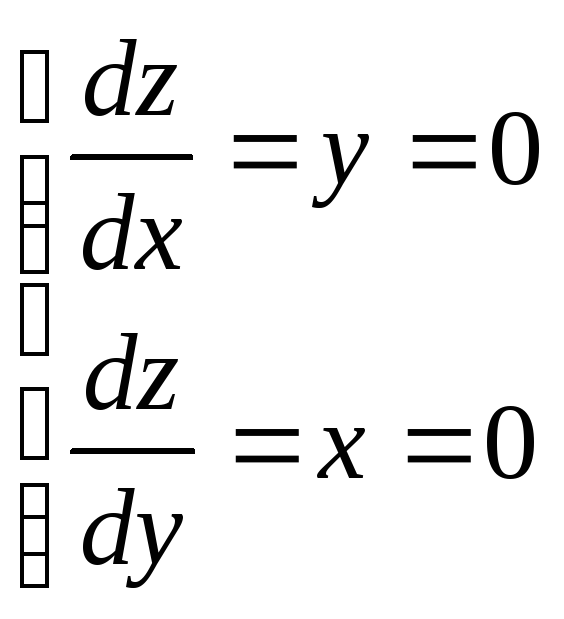
Находим из условия равенства нулю частных производных
единственную cтационарную точку М0 (0, 0), расположенную внутри
круга x2 + y2 ≤ 4, z(0,0) = 0. Для отыскания наибольшего и наименьшего
значений на
окружности
составим
функцию Лагранжа и найдем точки,
в которых возможны наибольшее и наименьшее значение. Из системы
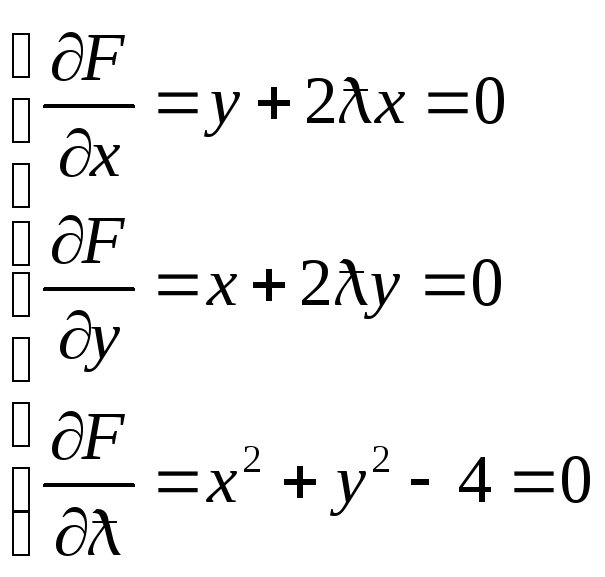
Получаем четыре
точки:
При этом
,
.
Сравнивая значение функции в этих
критических точках, видно, что наименьшее
значение функции достигается в точках
М2
М3
и равно -2, а наибольшее - в точках М1
и М4 и
равно 2.
14)
Провести полное исследование функции
и начертить её
график.
Решение:
1. Область
определения функции
.
Область значения функции
.
2.Функция
общего
вида, не является ни четной, ни нечетной.
3.Данная функция непериодическая.
4.Функция
непрерывна на всей числовой оси, кроме
точки x
= 0, где знаменатель обращается в нуль.
Так как
не существует, то разрыв второго рода.
Точка х =
0 – вертикальная асимптота.
5.Находим наклонные
асимптоты
:
,
.
6. Находим
производную
:
,
Производная
обращается в нуль только в точке
.
На участке
производная
отрицательна, следовательно, функция
убывает, а на участке
производная положительна, следовательно,
функция возрастает. Если
,
,
следовательно, функция убывает. В точке
имеем
минимум функции, равный
1,89.
Находим
:
При
,
,
следовательно, график функции выпуклый
вниз.
на всей числовой оси. График функции
везде вогнут.
Строим график:
