Контрольная работа 2 / 2- 3_Высшая математика_3

Министерство образования

Российской Федерации

ТОМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

СИСТЕМ УПРАВЛЕНИЯ И РАДИОЭЛЕКТРОНИКИ (ТУСУР)

ТМЦ ДО

Кафедра высшей математики

Контрольная работа №2

2003

Контрольная работа № 2.

Вариант 2.3

1.(2С3.РП). Записать общее уравнение прямой, проходящей через точку М (-2,4) перпендикулярно прямой х+2у+5=0. (2Д3). Найти площадь треугольника, образованного данной прямой с осями координат.

1. l₁: x+2y+5=0

l₂ – искомая прямая, l₂+l₁

₁ M (-2;4)є l₂

k₁= - - угловой коэф-нт прямой l₁

² ₁

l₂┴ l₁, тогда k₂ = - = 2

k₁

Уравнение прямой l₂, проходящей через т. М (-2;4) с угловым коэф-ом k₂=2 имеет вид:

L₂: y-y_m=k₂ (x-x_m);

y-4 = 2(x+2);

Запишем это уравнение прямой в отрезках:

2x-y = -8;

_{x y}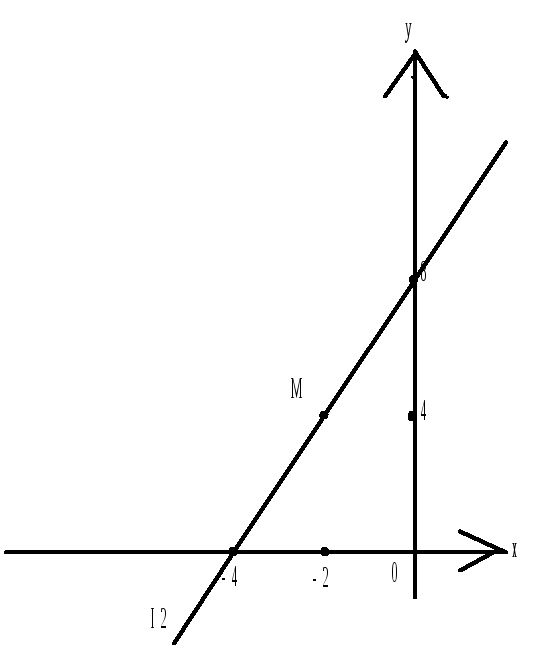

_-4 + ₈ = 1

Тогда площадь треугольника, образованного данной прямой с осями

координат равна

S = ¹ * 4*8* = 16 кв. Ед.

²

2.(Р43.РП). Записать общее уравнение прямой, проходящей через точку М(-2,2) и отсекающей от первого координатного угла треугольник площадью S = 4,5 кв. ед.

Уравнение прямой в отрезках:

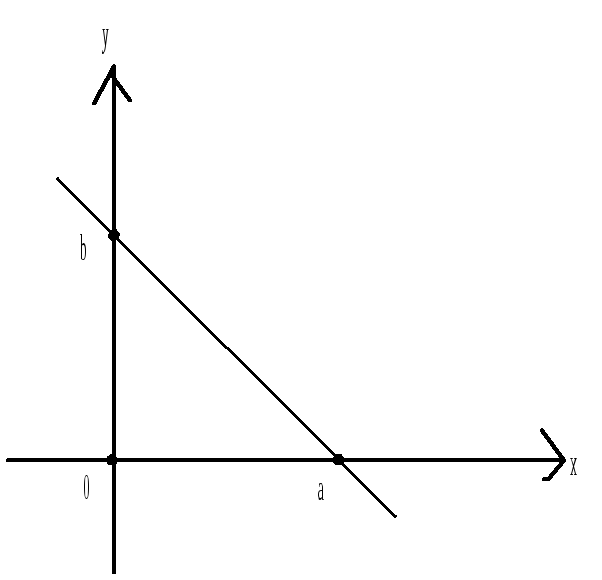
_{x y}

l: _a + _b = 1

S = ¹ ab = 4,5 , ab = 9

²

Прямая проходит через точку M (-2;2), значит^{, -2} + ² или –2b + 2a = ab

^{а b}

Решаем систему:

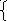ab = 9 a>0

-2a + 2b = ab b>0

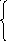₉

b= _a

₁₈

-2a + _a =9

-2a² –9a – 18 = 0,

2a² + 9a – 18 = 0;

D = √225 = 15

_{-9-15 24}

a ₁ = ₄ = - ₄ = -6 < 0

_{-9+15 3}

a ₂ = ₄ = ₂

₉

b = _3/2 = 6

Тогда уравнение прямой имеет вид:

_{x y}

+ =1;

^{3/2 6}

_{2x y}

₃ + ₆ = 1;

l: 4x+y-6=0

3.(Т33.БЛ). Даны вершины треугольника А(2,1,0), В(3,-1,1) и С(1,2,-4). Записать общее уравнение плоскости, проходящей через сторону АВ перпендикулярно плоскости треугольника АВС.

А (2;1;0)

В (3;-1;1)

С (1;2;-4)

A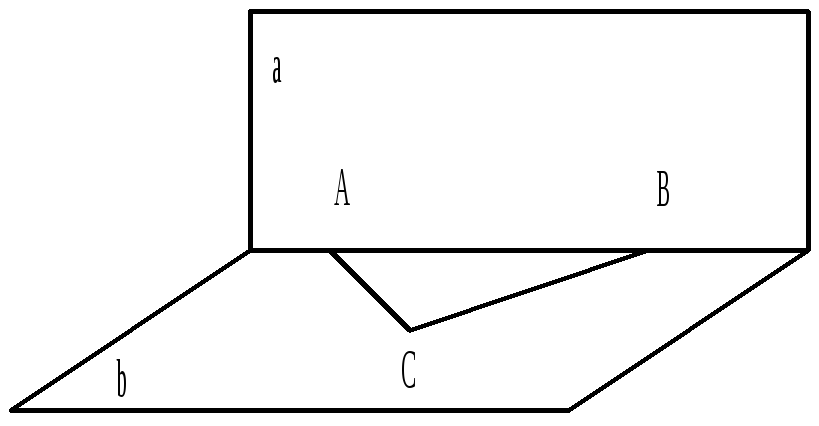B є 

  . Найти уравнение пл. 

N _α – нормальный вектор пл. 

N _α =AC * BC

AC = (-1;1;-4), BC = (-2;3;-5)

i j k

N_α = -1 1 -4 = 7i + 3j –k = (7;3;-1)

-2 3 -5 Плоскость α проходит через т. А (2;1;0) и ее нормальный вектор N_α = (7;3;-1), значит ее уравнение имеет вид:

7(х-2) + 3 (у-1)-1 (z-0) = 0;

α: 7x+3y-z –17 =0

4.(839).Найти расстояние от точки Р (1,2,0) до прямой х-8 = у-1 = z .

^{3 -4 0}

P (1;2;0)

l: х-8 = у-1 = z

^{3 -4 0}

Через т. Р проводим пл – ть α перпендикулярно

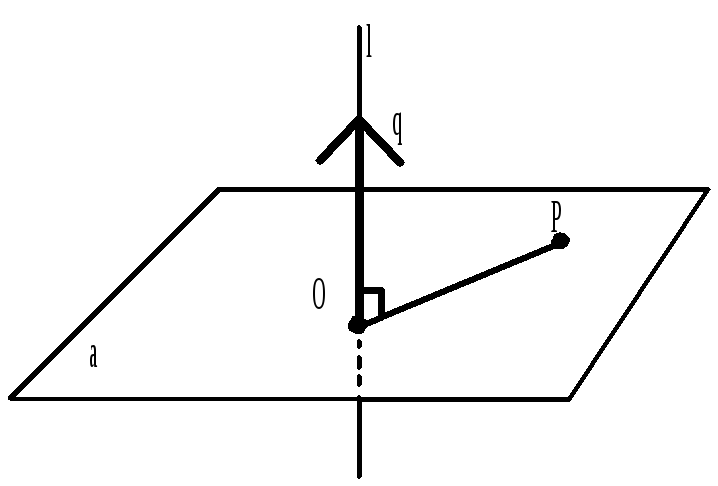Прямой l.

q = (3;-4;0) – направляющий вектор прямой l.

Так как α  l, то α  q, тогда q – нормальный вектор пл – ти α.

N_α = q = (3;-4;0)

Пл-ть α проходит через т. Р (1;2;0), значит, ее уравнение имеет вид:

3 (x-1)-4(y-2)+0(z-0);

α: 3x-4y+5=0

O –точка пересечения прямой l и пл-ти α.

Запишем уравнение прямой l в параметрическом виде:

x = 3t+8

y = 4t+1

z=0

Находим координаты т. О:

x = 3t+8,

y = -4t+1,

z = 0,

3x-4y + 5=0;

9t +24 +16t –4 +5 =0;

25t + 25 =0

t = -1

x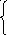 = -3+8=5

y = 4+1=5 O (5;5;0)

z = 0

OP- расстояние от т. Р до прямой l:

OP = √ (x_p – x₀)² + (y_p - y₀)² + (z_p-z₀)² = √ (1-5)² + (2-5)² + (0-0)² = 5 ед.

5.(925). Найти длину отрезка, отсекаемого от оси ординат плоскостью, которая проходит через точку А(1,1,6) перпендикулярно вектору АВ, где В – точка пересечения медиан треугольника, вершины которого совпадают с точками пересечения осей координат с плоскостью 12х+6у +z –24=0.

B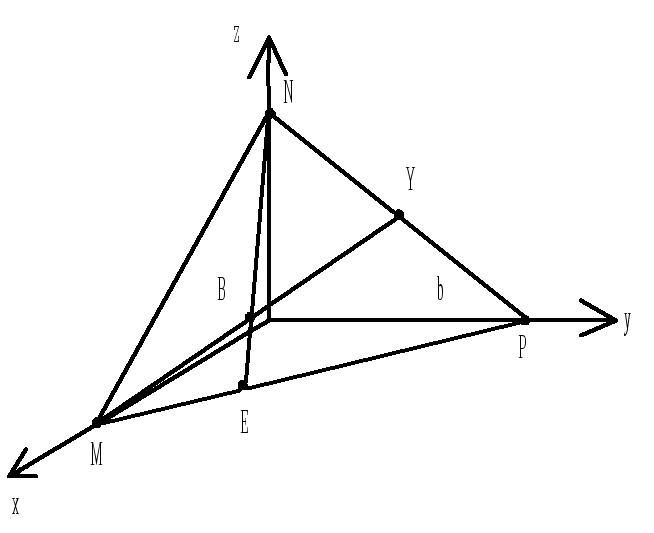 = 12 x +6y +z –24=0

M (2;0;0)

N (0;0;24)

P (0;4;0)

E – середина МР, тогда

x_M +x_P 2+0

x_E = = = 1

^{2 2}

y_M + y_P 0+4

y_E = = = 2 E(1;2;0)

^{2 2}

z_M + z_P 0+0 z_E = = = 0

^{2 2}

Y – середина NP:

x_N + x_P 0+0

x_Y = = = 0

^{2 2}

y_N + y_P 0+4

y_Y = = = 2 Y (0;2;12)

^{2 2}

z_{N +}+ z _P 24+0

z_Y = = = 12

^{2 2}

Уравнение прямой NE:

x- x_N = y – y_N = z - z_{N ,}

x_E –x_N y_E –y_N z _E – z_N

x-0 = y-0 = z-24

1-0 2-0 0-24

x y z-24

NE: = =

^{1 2 -24}

Уравнение прямой MY:

x-x_M = y-y_M = z - z_M

x_Y – x_M y_Y – y_M z_Y - z_M

x-2 = y –0 = z-0 ;

0-2 2-0 12-0

x-2 y z x-2 y z

MY: = = или = =

^{-2 2 12 -1 1 6}

Находим координаты т. В:

Запишем уравнение прямой MY в параметр. виде:

x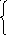 = - t +2

y = t

z = 6t

В точке пересечения прямых NE и MY, значит, ее координаты найдем, решив систему:

x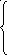 = -t +2,

y = t,

z = 6t,

x = y = z-24 .

1 2 -24

-t+2 = t

1. 2

-2t + 4 = t

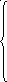4 4 2

t = . Тогда x = - + 2 =

^{3 3 3}

4

y =

³

z = 8

В 2; 4; 8

^{3 3}

2 4 1 1

AB = -1; -1; 8-6 = - ; ; 2

^{3 3 3 3} 1 1

Пл-ть α проходит через т. А (1;1;6) перпендикулярно вектору АВ = ; ; 2 ,

^{-3 3}

значит, ее уравнение имеет вид:

1 1

- (х+1) + (у-1) + 2 (z-6) = 0

^{3 3}

-x + 1 + y – 1 + 6z - 36=0;

α = -x + y + 6z –36 =0.

Точка пересечения пл-ти α с осью ординат:

x = z= o : y - 36 = 0, y = 36

Ответ : 36.

6. (512). Две прямые параллельны плоскости 4x+3y+6z = 0. Первая прямая проходит через точку Р (1,2,3) и пересекает ось абсцисс, а вторая – проходит через точку Q (3,0,0)и пересекает ось ординат. Найти косинус острого угла между направляющими векторами этих прямых.

α: 4x +3y +6z =0

P (1;2;3) є l₁ ; так как прямая l₁ пересекает ось абсцисс, то она проходит через точку A (a;0;0); l₁ α.

Q (3;0;0) є l₂; так как прямая l_{2 ПЕРЕСЕКАЕТ ОСЬ ОРДИНАТ, ТО ОНА ПРОХОДИТ ЧЕРЕЗ ТОЧКУ}

B (0;b;0); l₂ || l

AP = q₁ – направляющий вектор прямой l₂:

q₂ = (1-a; 2-0;3-0) = (3; - b;0)

N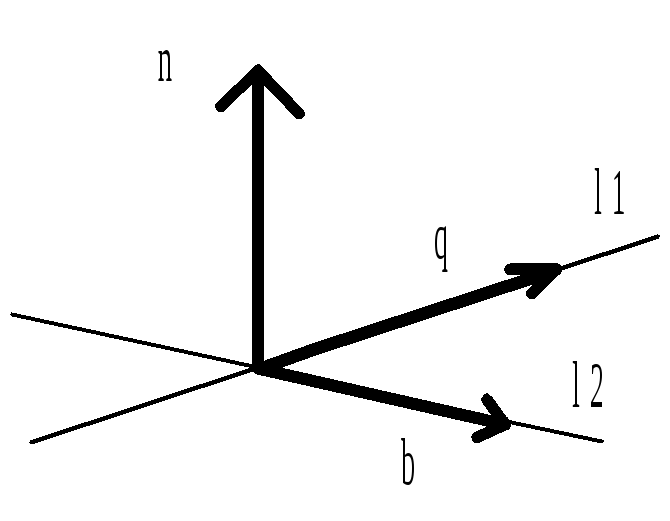α = (4;3;6) – нормальный вектор пл-ти α

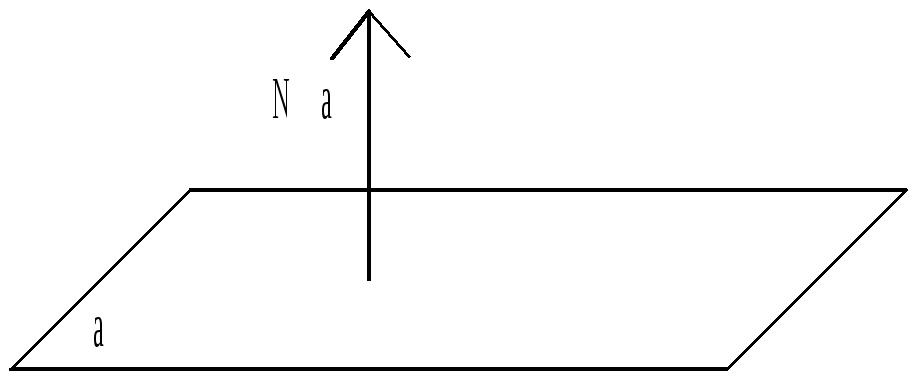
Так как l₁ || l и l₂ || l, то n || N_α, где n = q₂ * q₁

i j k

n = 3 -b 0 = -3bi – 9j + (6+b(1-a))k

1-a 2 3

Так как n || N₂, то соответствующие координаты этих векторов пропорциональны.

-3b = -9 = 6+b(1-a)

4 3 6

-3b = -9 6+4 (1-a) = -9

4 3 6 3

3b = 3 3+2+2a = -9

4 3 3

b = 4 2a = 14, a = 7.

Тогда q₁ = (-6;2;3) q₂ = (3;-4;0)

q₁ * q₂ -6*3+2(-4)+3*0 -26 26

cos (q_1,^q₂) = = = = -

q₁ * q₂ √ ( -6)² + 2² + 3² * √ 3² + (-4)² +0 7*5 35

26

Тогда косинус острого угла равен

35

7(С93.Б7). Найти координаты центра С (х_0,у₀) окружности радиусом 5, касающей прямой 3х+4у-6=0 в точке М (2,0), если известно, что точка С расположена в первой четверти.

l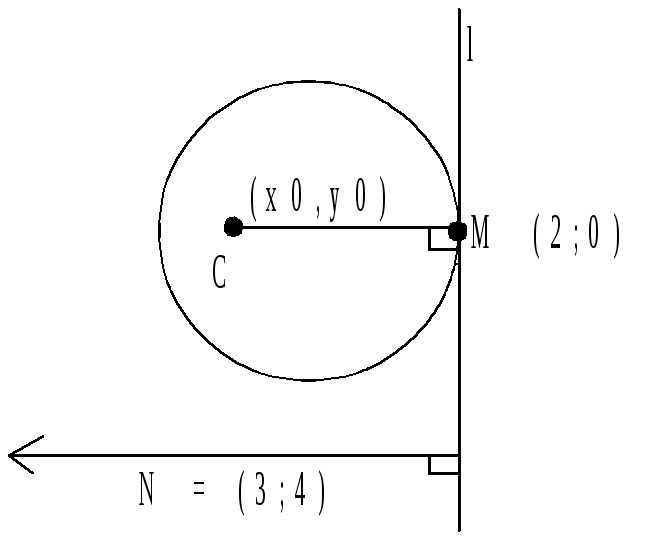: 3x+4y-6 = 0

Так как l – касательная, то СМ  l

СМ = (2-х₀; y₀)

N = (3;4)- нормальный вектор прямой l.

N  l, CM  l, значит, N || CM, тогда

2-x₀ = -y₀ , y₀ = 4(x₀ –2)

3 4 3

CM ² = 5²

CM ² = (2 – x₀)² + y₀² ;

4² (x₀-2)²

(2-x₀)² + =25; 32

16

(x₀ – 2)² + (x₀ – 2)² = 25;

9

25

(x₀ – 2)² * = 25;

9

(x₀ – 2)² = 9;

(x₀ – 2) = 3 , так как x₀ > 0 по условию задачи, то

x₀ – 2 = 3; 4(5-2)

x₀ = 5, тогда y₀ = = 4.

3

Ответ: С (5;4)

8. Дана кривая 9х² – 4у² – 18х + 56у – 223 = 0.

8.1. Доказать, что это кривая – гипербола.

8.2 (223.РП). Найти координаты её центра симметрии.

8.3(9С3.Р7).Найти действительную и мнимую полуоси.

8.4(893.РП). Записать уравнение фокальной оси.

8.5.Построить данную гиперболу.

9х² – 4у² – 18х + 56у – 223 = 0.

9(х² –2х+1) – 9 – 4(у² –14у +49 )+196 - 223 = 0

9( х –1)² – 4 (у –7)² = 36;

(х-1)² - ( у – 7)² =1 – каноническое уравнение гиперболы

2² 3²

(1;7) –центр симметрии

а =2- действ, полуось

в = 3 – мнимая полуось

у = 7 – уравнение фокальной оси.

9.Дана кривая х²⁺2х-2у+5=0.

9.1. Доказать, что данная кривая – парабола.

9.2(793.РП). Найти координаты её вершины.

9.3(323).Найти значение ее параметра р.

9.4(753.Б7). Записать уравнение ее оси симметрии.

9.5. Построить данную параболу.

х²⁺2х-2у+5=0;

( x + 1)² – 1 –2y + 5 = 0;

(x + 1)² = 2 (y-2) – каноническое уравнение параболы

(-1;2) – вершина параболы

p = 1>0 – ветви направлены вверх

x = -1 – ось симметрии

10.Дана кривая 8х² + 17у² + 12ху –28х –46у = 43.

10.1. Доказать, что это кривая – эллипс.

10.2 (803.РП). Найти координаты центра его симметрии.

10.3 (4Р3.РП). Найти его большую и малую полуоси.

10.4(433.БЛ). Записать общее уравнение фокальной оси.

10.5. Построить данную кривую.

8х² + 17у² + 12ху –28х –46у = 43.

Приводим квадратичную форму

В = 8х² + 17у² + 12ху к главным осям.

8 6

В =

6 17

Характеристическое уравнение матрицы В:

8 – λ 6

= 0

6 17- λ

( 8 – λ)(17 – λ) – 36 =0;

λ² + 25λ + 100 = 0;

D = 25

25 - 15 25 + 15

λ₁ = = 5, λ₂ = = 20 – собственные числа.

2 2

λ_1* λ₂ = 100>0, значит , заданная кривая – эллипс. Соответствующие собств. векторы:

1. λ₁ = 5 2) λ₂ = 20

(8-5) §₁ + 6§₂ = 0 (8 - 20) §₁ + 6§₂ = 0

§₁ + 2§₂ = 0 -2§₁ + §₂ = 0

(2;-1) (1;2)

Нормируем полученные собств. векторы и выбираем их за новый базис:

2 -1 1 2

i₁ = ; i₂ = ;

√5 √5 √5 √5

Матрица перехода Q от базиса О, i, j к базису Oi₁ j₁

2 1 2 _ 1

√5 √5 √5 √5

Q = Q^-1 = Q^T =

_ 1 2 1 2

√5 √5 √5 √5

Выражаем новые координаты через старые:

x₁ x 2x – y x +2y

= Q^T x₁ = y₁ =

y₁ y √5 √5

Уравнение эллипса в новой системе координат:

λ₁x₁² + λ₂y₁² + ax₁ + by₁ +C = 0 , где

(a;b) = (a₀₁, a₀₂) Q

a₀₁ = -28 , a₀₂ = -46

-28*2- 46 (-1) -28*1 - 46*2 -10 -120

(a;b) = ; = ;

√5 √5 √5 √5

10 120

5x₁² + 20y₁² - x₁ - y₁ = 43;

√5 √5

2 1 6 9

5 x₁² - x₁ + - 1 + 20 y₁² - y₁ + - 36 = 43