Контрольная работа 2 / 2- 1_Высшая математика_4

Министерство образования

Российской Федерации

ТОМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

СИСТЕМ УПРАВЛЕНИЯ И РАДИОЭЛЕКТРОНИКИ (ТУСУР)

ВОСТОЧНЫЕ СИСТЕМЫ

самосовершенствования

Контрольная Работа №2

по дисциплине Математика

Студент

Руководитель

Профессор кафедры КС,

д-р филос. наук

________ ________И.К. Сидоров

________

2003

Контрольная Работа по Математике №2

Вариант №1

1. М1 (-1,2), М2 (-3,-2)

Уравнение прямой, проходящей через две точки: М1 (x1,y1) и M2 (x2, y2) имеет вид:

Y - y1 = x - x1 имеет: y – 2 = x + 1 или y-2 = x+1 от куда

y2 -y1 x2 – x1 - 2- 2 -3 +1 -4 -2

y-2=2(x+1) , y= 2x+4. Уравнение прямой с угловым коэффициентом имеет вид:

y = kx + b

в нашем случае параметры k = 2; b = 4.

2. (М1) 5x – 12y – 65= 0, (М2) 5x – 12y +26=0

Так как начало координат лежит между этими прямыми (см рис №1), то найдем

расстояние от точки О (0,0) до прямых.

d

d1 = |5*0-12*0-65| = 65 =5

25+144 13

d

d1 O d2 d2= |5*0 – 12*0 +26| = 26= 2

25+144 13

и тогда d=d1+ d2=7 , а это есть сторона квадрата, тогда его площадь равна 49.

рис.1

3. P (-3, 2, 5) 4x + y – 3z + 13 = 0 x –2y + z – 11 = 0

Общее уравнение плоскости имеет вид ax + by + cz + d = 0

Запишем вектора нормали для плоскости: n1 (4, 1, -3) n2 (1, -2, 1)

Тогда уравнение плоскости запишем как условие компланарности

x+1 y-2 z-5

4 1 -3 = 0

1 -2 1

Разложим определитель по элементам первой строки

( x+3) * 1 -3 - ( y - 2) * 4 -3 + (z-5) * 4 1 = 0

-2 1 1 1 1 -2

( x+3)(1-6) – (y-2)(4+3) + (z-5)(-8-1)=0

-5x –15 –7y+14 –9z + 45 = 0

-5x – 7y –9z + 44= 0 или окончательно

5x + 7z + 9z – 44 = 0

4. l (0,3,4) 2x+y-z-6=0 2x+y-z-4=0

P1

M1

l

P2 M2

Уравнение прямой параллельной вектору l и проходящей через точку М0 (x0,y0,z0) имеет вид: (x-x0)/0= (y-y0)/3= (z-z0)/4

В качестве точки возьмем начало координат О(0,0,0) . Получим: x/0 = y/3 = z/4

Заменим это уравнение в параметрическом виде:

x = 0

x/0= y/3 = z/4=t откуда y = 3t

z = 4t

Подставим их в уравнение первой плоскости, находим параметр t.

2*0 + 3t – 4t –6 = 0, t=6

Для второй плоскости: 2*0 + 3t – 4t –4 =0, t=4

Отсюда находим точки М1 и М2, лежащие на плоскостях в точках пересечения с прямой

М1 (0, 18, 24) и М2 (0, 12, 16), а длина отрезка М1М2 равна:

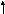
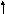
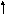
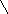
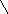
|M1M2| = (0-0) 2 + (12-16) 2 + (16-24) 2 = 0 + 36 + 64 = 10

5.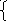

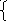(x-1)/m = (y-2)/n= z/34 1) 3x- 2y+ 3=0 2) 2x – 3z – 4= 0

y- 3z + 3= 0 y – 2z +1 = 0

Для прямых 1) и 2) найдем направляющие вектора. Так как они перпендикулярны нормальным векторам плоскости, то для прямой 1) имеем

i j k

l1 = N1* N2 = 3 –2 0 = i -2 0 - j 3 0 + k 3 -2 = 6 i + 9 j +3 k

0 1 -3 1 -3 0 -3 0 1

Для второй прямой:

i j k

l 2 = N1 * N2 = 2 0 -3 = i 0 -3 - j 2 -3 + k 2 0 = 3 i +4 j + 2 k

0 1 -2 1 -2 0 -2 0 1

Условие пересечения запишем в виде: x2-x1 y2-y1 z2-z1

l1 m1 n1 = 0

l2 m2 n2

Н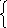айдем точку, через которую проходит прямая 1). Возьмем точку пересечения с координатной плоскостью yoz. Предположим x = 0, получим из системы

3x – 2y + 3 = 0

y – 3z + 3 = 0 тогда y = 3/2, z = 3/2, т. е. точка М1 (0, 3/2, 3/2)

Найдем точку М2 на прямой 2). Предположив x =0, находим из системы

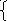2x - 3z – 4 =0

y – 2z + 1 =0 z = - 4/3 ; y = - 11/3, т.е. M2 (0, -11/3, - 4/3)

Из условия пересечения прямой (x-1)/m = (y-2)/n= z/34 с прямой 1) получим

0 – 1 3/2 – 2 3/2 – 0

6 9 3 = 0

m n 34

C прямой 2) получим:

0 – 1 - 11/3 – 2 - 4/3 – 0

3 4 2 = 0

m n 34

Раскроем эти определители и получим систему уравнений для определения параметров m и n.

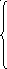
- 1 9 3 + 1 6 3 + 3 6 9 = 0

n 34 2 m 34 2 m n

- 1 4 2 + 17 3 2 - 4 3 4 = 0

n 34 3 m 34 3 m n

Или окончательно имеем систему:

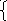
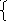12n – 15m = 204 или 4n – 5m = 66

- 2n – 6m = -442 n – 3m = 221

Отсюда находим m = - 204, n = 664, т.е. при m = - 204, n = 664 прямая пересекается с прямыми 1) и 2).

6.

Найдем проекцию точки М0 (0,0, z0) на плоскость 2x + 3y + 6z + 7 = 0 . Через М0 проведем перпендикуляр (x – 0)/2 = ( y – 0)/3 = (z – z0)/6, который пересекает плоскость в точке М1 . Найдем ее координаты.

Из уравнения прямой находим x = 2t

y = 3t

z = 6t + z0

и подставим в уравнение плоскости

4t + 9t + 36t + 6z0 + 7 = 0

откуда t = - ( 6z0 + 7)/ 49. Точка М1 должна лежать и на прямой, поэтому ее координаты

М1 - (12z0 + 14)/49, - ( 18z0 + 21)/49, - ( 36z0 + 42)/49 +z0

По условию задачи |M0M1| = 7

Имеем: (- (12z0 + 14)/49) 2+ (- ( 18z0 + 21)/49) 2 +(- ( 36z0 + 42)/49) 2 = 49

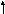
Или 3(z0) 2 + 7z0 – 196 = 0

Найдем корни z01 = - 56/6, z02 = 7. Так как по условию задачи z0> 0 , то берем z0 = 7.

И координаты точки М1 ( -2, -3, 1)

Напишем уравнение плоскости, проходящей через точку М0 (0,0,7) и параллельной плоскости 2x + 3y + 6z +7 =0

Запишем уравнение связки плоскостей, проходящей через точку М0.

2(x – 0) + 3( y – 0) +6(z – 7) =0 или 2x + 3y + 6z – 42 =0

Точка пересечения находится как точка пересечения плоскости 2x + 3y + 6z – 42 = 0 с осью Ox. Положим y =0, z =0, находим 2x – 42 = 0

X0 = 21. Это абсцисса точки пересечения прямой с осью аббсцисс.

7.

x 2 + y 2 – 4x + 6y =17 , M(1,2)

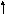
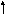
П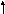риведем уравнение окружности к каноническому виду. Для этого в левой части выделим полные квадраты.

(x 2 – 4x + 4) + ( y 2 + 6y +16) – 4 – 16 = 17 или (x - 2) 2 + (y + 4) 2= 37

Л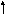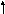егко проверить, что точка М(1,2) лежит на окружности. Для этого подставим ее координаты в уравнение окружности.

( 1 – 2) 2 + (2 + 4) 2 = 37

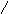
Это окружность с R = 37 и центром в точке О (2, -4)

Напишем уравнение радиуса ОМ.

Y – 2 = x – 1 или y –2 = x – 1 , откуда

-4 –2 2 – 1 - 6 1

y = -6x + 8. Так как касательная в точке М перпендикулярна радиусу ОМ, то ее угловой коэффициент k = - 1/-6 = 1/6, а тогда уравнение касательной будет иметь вид:

y – 2 = 1/6( x – 1) или y = x/6 + 11/6

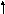
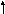
8. 9x 2 + 25y - 18x – 150y + 9 = 0

8.1.Выделим полный квадрат переменных

9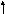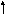( x 2 – 2x + 1) – 9 + 25( y 2 – 6y + 9) – 225 + 9 =0 или

9( x – 1) 2 + 25 ( y – 3) 2 = 225. Разделим обе части на 225. Получим

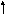
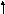
(x - 1) 2 + ( y – 3) 2 = 1

25. 9

Отсюда видно, что это уравнение Эллипс

2. Центр симметрии О(1,3)

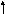
3. Б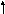ольшая полуось a = 5, меньшая полуось b = 3.

4. Найдем c = a 2 – b 2 = 25 – 9 = 4

Поэтому фокусы эллипса F1(5;3) и F2( -4;3) Уравнение фокальной оси y = 3

8.5.

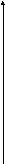
y

F2 F2 3 O F1

-4 0 1 5 x

9. x 2 – 10x + 2y + 25 = 0

Выделим полный квадрат переменной x

Имеем (x - 10x +25) + 2y=0

y = - ½(x – 5) 2

Это уравнение параболы с вершиной а точке О(5;0). Ветви ее направлены вниз. Ось симметрии x =5. Для нахождения параметра p уравнение должно иметь вид:

x 2 = 2py

В нашем случае (x – 5) 2 = -2y, тогда 2p= -2, p = -1.

Построим данную прямую.

X =1;y =-8 Y

X=7;y=-2

X=3;y=-2

0 5 x

1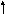0. 15x 2 –20xy – 70x +20y +135 = 0

Приведем квадратичную форму b = 15x 2 – 20xy к главным осям. Ее матрица

B = 15 -10

-10 0

Запишем характеристическое уравнение этой матрицы 15 – n -10 = 0

-10 0 – n

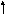
- n(15 – n) – 100 = 0 или n 2 + 15n +100 = 0

Найдем корни n1= 20, n2 = -5. Так как n1*n2< 0 то кривая – гипербола.

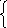
Определим собственные вектора. При n = 20 получим систему -5t1 – 10t2 = 0

- 10t1 – 20t2 =0

Отсюда получаем t1 = - 2t2. в качестве первого базисного вектора примем

i 1 = ( - 2/ 5 ; 1/ 5 )

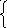
При n = -5 получим систему 20t1 – 10t2 = 0 отсюда t2=2t1. В качестве второго ба

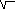
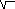-10t1 + 5t2 = 0 зисного вектора примем

j = (1/ 5 , 2/ 5 )

Перейдем от координат (x,y) к новым (x1,y1) по формулам

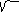
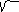
X1 = (-2x + 4)/ 5 , y1 = x =24/ 5

Уравнение приведется к виду:

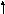
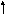
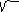
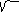
20x 2 – 5y 2 + 160x/ 5 - 30y/ 5 +135 = 0

Выделив полный квадрат переменных, получим

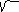
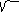
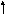
20( x – 4/ 5 ) 2 - 5 ( y + 3/ 5 ) 2 + 80 = 0 Разделим на -80

Получим:

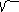
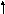
(x – 4/ 5 ) 2 + ( y + 3/ 5 ) 2 = 1 или

- 4 16

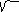
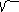
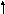
(y + 3/ 5 ) 2 - ( x – 4/ 5 ) 2 = 1

16. 4

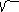
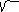
Это уравнение гиперболы с центром симметрии в точке О ( 4/ 5 ; - 3/ 5 )

С полуосями a = 4, b = 2

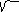
Y F1 ( 4 / 5 ; 17/ 5 )

x

O( 4/ 5 ; -3/ 5 )

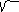
F2(4/ 5 ; - 20 / 5 )