Контрольная работа 2 / 2- 1_Высшая математика_6

Томский межвузовский центр дистанционного образования

Томский государственный университет

систем управления и радиоэлектроники (ТУСУР)

Кафедра промышленной электроники (ПрЭ)

Контрольная работа № 2

по дисциплине «Высшая математика»

(Учебное пособие «Высшая математика»,

авторы: Магазинников Л. И., Магазинникова А. Л. 2003г)

1. Запишите уравнение прямой, проходящей через точки М₁(-1,2) и М₂(-3,-2). Найдите значение параметров k и b для этой прямой.

РЕШЕНИЕ:

1) Уравнение прямой в общем виде: y = kx + b; Подставим значения точки М1:

-k + b = 2 и точки М2 : -3k + b= -2.

2)Составляем систему из полученных выше уравнений и находим параметры k и b :

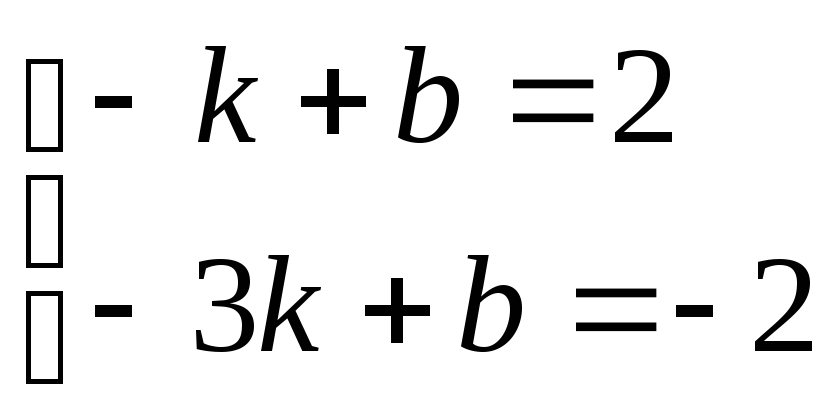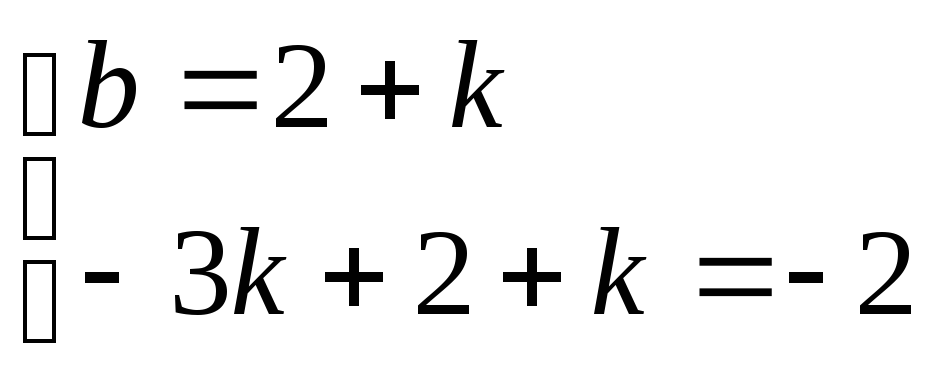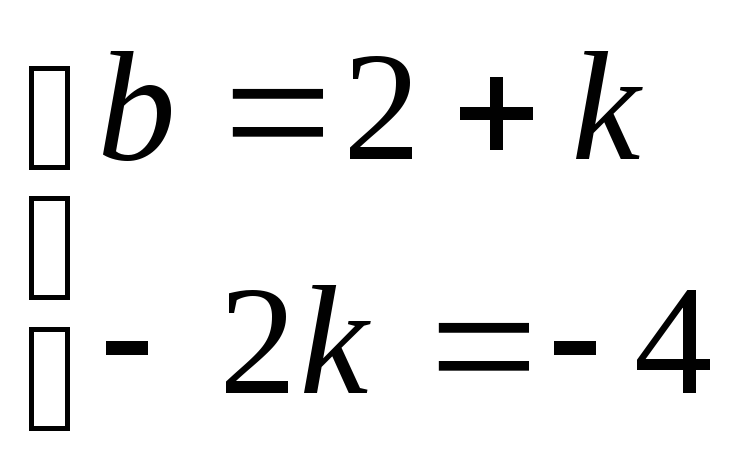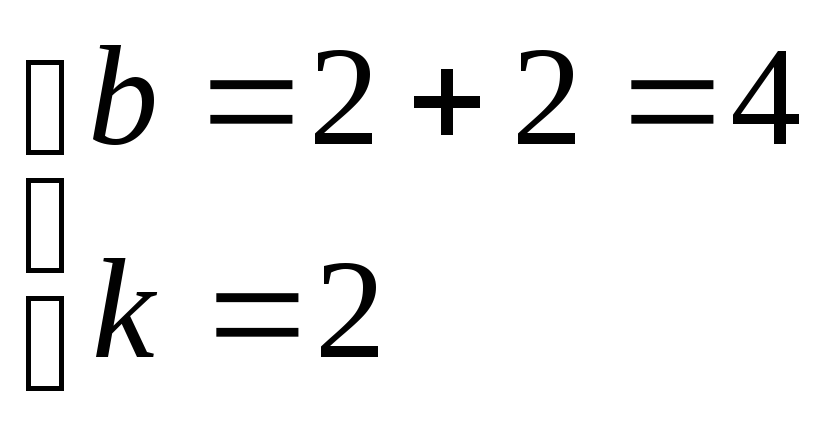; ; ; ; => y=2x+4 .

ОТВЕТ: k = 2 ; b = 4.

2. Две стороны квадрата лежат на прямых 5x - 12y – 65 = 0 и

5x - 12y + 26 = 0.Вычислить его площадь.

РЕШЕНИЕ:

1)= , где а – сторона квадрата.

2)Пусть L1= 5x - 12y – 65 = 0, а L2= 5x - 12y + 26 = 0; L1 ll L2 (т.к. А1=А2=5, В1=В2=-12 [A1/A2=B1/B2] ) =>, что а = расстоянию между L1 и L2 .

3) Пусть M - произвольная точка прямой L1, тогда

M. У L2

a будет равно расстоянию от точки M до прямой L2 => Х

a , где , тогда : а М L1

a = 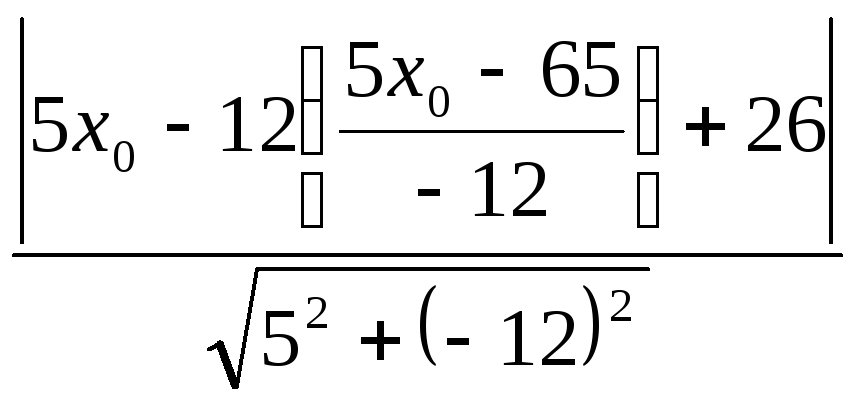= ( ед.)

4)из п.3=> (кв.ед.)

ОТВЕТ: кв.ед.

3. Запишите общее уравнение плоскости, проходящей через перпендикуляры, опущенные из точки P(-3,2,5) на плоскости

4x + y – 3z + 13 = 0 и x – 2y + z – 11 = 0.

РЕШЕНИЕ:

1)Пусть плоскость а = ;плоскость b=, а

полскость w-искомая;

Р(-3,2,5) принадлежит w

2)N1a; N2b т.е. N1(4,1,-3); N2(1,-2,1)

Плоскость w параллельна N1 и N2 (по условию).

. N=(N1*N2)=

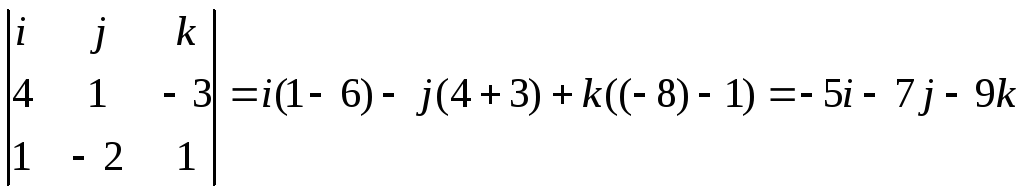
3)Т.к. w параллельна N1 и N2 , => Nw и проходит через точку P(-3,2,5), тогда

w=-5(x-(-3))-7(y-2)-9(z-5)=0:

-5(x-(-3))-7(y-2)-9(z-5) =0;

-5x-15-7y+14-9z+45=0;

-5x-7y-9z-15+14+45=0;

-5x-7y-9z+44=0 => w= -5x -7y -9z +44 =0

ОТВЕТ: -5x-7y-9z+44=0 – искомое уравнение

4. Найдите длину отрезка прямой, параллельной вектору l = (0,3,4), между точками пересечения её с плоскостями 2x + y – z – 6 = 0 и

2x + y – z – 4 = 0.

РЕШЕНИЕ:

1)Пусть k – прямая параллельная вектору l(0,3,4); a = 2x+y-z-6 = 0,а b= 2x+y-z-4=0, тогда

ka=A;kb=B. => длина искомого отрезка и есть длина АВ

2)Пусть М - произвольная точка принадлежащая k

Уравнение прямой k, проходящей через точку :

k = ; .

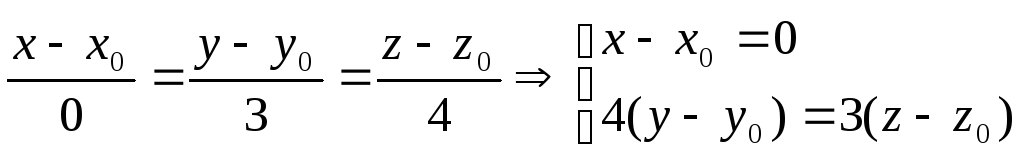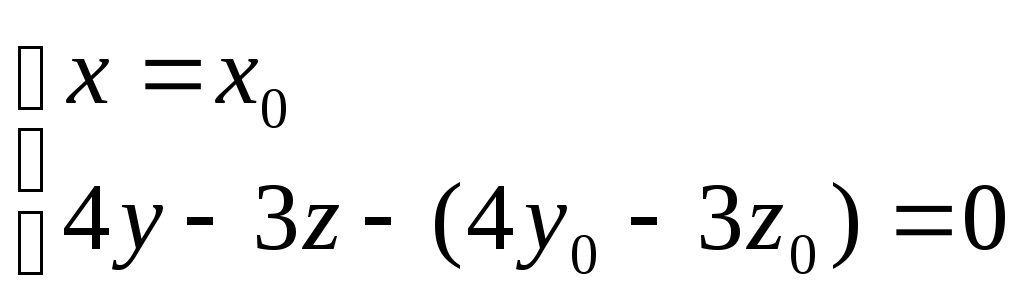3)Найдем координаты точки A:

; ;

.

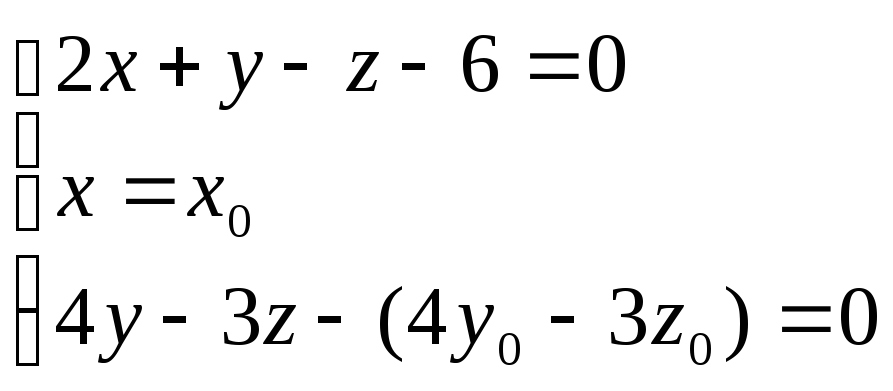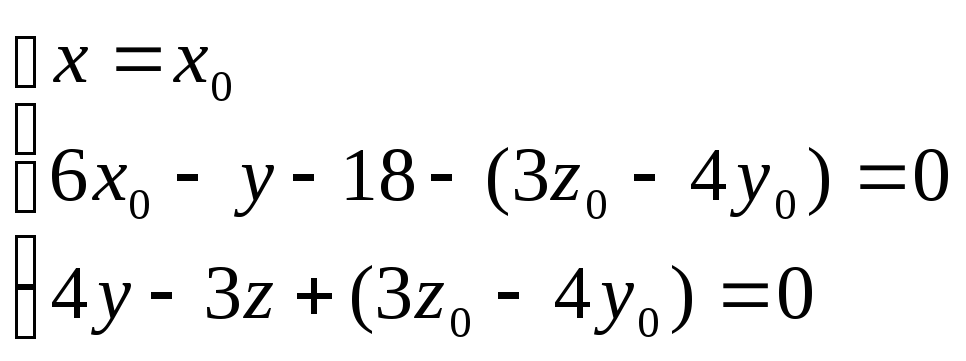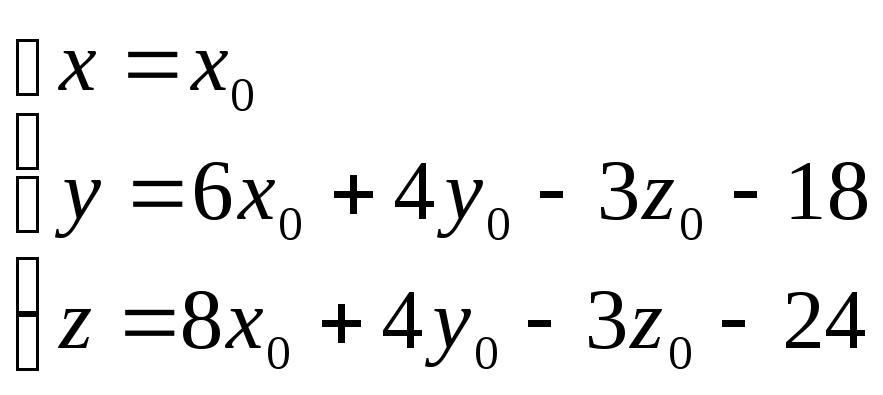4)Найдем координаты точки B:

; ;

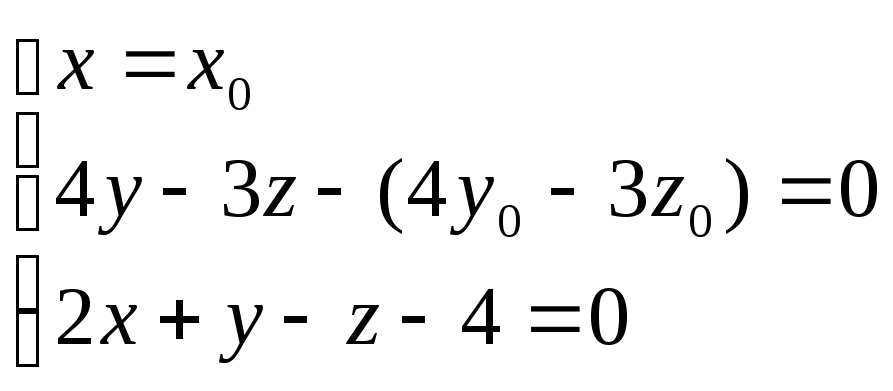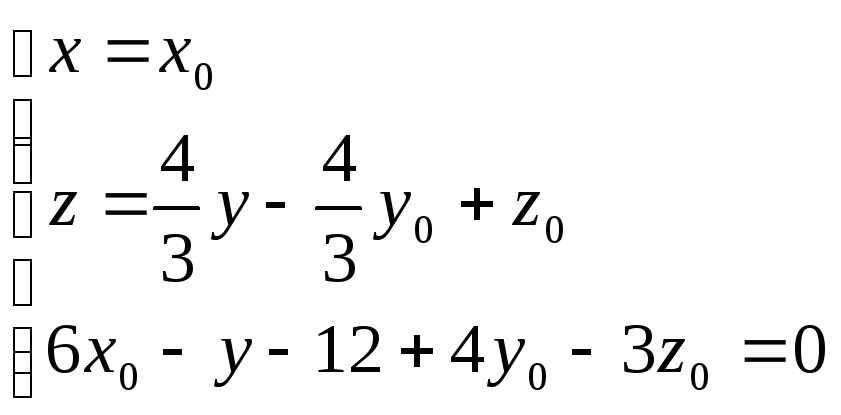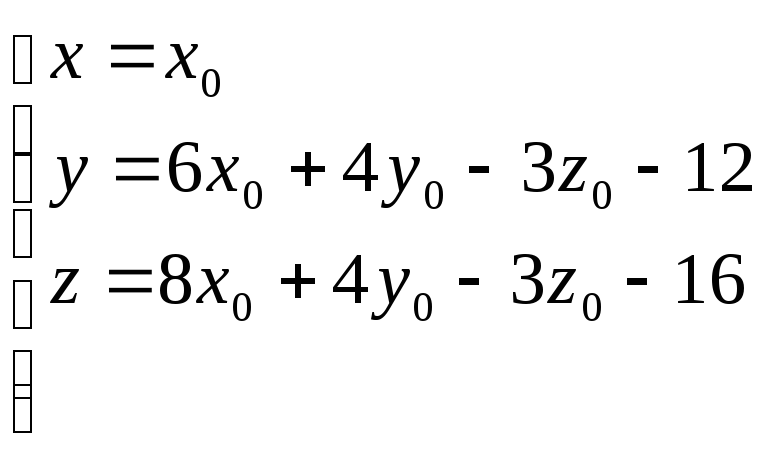. => (ед.)

ОТВЕТ: длина отрезка = 10 ед.

5. Найдите те значения m и n, при которых прямая пересекает прямые

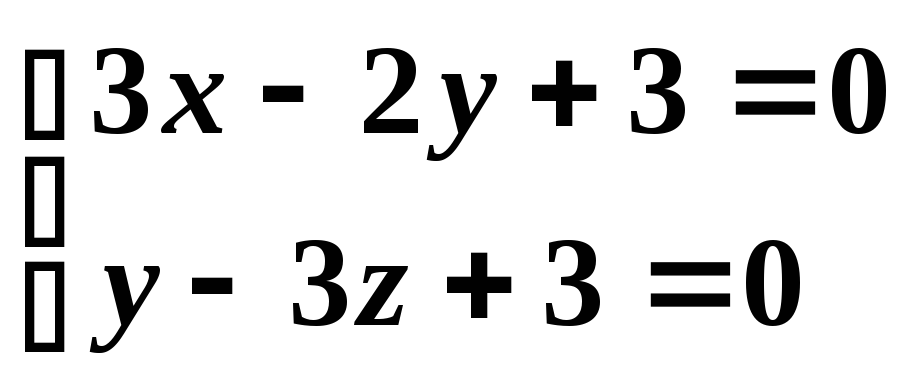и .

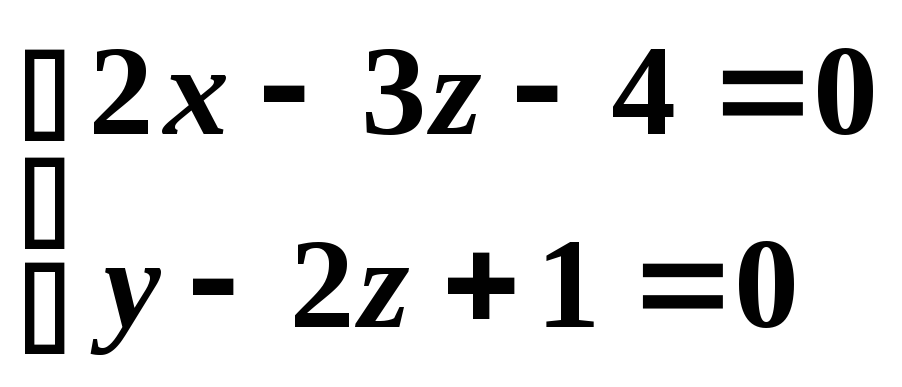РЕШЕНИЕ:

1)Пусть ; ; ;

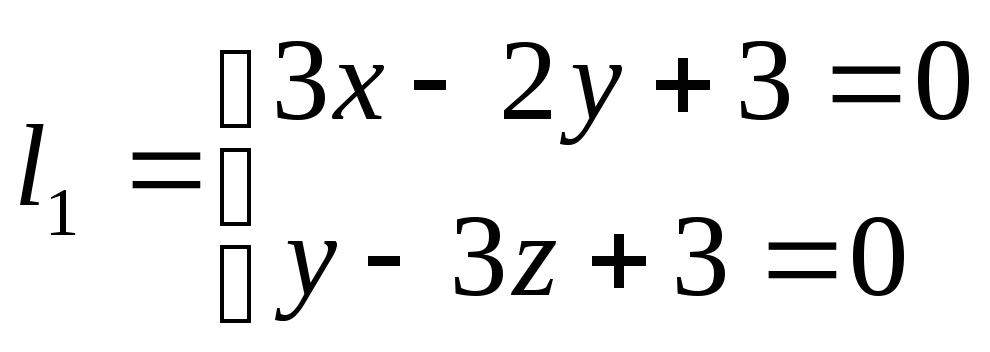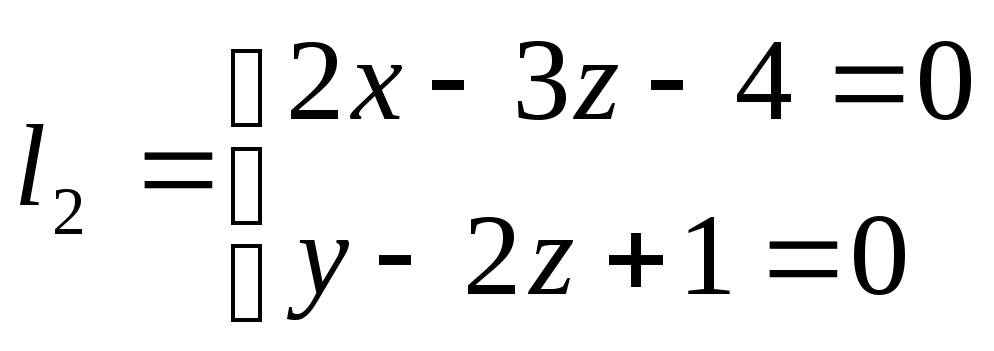2)Записываем уравнения данных прямых в векторной форме:

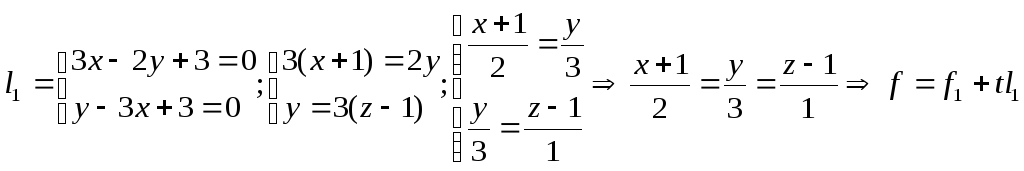, где

, где

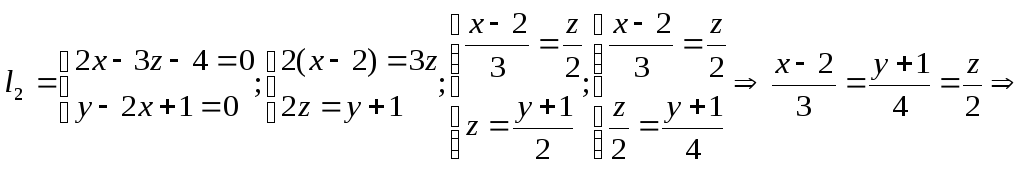
3)Прямые и пересекаются, если: ; (-2,-2,1)

прямые и пересекаются, если:(1,-3,0)

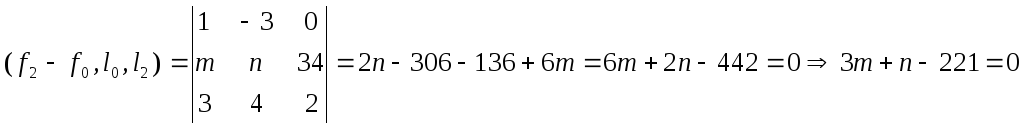
4)Находим m и n из системы уравнений:

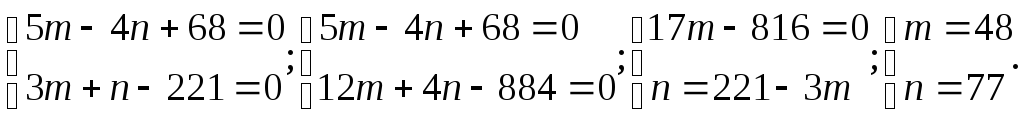
ОТВЕТ: m = 48, n = 77.

6. Дано, что прямая, пересекающая ось аппликат в точке , параллельна плоскости , отстоит от нее на расстоянии 7 и перпендикулярна оси ординат. Найдите абсциссу точки пересечения этой прямой с координатной плоскостью .

РЕШЕНИЕ:

1. Пусть l – прямая; M₀(0,0,z₀); плоскость a = 2x+3y+6z+7=0, d=7, М- искомая точка пересечения l с z=0

2. M₀ l и l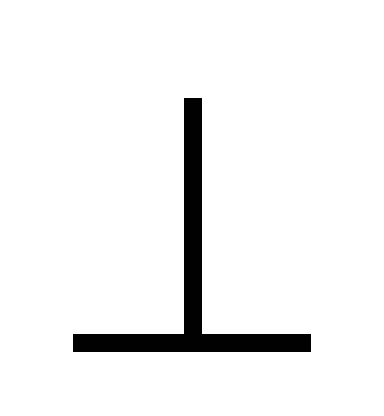 OY (по условью) , тогда уравнение прямой l равно:

(n=0 т.к. l OY)

3)Прямая l и вектор w (m,0,k) параллельны, т.к l a , то и w N(2,3,6)

4)Из п. 3 => N*w=2m+0+6k=0, т. е. m = -6k/2 = -3k => уравнение l равно:

;

5)Т.к. M₀ l, то расстояние от точки M ₀ до плоскости l=d=7 =>

Уравнение l равно :

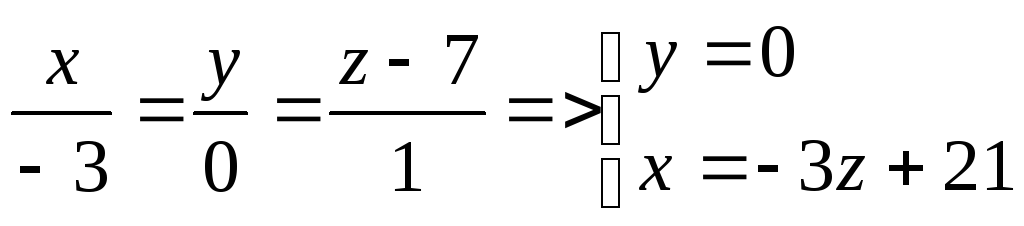
6)Найдем координаты точки М :

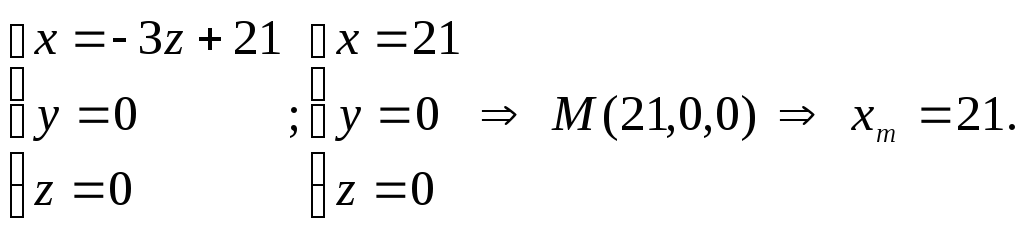
ОТВЕТ: 21

7. Запишите уравнение касательной к окружности

x²+y²-4x+8y=17 в точке М(1,2).

РЕШЕНИЕ:

1)Уравнение к окружности: (x-x₀)²+(y-y₀)²=R²:

2)Выделим полные квадраты:

x²+y²-4x+8y=17:

x²-2*2*x+4-4+y²+2*4*y+16-16=17;

(x-2)²-4+(y+4)²-16=17;

(x-2)² +(y+4)²=37

Центр данной окружности О (2,-4), радиус R=

3)Как известно. Касательная к окружности перпендикулярна радиусу, проведенному в точку касания. По этому вектор ОМ(-1,6) можно принять в качестве вектора нормали касательной, следовательно, уравнение касательной можно записать в виде –x+6y+C=0. Эта прямая проходит через точку М(1,2), т. е.

-1*1+6*2+С=0;

-1+12+С=0;

11+C=0;

С=-11 => уравнение касательной : -x+6y-11=0

ОТВЕТ: -x+6y-11=0

8. Дана кривая 9x²+25y²-18x-150y+9=0.

8.1 Докажите, что эта кривая - эллипс.

8.2Найдите координаты центра симметрии

8.3Нфйдите его большую и малую полуоси

8.4Запишите уравнение фокальной оси

8.5 Постройте данную кривую

РЕШЕНИЕ

8,1Выделяем полные квадраты:

9x²+25y²-18x-150y+9=0;

9*(x²-2*1*x+1)-9+25*(y²-2*3*y+9)-225+9=0;

9*(x-1)²+25*(y-3)²=225;

(x-1)²/25+(y-3)²/9=1

=> данная кривая эллипс.

8.2 Центр симметрии находится в точке (1,3).

8.3 Большая полуось: a = 5 ; . Малая полуось: b = 3

8.4 Уравнение фокальной оси: y = 3 .

8.5

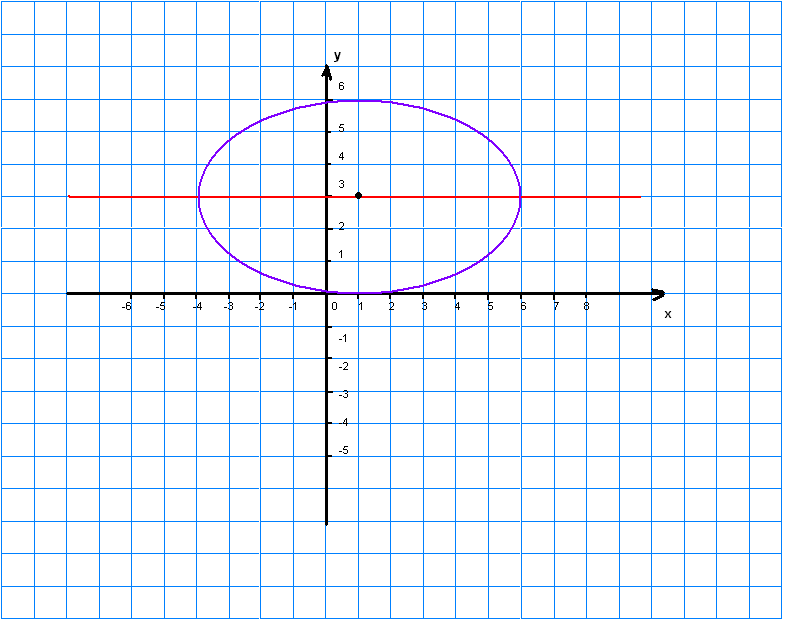
9. Дана кривая x²-10x+2y+25=0 .

9.1 Докажите, что эта кривая – парабола.

9.2Найдите координаты её вершины.

9.3Найдите значение её параметра p.

9.4Запишите уравнение её оси симметрии.

9.5Постройте данную пораболу.

РЕШЕНИЕ:

9.1Выделяем полный квадрат:

x²-10x+2y+25=0;

x²-2*5*x+25+2y=0;

(x-5)²=-2y;

y=(x-5)²/(-2) -данная кривая парабола

9.2. Координаты вершины (5,0)

9.3. Значение параметра:p= -1

9.4. Уравнение оси симметрии: x=5.

9.5.

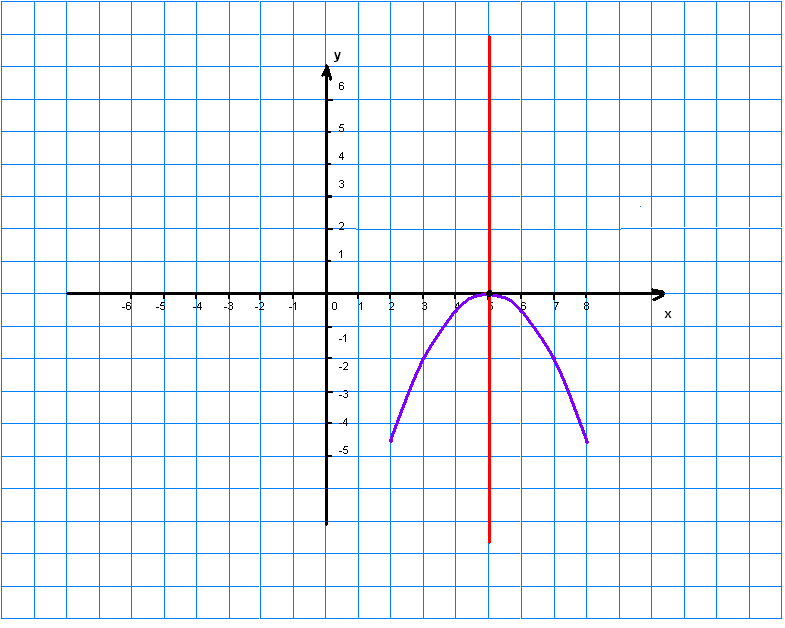
10. Дана кривая 15x²-20xy-70x+20y+135=0.

10.1 Докажите, что эта кривая – гипербола.

10.2Найдите координаты её центра симметрии.

10.3Найдите действительную и мнимую полуоси.

10.4Запишите общее уравнение фокальной оси.

10.5Постройте данную гиперболу.

РЕШЕНИЕ:

10.1

1) Для облегчения вычислений, все элементы данного уравнения можно сократить на 5:

15x²-20xy-70x+20y+135=0;

3x²-4xy-14x+4y+27=0

2).Квадратичную форму: В(x,y)=3*x²+2*(-2)*x*y-0*y² приводим к главным осям.

Для этого записываем матрицу этой квадратичной формы:

. Записываем и решаем характеристическое уравнение:

(собственные числа)

Т. к. собственные числа имеют разные знаки, то и данное уравнение определяет кривую гиперболического типа, т.е. данная кривая – гипербола.

10.2

Находим собственные векторы матрицы В:

Для .

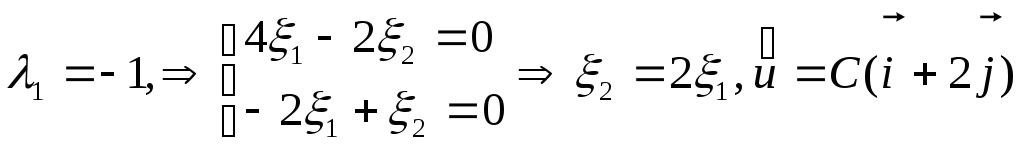Для .

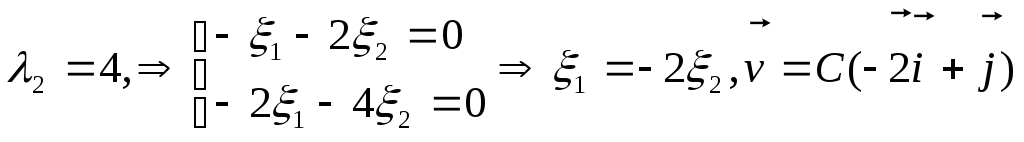Чтобы пронормировать примем

тогда векторы нового базиса:

Матрица перехода от базиса имеет вид

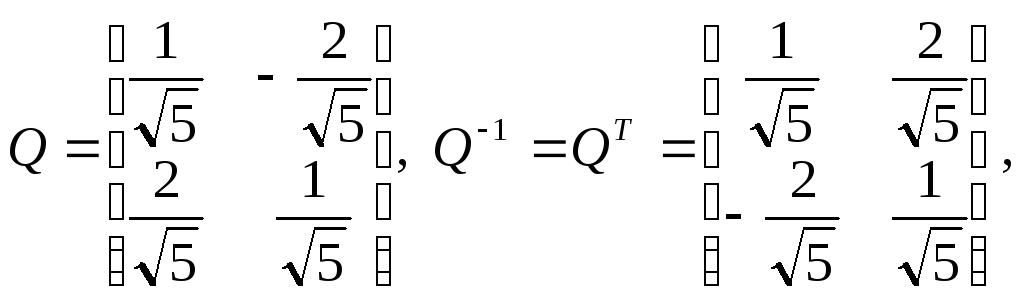
перейдем к новым координатам:

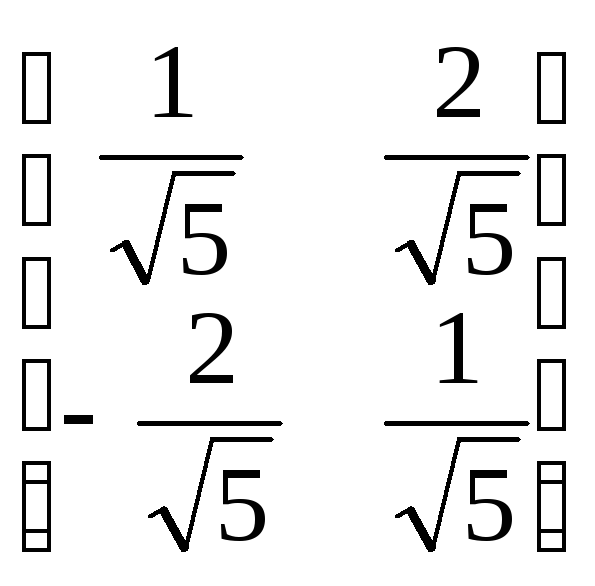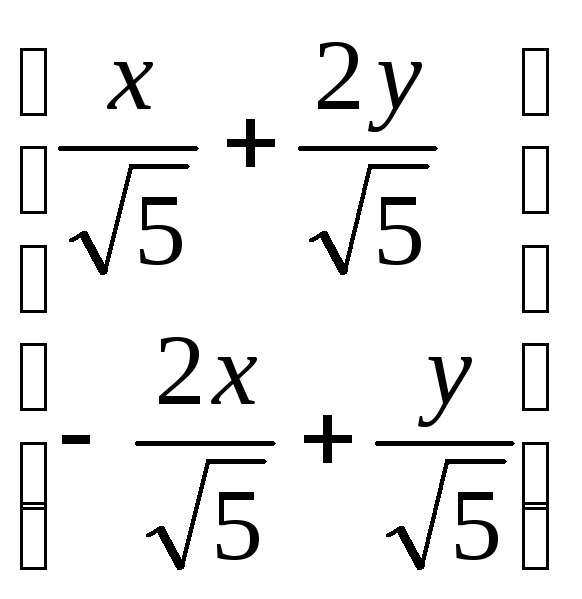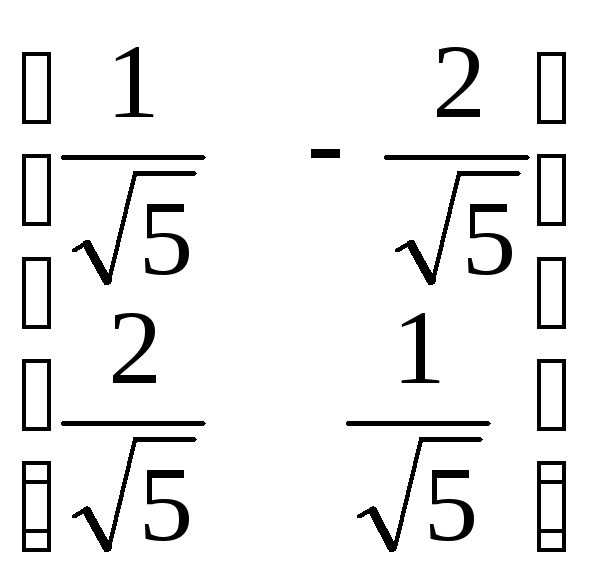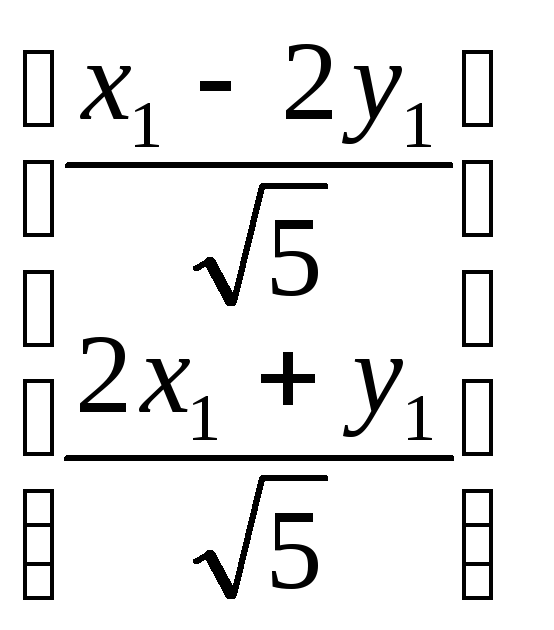=*= т.е.

= * = т.е.

Подставим выражение для x и y в первоначальное :

Перейдем к новым координатам:

т.е.

Тогда, уравнение гиперболы в системе координат O₁ X₂ Y₂: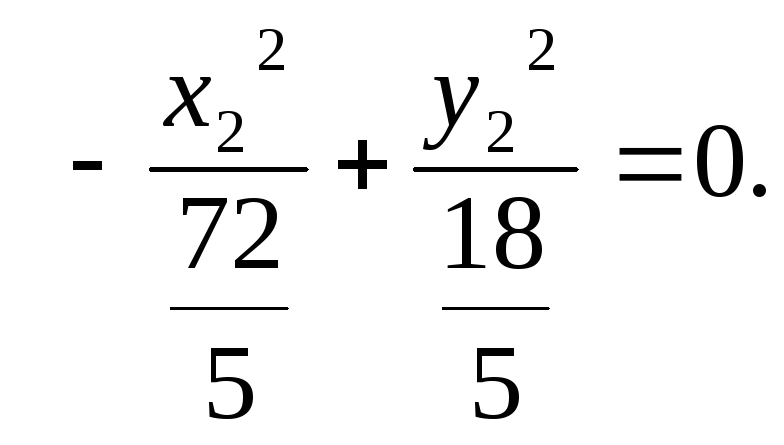

Уравнение оси O₁ X₁:x+2y+3=0, уравнение O₁Y₁ :2x-y-4=0

Координаты центра симметрии O₁ :

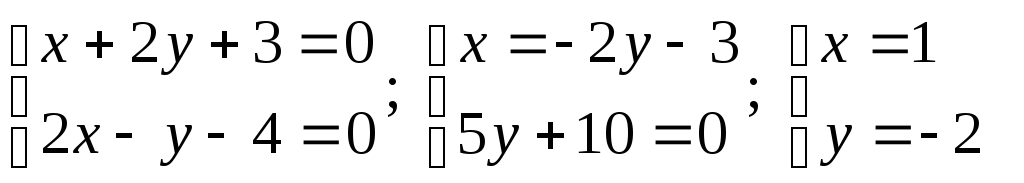=> O₁ (1,-2).

3. Действительная полуось:

Мнимая полуось:

3. Уравнение фокальной оси : 2x-y-4=0