Контрольная работа 2 / 2- 1_Высшая математика_5
.doc.
Высшая математика.
Контрольная работа № 2.
Вариант 1.
Задание 1.
Записать уравнение прямой, проходящей
точки
![]() и
и
![]() Найти значения параметров k
и b для этой прямой.
Найти значения параметров k
и b для этой прямой.
Решение.
Уравнение прямой, проходящей через
точки
![]() и
и
![]() имеет вид
имеет вид
![]() .
.
Значит
![]() или 4(х+1)=2(у-2)
или 4(х+1)=2(у-2)
У = 2х + 4, где k = 2; b = 4.
Задание 2.
Две стороны квадрата лежат на прямых 5х – 12у –65 = 0 и 5х – 12у + 26 = 0. Вычислить его площадь.
Решение.
Так как
![]() то прямые параллельны и они различны.
Найдем длину стороны квадрата - это
расстояние между параллельными
прямыми. Возьмем точку
то прямые параллельны и они различны.
Найдем длину стороны квадрата - это
расстояние между параллельными
прямыми. Возьмем точку
![]() первой прямой. Тогда расстояние от
точки
первой прямой. Тогда расстояние от
точки
![]() до второй прямой равно
до второй прямой равно
![]()
![]()
![]()
Значит
![]() .
Тогда
.
Тогда
![]()
Задание 3.
Записать общее уравнение плоскости,
проходящей через перпендикуляры,
опущенные из точки![]() на плоскости 4х + у –3z +
13 =0 и х –2у +z – 11 = 0.
на плоскости 4х + у –3z +
13 =0 и х –2у +z – 11 = 0.
Решение.
Запишем уравнение любой прямой,
проходящей через точку P:
![]() .
.
Координаты (
![]() направляющего вектора прямой,
перпендикулярной плоскости, можно
заменить координатами нормального
вектора n = (4; 1; -3) плоскости
4х + у – 3z + 13 =0. Тогда
уравнение прямой запишется в виде
направляющего вектора прямой,
перпендикулярной плоскости, можно
заменить координатами нормального
вектора n = (4; 1; -3) плоскости
4х + у – 3z + 13 =0. Тогда
уравнение прямой запишется в виде
![]()
Найдем проекцию точки P на данную плоскость, решив совместно уравнения
4х + у – 3z + 13 = 0,
![]()
Перепишем уравнение прямой в виде:
![]()
Подставляя эти выражения для x, y, z в уравнение плоскости найдем t.
4(4t – 3 ) + t + 2 – 3 (-3t + 5) + 13 = 0
16t –12 + t + 2 + 9t – 15 + 13 = 0
26t = 12, t =
![]()
Тогда
![]()
![]()
![]()
![]() проекция
точки P на плоскость
4x + y – 3z
+ 13 = 0.
проекция
точки P на плоскость
4x + y – 3z
+ 13 = 0.
Уравнение прямой, проходящей через
точки P и
![]() .
.
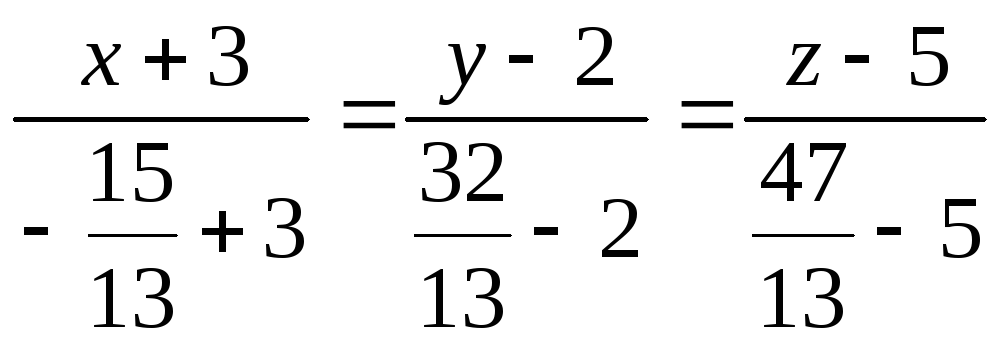
(1)
![]()
Теперь найдем проекцию точки P на плоскость x- 2y + z – 11 = 0.
![]()
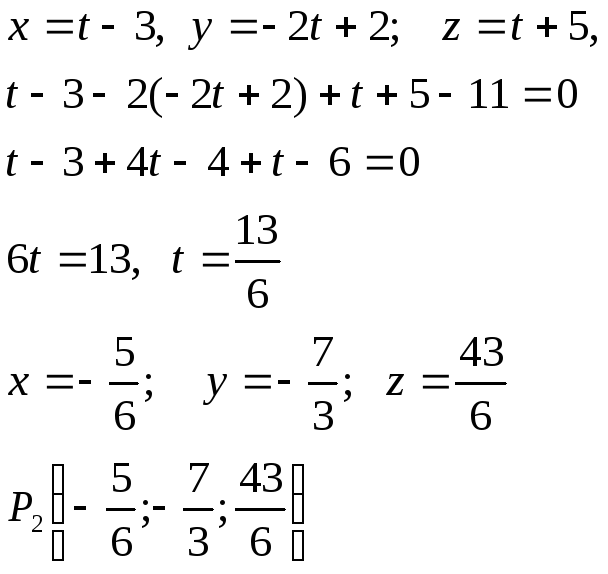
Уравнение прямой проходящей через
точки P и
![]() .
.
![]() (2)
(2)
Искомая плоскость проходит через
прямые (1) и (2). Так как величины
![]() не пропорциональны величинам
не пропорциональны величинам
![]() то прямые пересекаются при выполнении
условия
то прямые пересекаются при выполнении
условия
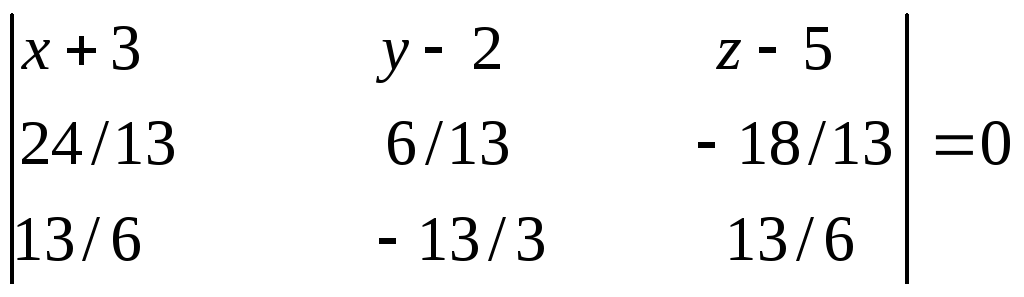

Задание 4.
Найти длину отрезка прямой, параллельной
вектору
![]() ,
между точками пересечения её с
плоскостями 2x + y
– z – 6 = 0 и 2x
+ y – z – 4 =
0.
,
между точками пересечения её с
плоскостями 2x + y
– z – 6 = 0 и 2x
+ y – z – 4 =
0.
Решение.
Плоскости параллельны, т.к.
![]()


![]()
![]()
![]() от точки
от точки
![]() плоскости
плоскости
![]() отложим вектор
отложим вектор










![]()
![]()
![]()
![]()
![]()
![]()
![]()





![]() А
А![]()
![]()

Отрезки параллельных прямых, заключенных
между параллельными плоскостями
равны. Значит длина искомого отрезка
равна длине вектора
![]() .
.
![]()
Ответ 5.
Задание 5.
Найти те значения m и
n, при которых прямая
![]() пересекает прямые
пересекает прямые
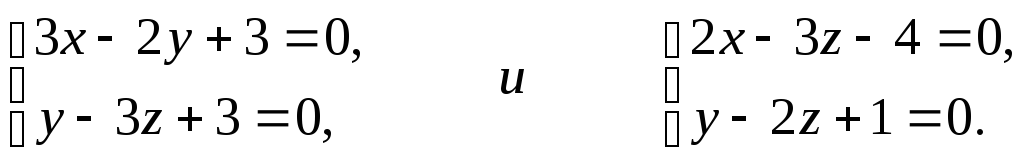
Решение.
Приведем уравнения (1) и (2) к каноническому виду.
(1)
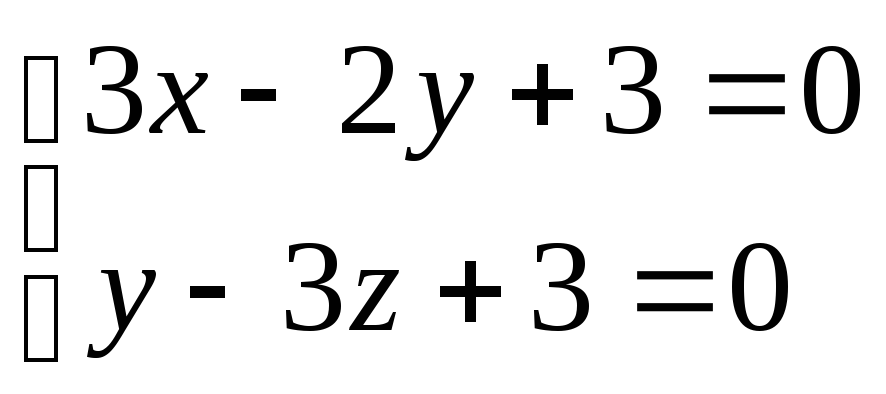
Найдем
![]()
![]() параллельный
искомой прямой. Так как он должен
быть перпендикулярен нормальным
векторам.
параллельный
искомой прямой. Так как он должен
быть перпендикулярен нормальным
векторам.
![]()
заданных плоскостей, то за S
можно принять векторное произведение
векторов
![]() .
.
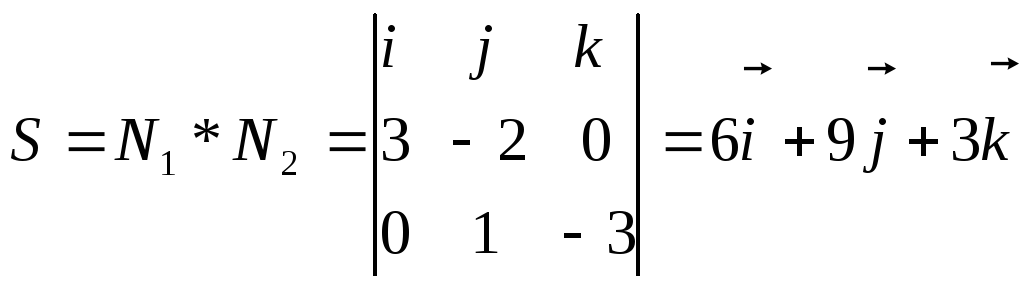
Таким образом
![]() в качестве точки
в качестве точки
![]() через которую проходит искомая
прямая, можно взять точку пересечения
и с любой из координатных плоскостей.
через которую проходит искомая
прямая, можно взять точку пересечения
и с любой из координатных плоскостей.
Например, с плоскостью XOZ.
Так как при этом
![]() то координаты
то координаты
![]() определяются из системы уравнений
заданных прямых, если в них положить
y = 0.
определяются из системы уравнений
заданных прямых, если в них положить
y = 0.
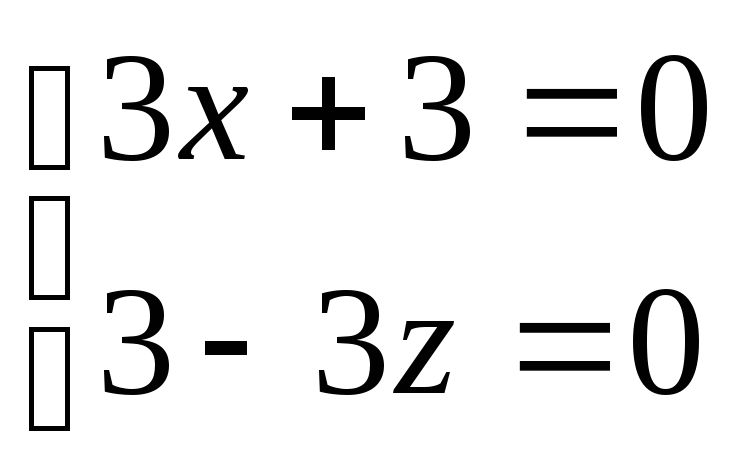
Решая эту систему находим
![]() .
.
![]()
Прямые
![]() будут пересекаться, если
будут пересекаться, если
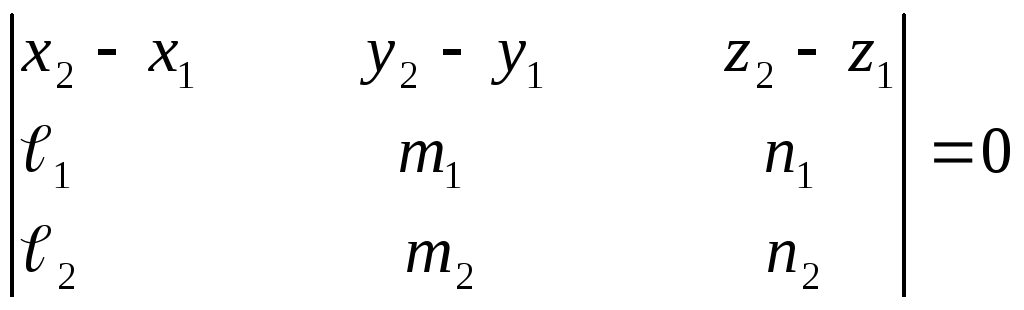
В нашем случае
![]()
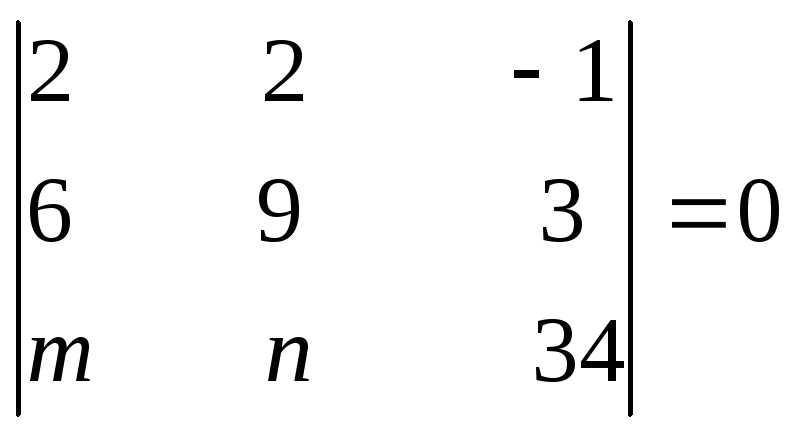
15m - 12n + 34 * 6 = 0.
(2)
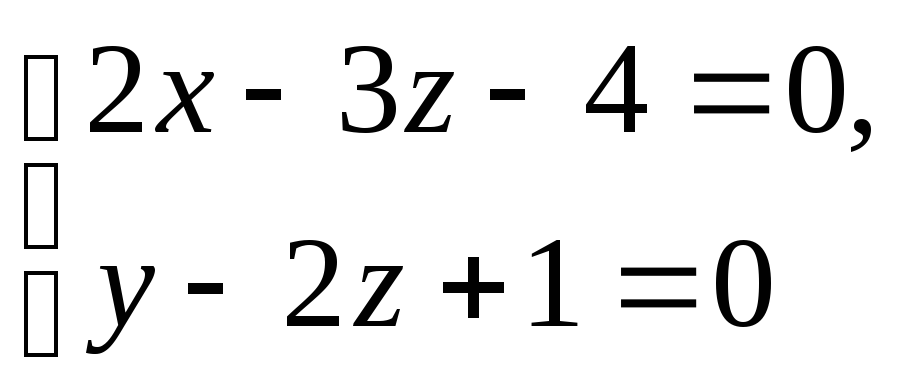
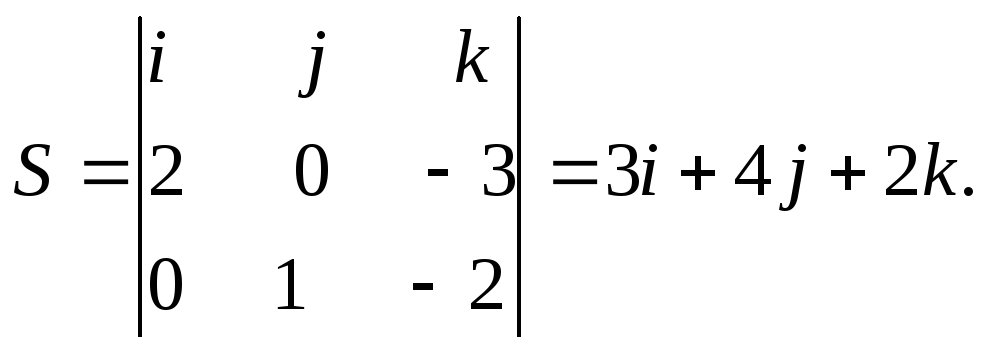
![]()
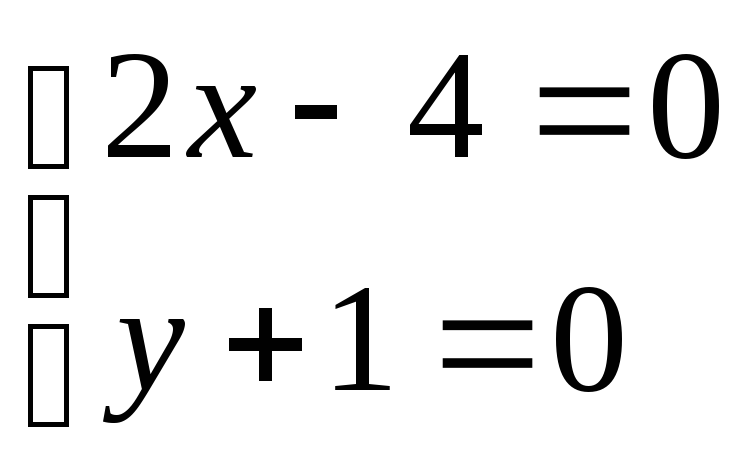
![]()
![]()
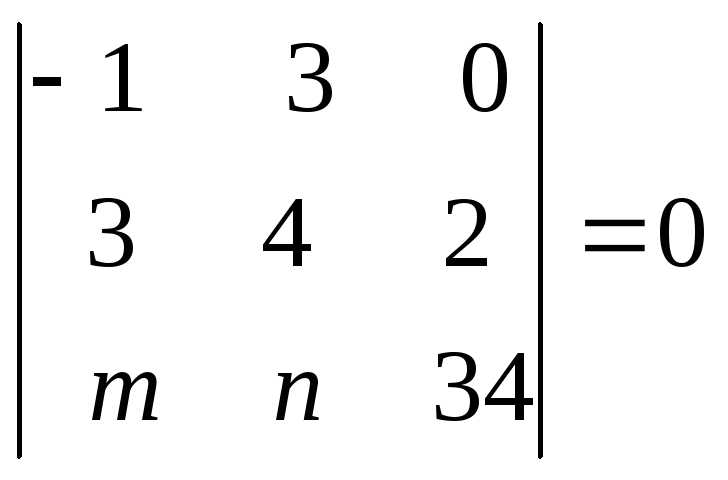
![]()
Теперь решим систему
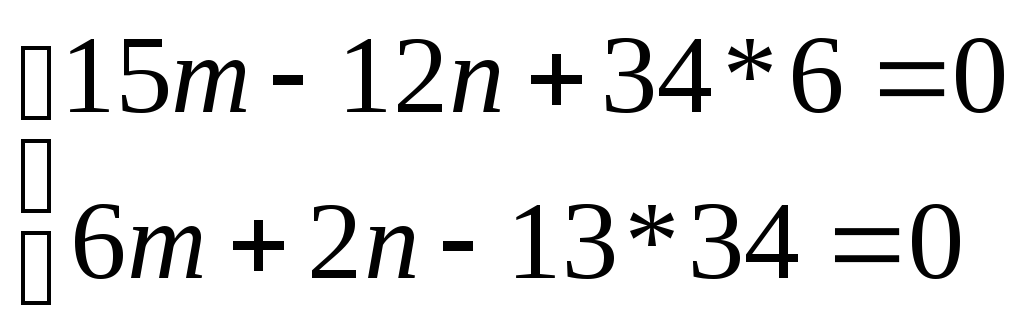
![]()
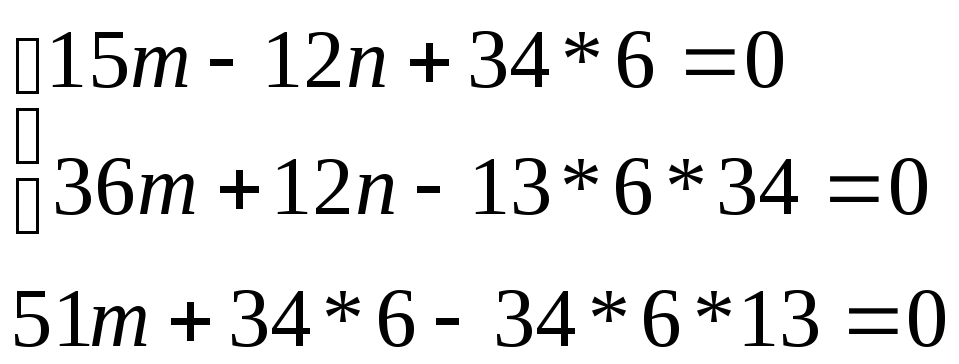
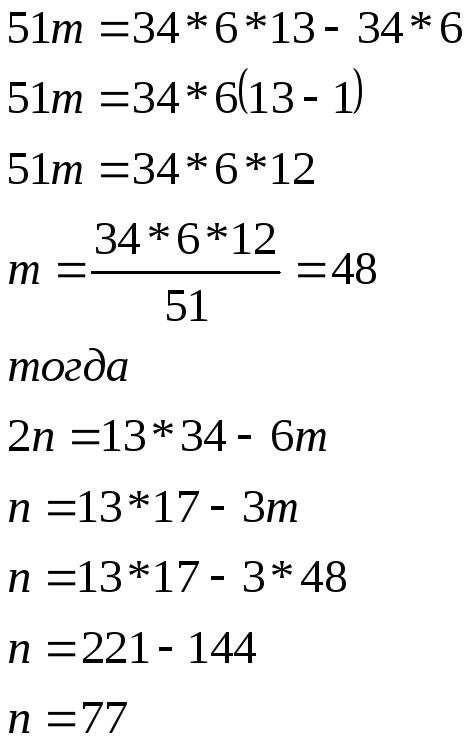
Ответ: m = 48; n = 77.
Задание 6.
Дано, что прямая, пересекающая ось
аппликат в точке
![]() параллельна плоскости
параллельна плоскости
![]() отстоит от неё на расстоянии 7 и
перпендикулярна оси координат. Найти
абсциссу точки пересечения этой
прямой с координатной плоскостью z
= 0.
отстоит от неё на расстоянии 7 и
перпендикулярна оси координат. Найти
абсциссу точки пересечения этой
прямой с координатной плоскостью z
= 0.
Решение.
Так как искомая прямая перпендикулярна
оси Oу, то она находится
в плоскости XOZ, и проходит
через точки
![]() .
.



 z
z ![]()



 y
y
 A
A

![]()
x
Так как она параллельна плоскости
![]() то расстояние между ними, равное 7,
это расстояние от какой либо точки
прямой до плоскости, которое вычисляется
по формуле:
то расстояние между ними, равное 7,
это расстояние от какой либо точки
прямой до плоскости, которое вычисляется
по формуле:
![]()
Имеем
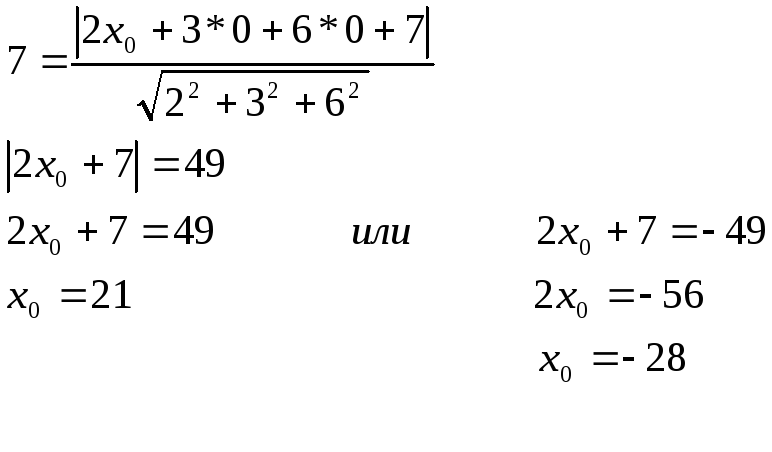
Ответ: абсцисса точки пересечения прямой с плоскостью z = 0 21 или -28.
Задание 7.
Записать уравнение касательной к
окружности
![]() в точке M(1, 2 ).
в точке M(1, 2 ).
Решение.
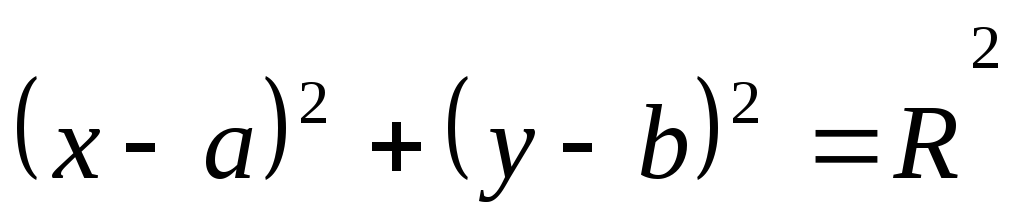
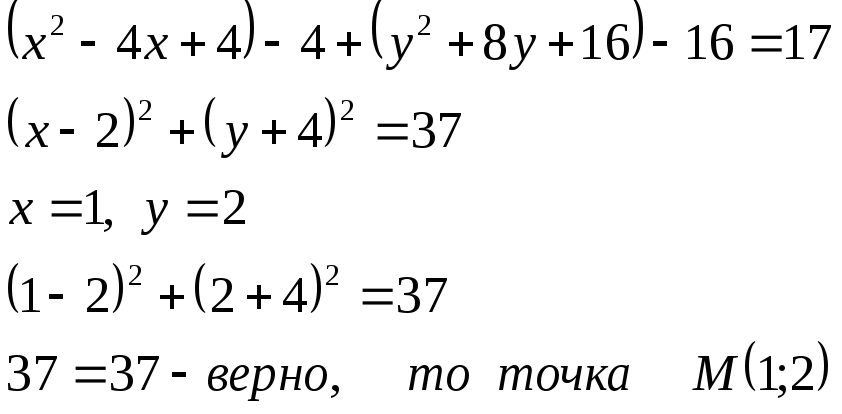
принадлежит окружности. Касательная
к окружности перпендикулярна радиусу,
проведенного в точку касания. В
качестве вектора нормали касательной
можно взять вектор
![]() где С ( 2; -4)- центр окружности.
где С ( 2; -4)- центр окружности.
СМ = ( -1; 6)
X –6y + c = 0
1 – 12 +c = 0
c = 11
x – 6y + 11 = 0 -искомое уравнение касательной.
Задание 8.
Дана кривая
![]()
8.1 Доказать, что эта кривая - эллипс.
-
Найти координаты центра его симметрии.
-
Найти его большую и малую полуоси.
-
Записать уравнение фокальной оси.
-
Построить данную кривую.
Решение.
8.1
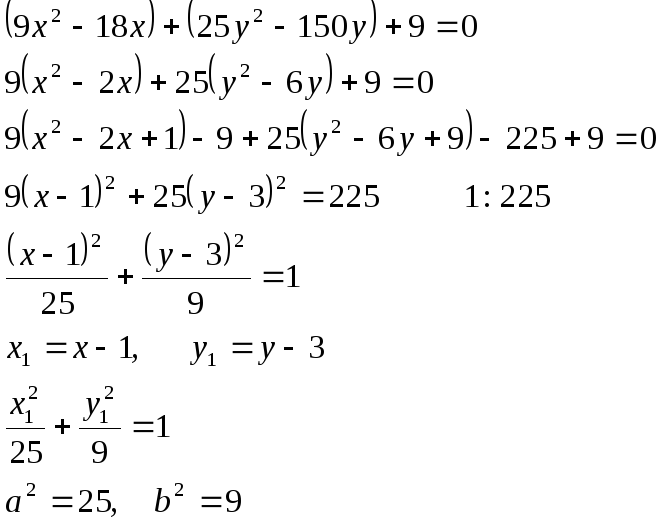
8.2 Центр его симметрии находится в точке ( 1; 3 ).
8.3 Большая полуось а = 5
Малая полуось в = 3
8.4 Уравнение фокальной оси у = 3.
8

 .5.
.5. ![]()


 у
у ![]()






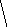
![]()
![]()


![]()

![]()





![]()
![]()
![]()
![]()
111





0 1 X
Задание 9.
Дана кривая
![]()
9.1. Доказать, что данная кривая - парабола.
-
Найти координаты её вершины.
-
Найти значение её параметра p.
-
Записать уравнение её оси симметрии.
-
Построить данную параболу.
Решение.
9.1.
![]()
-
это Уравнение параболы, симметричной относительно оси
 .
.
9.2. Вершина параболы ( 5; 0)
9.3 Сравнивая уравнение параболы с
каноническим уравнением параболы
![]() находим
находим
2p = -2, откуда p = - 1.
9.4.Ось симметрии х = 5.
9.5.
 y
y
5





 1 x
1 x


Задание 10.
10.Дана кривая
![]()
10.1.Доказать, что эта кривая - гипербола.
10.2.Найти координаты её центра симметрии.
10.3.Найти действительную и мнимую полуоси.
10.4.Записать общее уравнение фокальной оси.
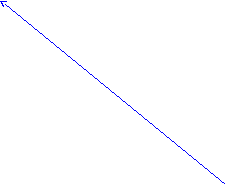
10.5.Построить данную гиперболу.
Решение.
10.1.
![]()
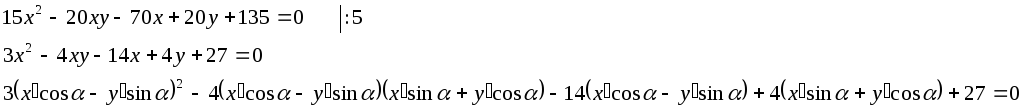
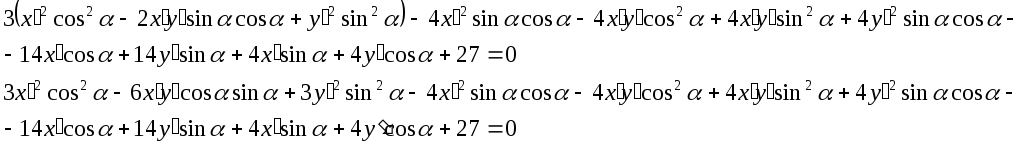
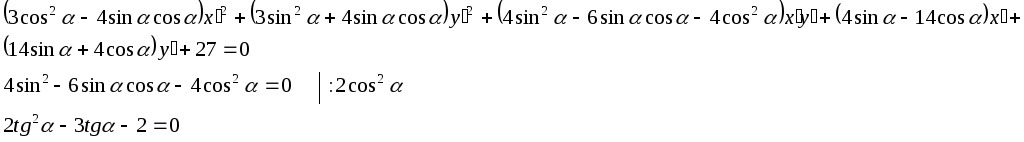
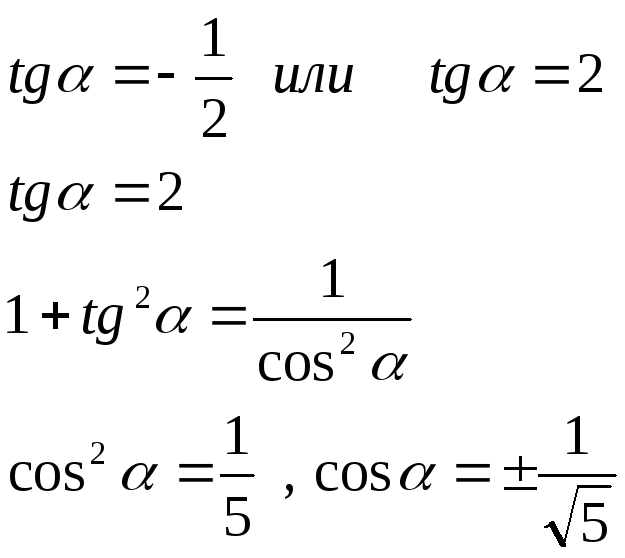

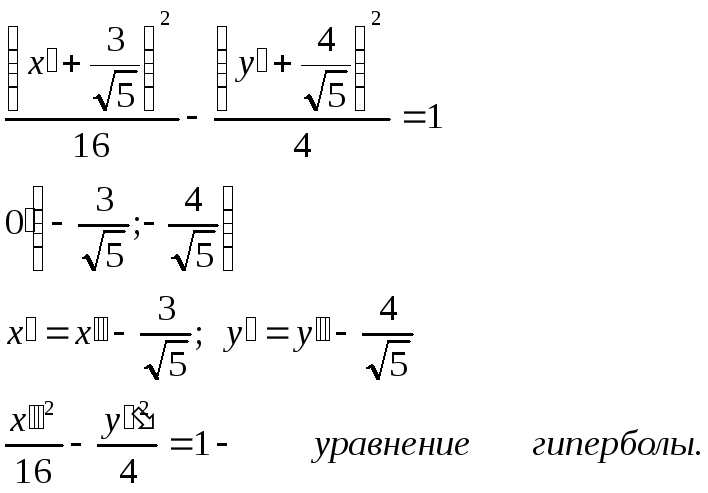
10.2. Координаты её центра симметрии
![]()
10.3.Число 4 – действительная полуось.
Число 2 – мнимая полуось.
1

 0.4. y
0.4. y


![]()
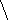
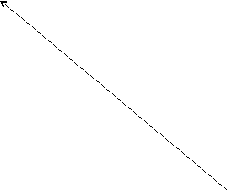
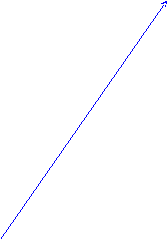
![]()
![]()

![]()


![]()




 A1
A1


 B1 0
B1 0
1 x
![]()

B2


 A2
A2
 F2
F2