
Контрольная работа 2 / 2- 1_Высшая математика_7
.doc
Контрольная работа №2 по высшей математике
выбор варианта по формуле
![]()
1
Дано: М1 (-1,2) М2 (-3,-2)
Найти: 1. Уравнение прямой М1М2
2. Параметры k и b
Решение:
X
=
-3+1 -2 - 2
X
=
-2 -4
X
=
1 2
2X+2 = Y-2
2X – Y + 4=0 – общее уравнение прямой М1М2
![]()
![]()
Ответ: уравнение прямой 2X –Y + 4 = 0 ; k = 2 , b = 4
2
Дано: 5x – 12y – 65 = 0 5x – 12y + 65 = 0
Найти: Площадь квадрата, две стороны которого расположены на данных прямых.
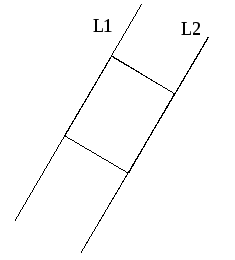
Решение:
Прямые L1: 5x – 12y – 65 = 0 и L2: 5x – 12y + 65 = 0 параллельны
Значит сторона квадрата должна равняться расстоянию
между || прямыми L1 и L2
Возьмём точку М(1,-5) принадлежащую прямой L1
![]()
S квадрата =![]()
Ответ: S квадрата=49
3
Дано: плоскости 4x + y – 3z + 13=0 и x – 2y + z – 11=0
P ( -3 , 2 , 5 )
Найти : уравнение плоскости, проходящей через перпендикуляры, опущенные из точки P на данные плоскости.
Решение:
![]()
![]()
составим уравнение плоскости, проходящей через точки Р(-3,2,5) и параллельно векторам N1(4,1,-3) , N2(1,-2,1)
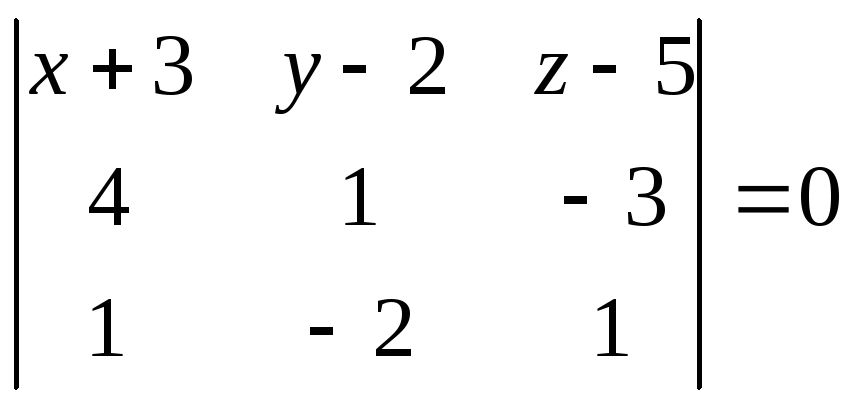
![]()
![]()
-5x – 15 - 7y + 14 - 9z + 45 = 0
5x + 7y + 9z – 44 = 0
Ответ: 5x + 7y + 9z – 44 = 0
4
Дано :
![]() 2x + y – z
– 6 = 0 и 2x + y
– z – 4 = 0
2x + y – z
– 6 = 0 и 2x + y
– z – 4 = 0
Найти : длину отрезка прямой | |
![]() ,
между точками пересечения этой прямой
с плоскостями.
,
между точками пересечения этой прямой
с плоскостями.
Решение: Плоскости 2x + y – z – 6 = 0 и 2x + y – z – 4 = 0 параллельны
Подберём координаты точки А
![]()
![]() А(0,3,-1)
А(0,3,-1)
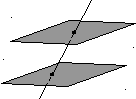 Составим уравнение прямой , проходящей
через
Составим уравнение прямой , проходящей
через
В
через точку А с направляющим вектором
![]()
![]()
![]()
![]()
![]() 4y
– 12 – 3z – 3 = 0
4y
– 12 – 3z – 3 = 0
![]() 4y
– 3z – 15 = 0 – уравнение
прямой АВ
4y
– 3z – 15 = 0 – уравнение
прямой АВ
А Найдём координаты точки В:

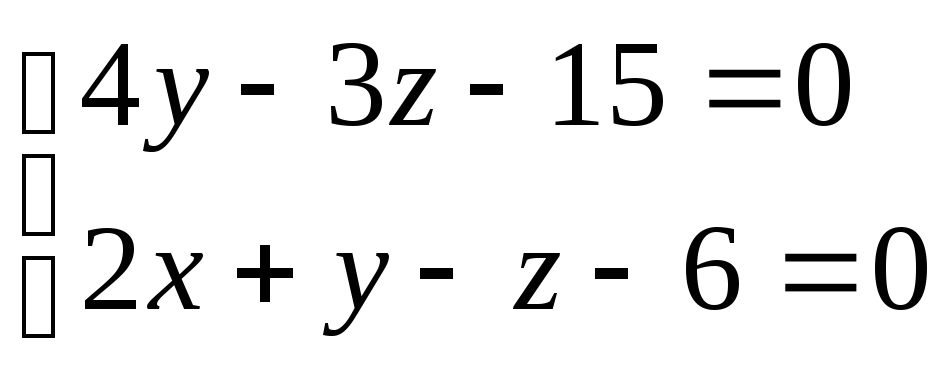 т.к. x=0
т.к. x=0
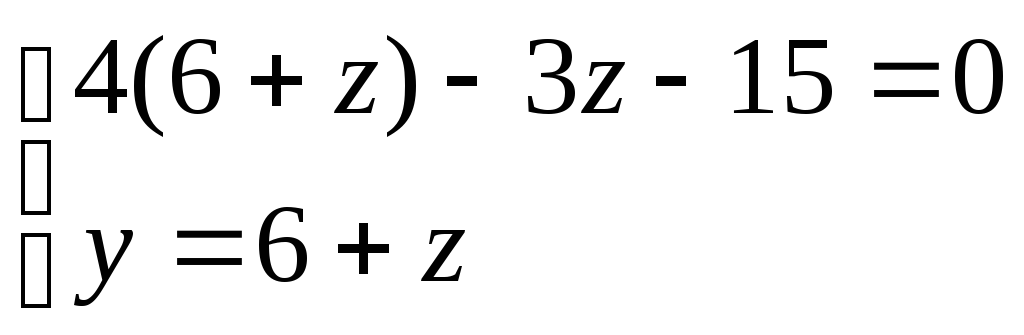
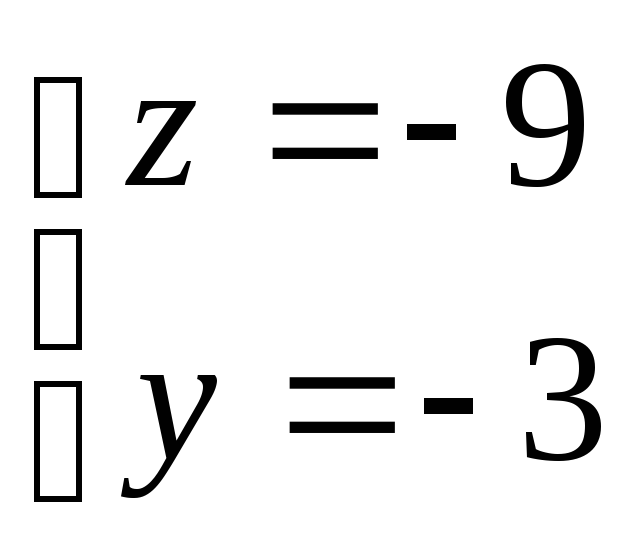
В ( 0, -3 , -9 )
![]() ( 0, - 6, -8 )
( 0, - 6, -8 )
![]()
Ответ: длинна отрезка равна 10
5
1)
![]() и
и
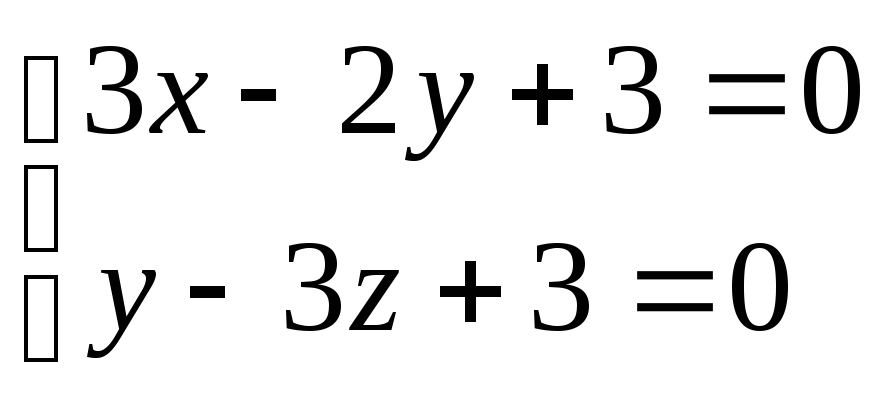
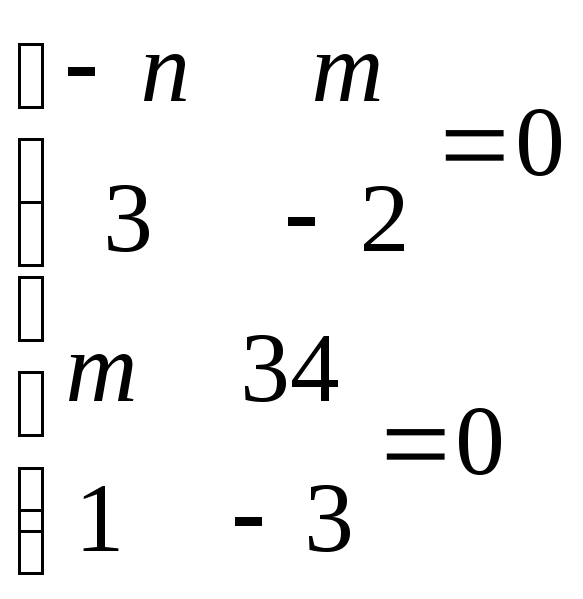
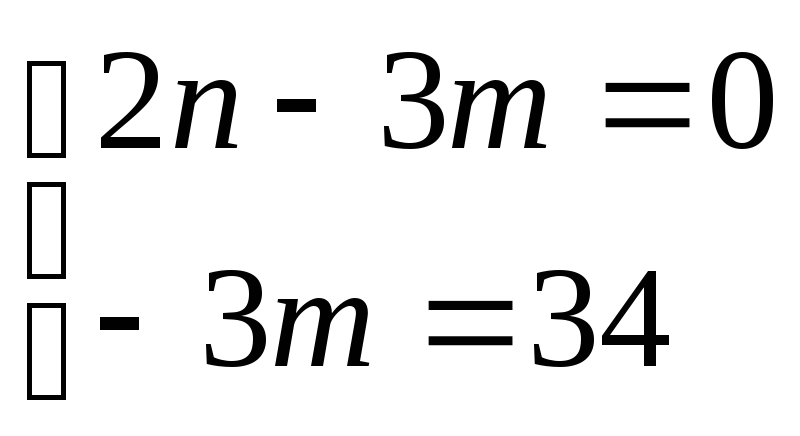
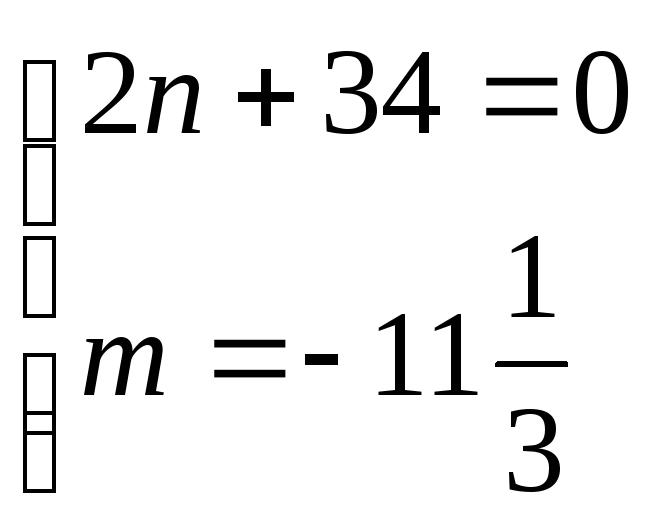
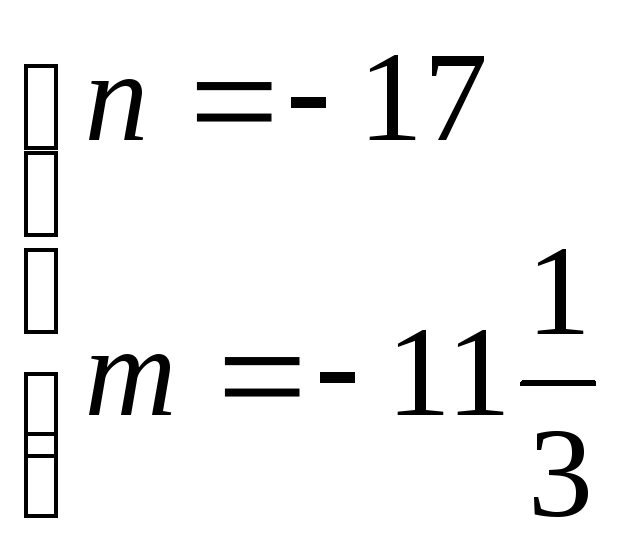
2)
![]() и
и
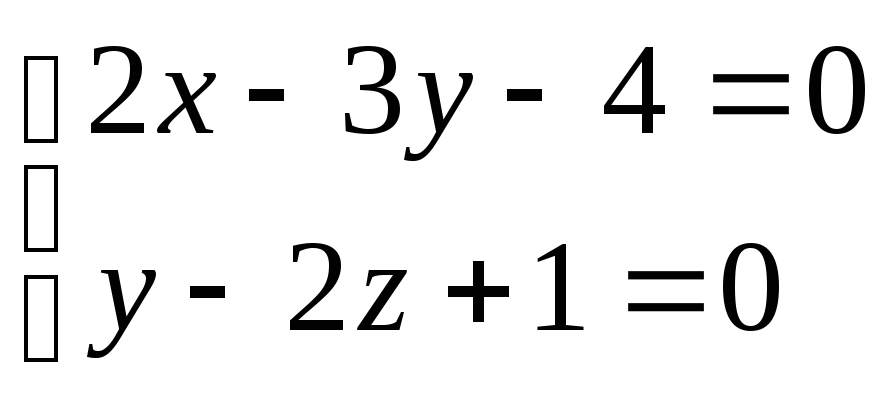
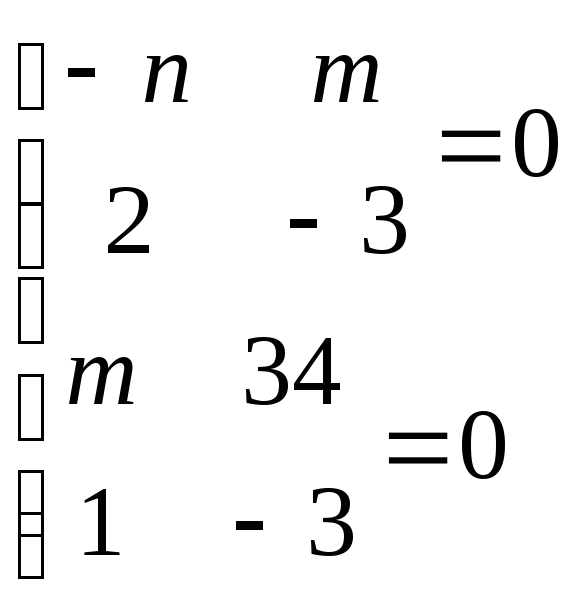
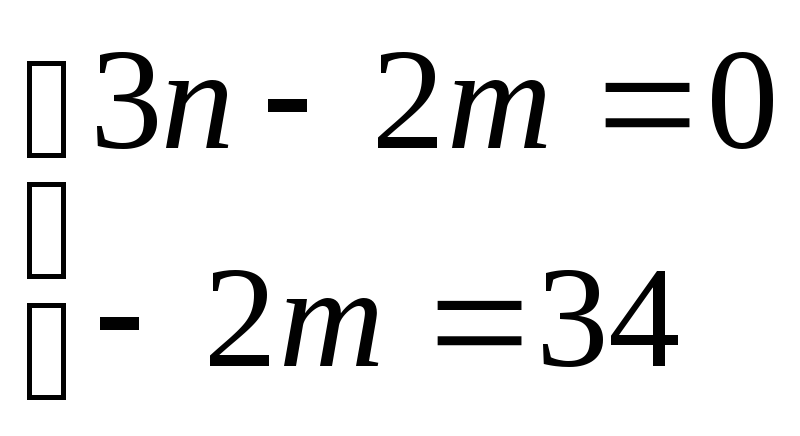
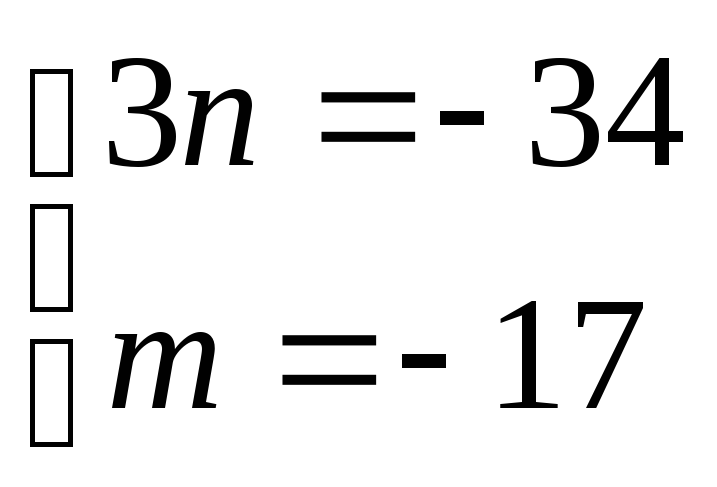
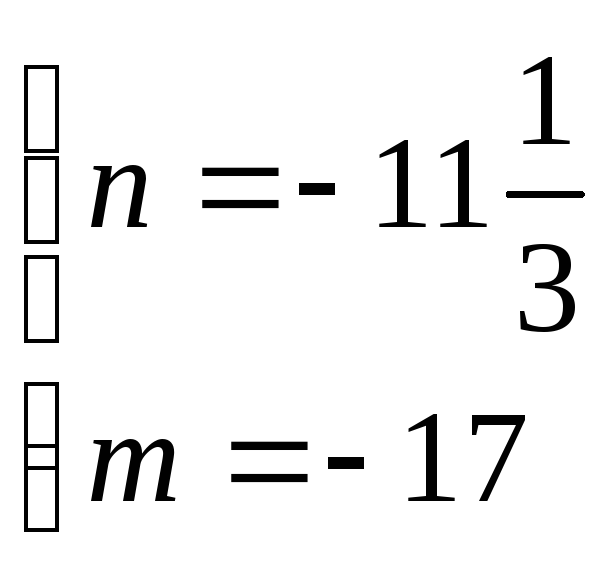
Ответ: пересекается с прямой
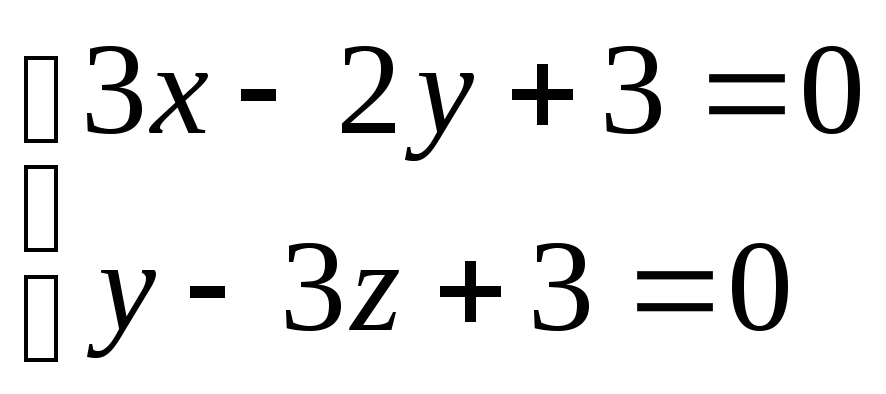 при n=
- 17 m= -11
при n=
- 17 m= -11![]()
пересекается с прямой
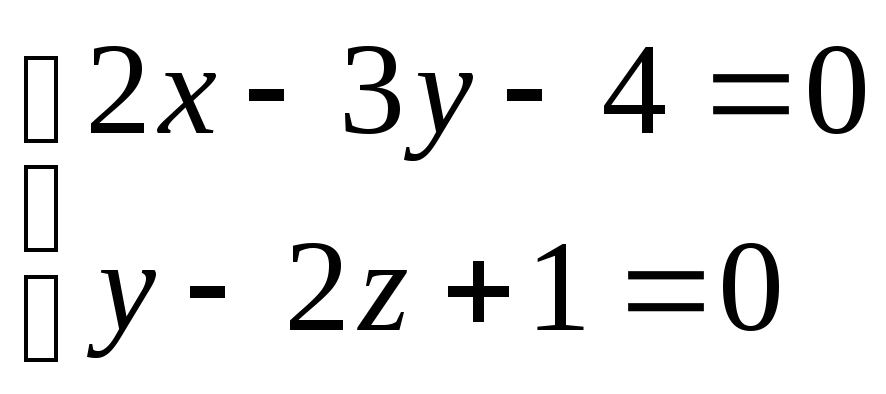 при n=
-11
при n=
-11![]() m= - 17
m= - 17
6
Дано: М
(0,0,Z![]() )
, Z
)
, Z![]() >0
d = 7
>0
d = 7
2x + 3y +6z + 7 = 0
d =![]()
![]()
![]()
![]()
![]()
Ответ: M (0,0,7) – точка пересечения прямой с осью аппликат.
7
Дано: Окружность
![]() точка М ( 1 , 2 )
точка М ( 1 , 2 )
Найти: уравнение касательной к данной окружности в точке М
Решение:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
-2(x - 1) + 12(y - 2)=0
-2x +2 + 12y - 24=0
2x - 12y +22=0
x - 6y + 11=0
Ответ: x - 6y + 11=0
8
![]()
-
Докажем, что данная кривая – эллипс.
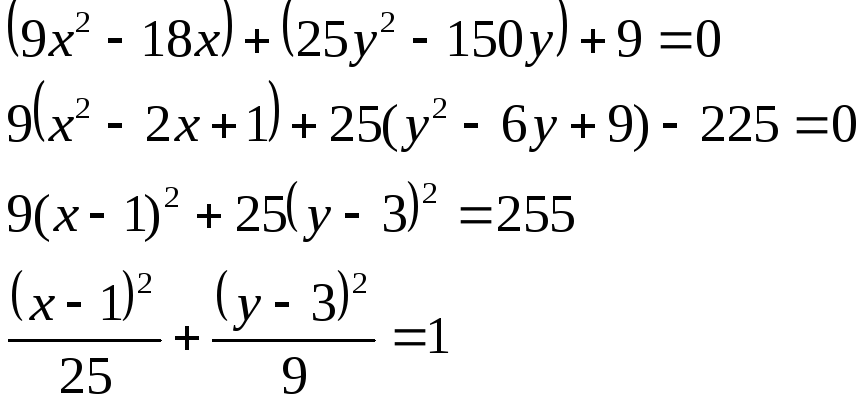
![]() - Уравнение эллипса
- Уравнение эллипса
-
Найдём координату центра симметрии эллипса
![]() x=1 y=3
x=1 y=3
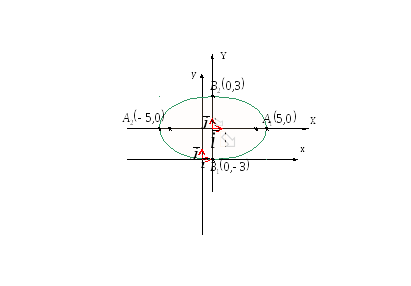
( 1,3 ) - координата центра симметрии
-
a=5 – большая полуось
b=3 – малая полуось
-
Запишем уравнение фокальной оси: Приведём квадратичную форму
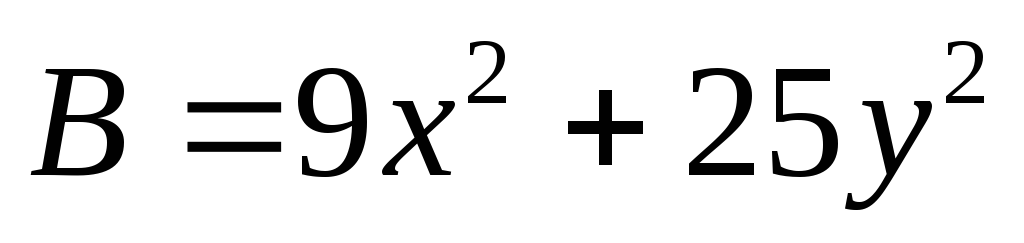 к главным осям.
к главным осям.
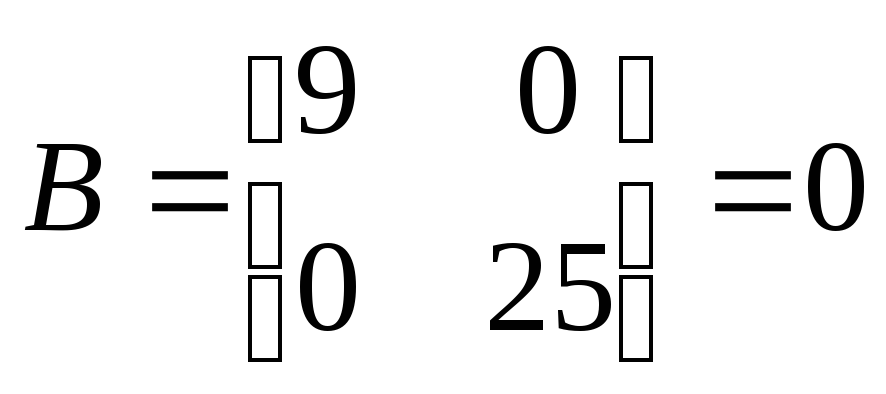 Характеристическое
уравнение этой матрицы:
Характеристическое
уравнение этой матрицы:

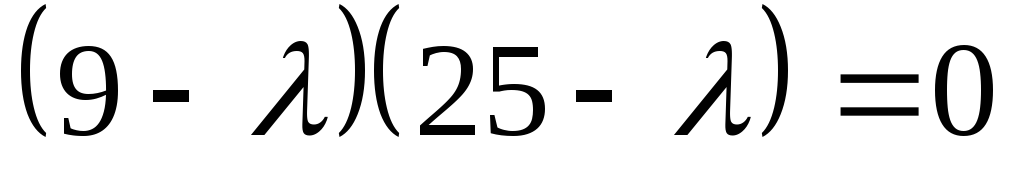
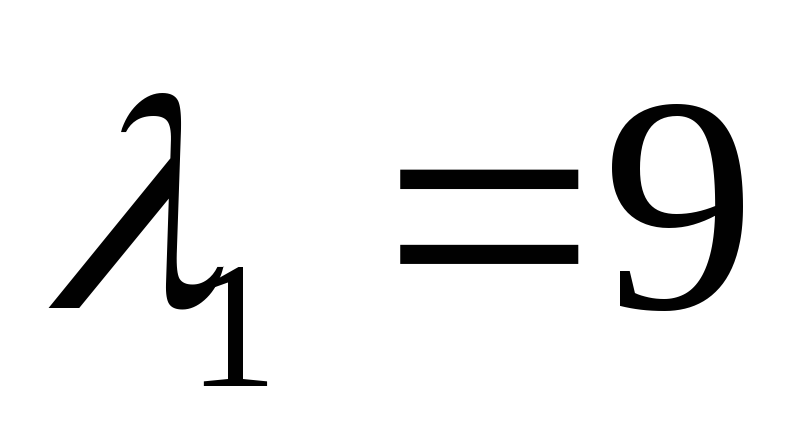
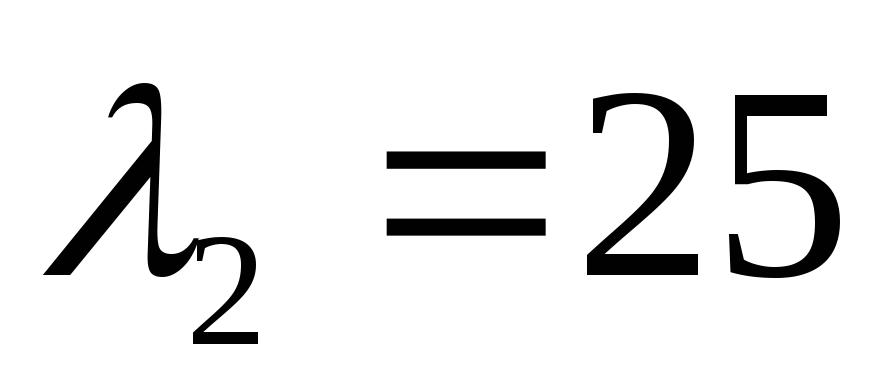
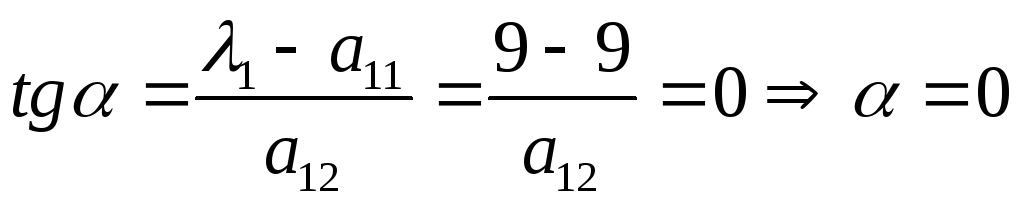
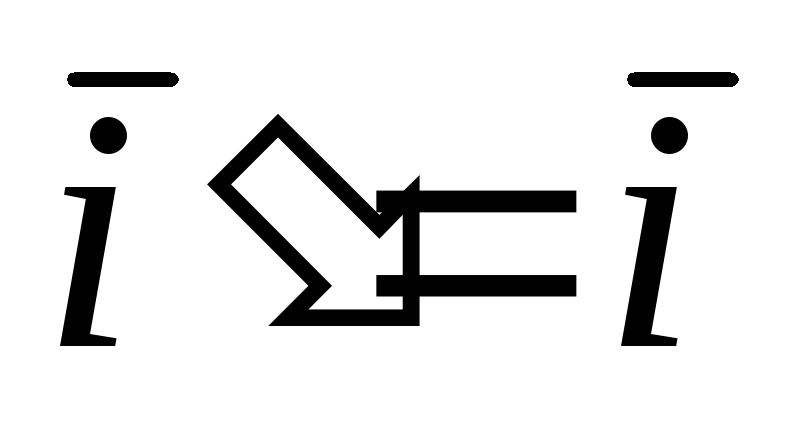
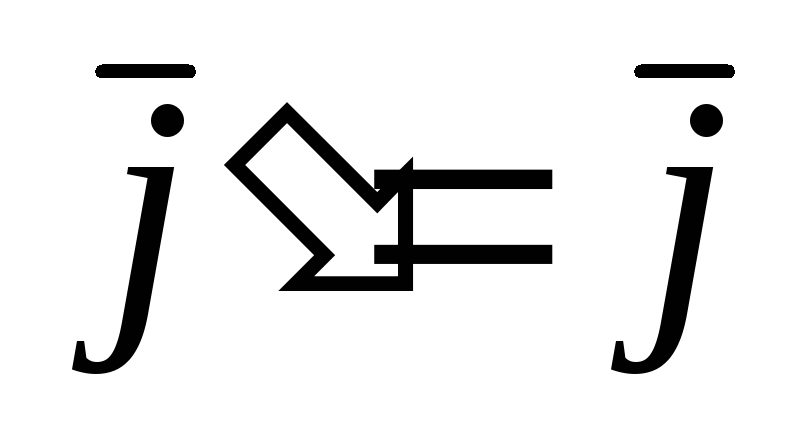
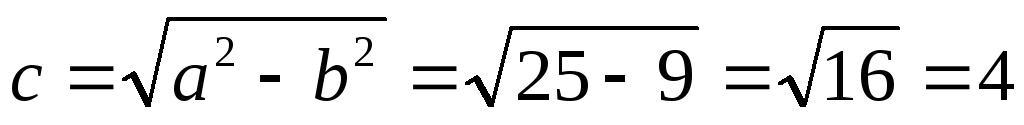
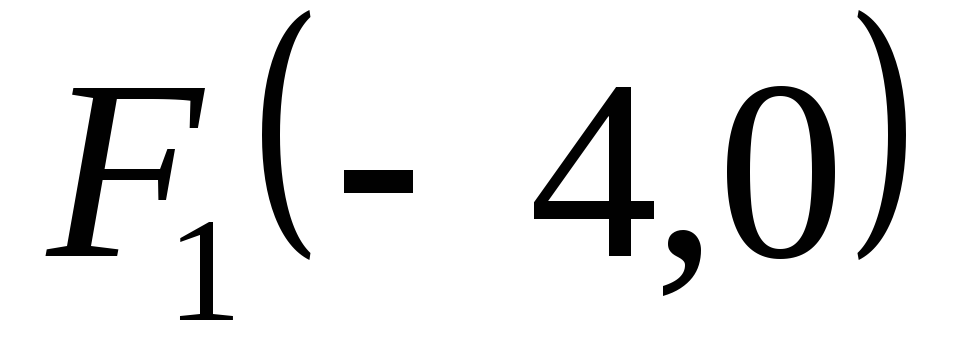
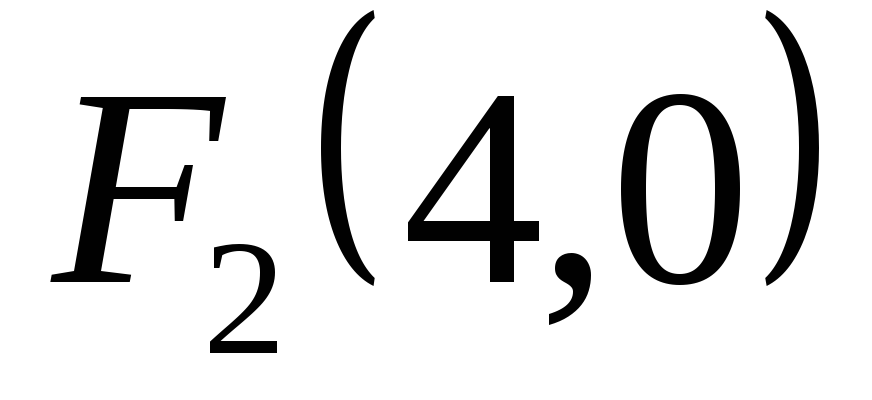 — фокусы
y=0 – фокальная
ось
— фокусы
y=0 – фокальная
ось -
Построим данную кривую:

9
Дана кривая
![]()
-
Докажем, что данная кривая – парабола.
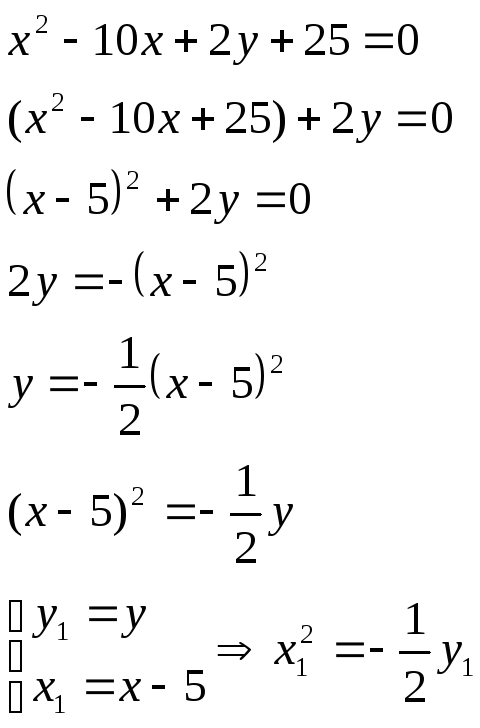
9.2. Координата вершины – ( 5 , 0 )
9.3. Найдём значение параметра – Р
2р = –![]()
р =![]()
9.4. Запишем уравнение оси симметрии
Приведём квадратичную форму
![]() к главным осям
к главным осям
Её матрица
![]()
Запишем характеристическое уравнение
![]()
![]()
![]() и
и
![]()
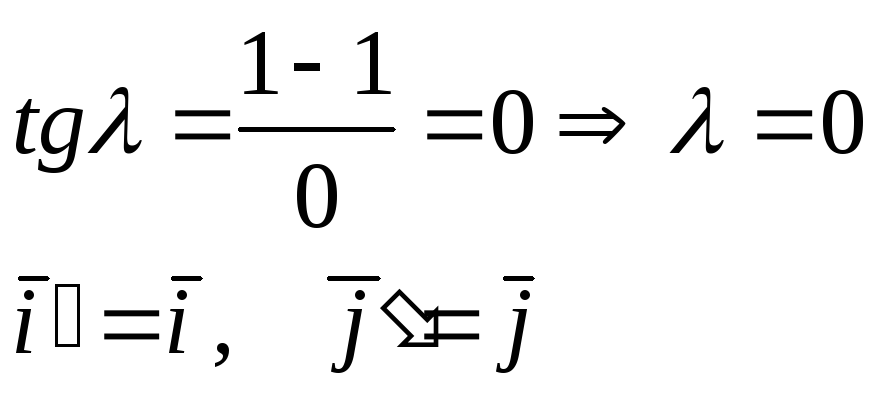
x = 5 – ось симметрии
9.5.

10
Дано: кривая
![]()
10.1. Докажем, что эта кривая – гипербола.
Приведем квадратичную форму
![]() к главным осям.
к главным осям.
Её матрица
![]() .
.
Записываем характеристическое уравнение этой матрицы.
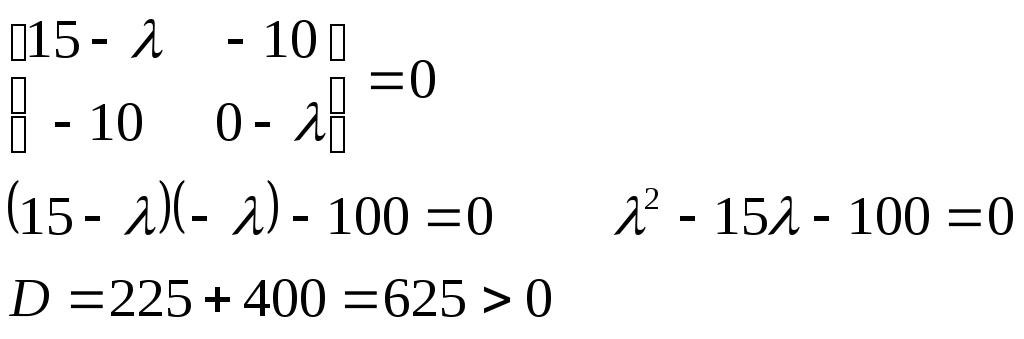
![]()
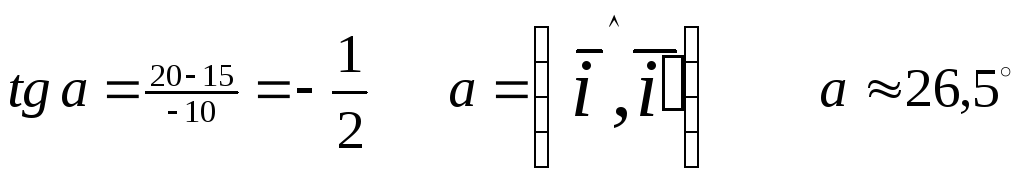
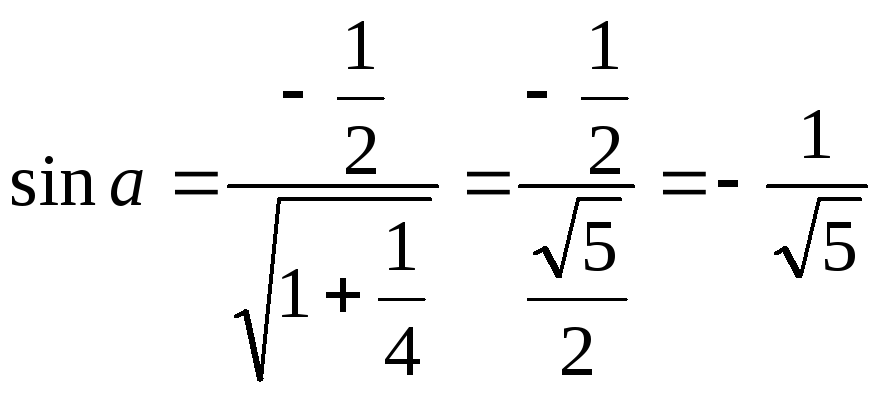
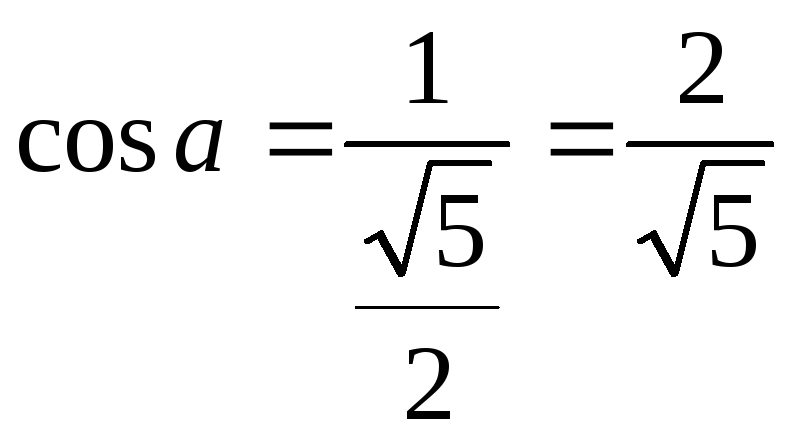
![]()
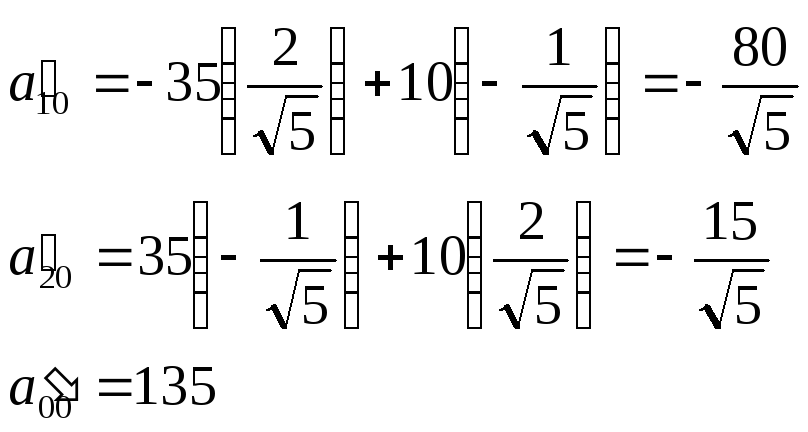

10.2.
![]() – Координата центра
– Координата центра
-
Действительная полуось b=4
Мнимая полуось a=2
-
Запишем уравнение фокальной оси
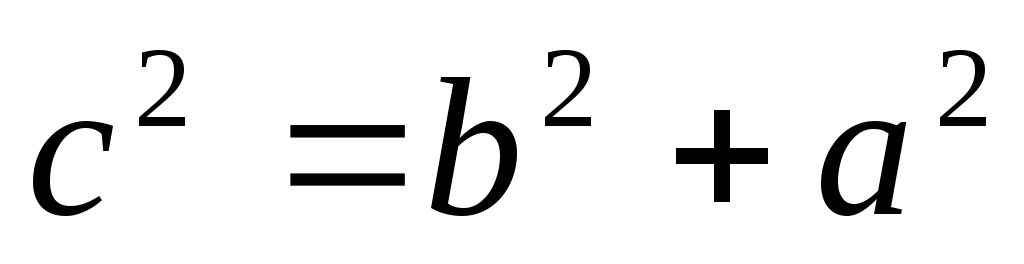
![]()
![]()
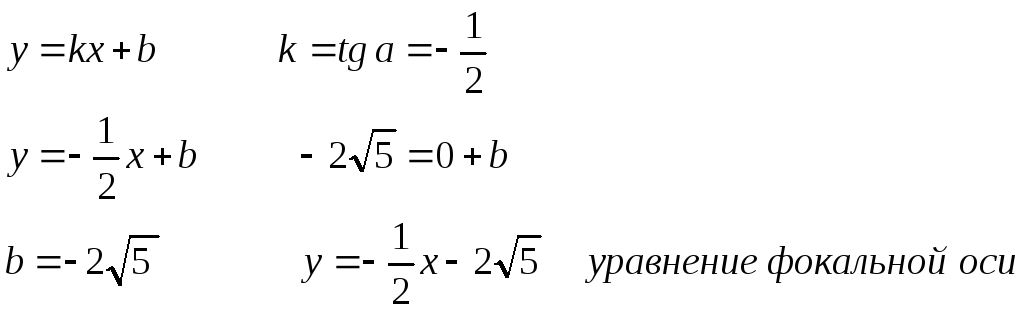
![]()
![]() –
Общее уравнение фокальной оси.
–
Общее уравнение фокальной оси.
-
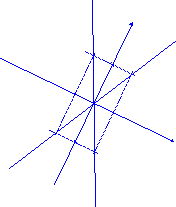
Построим данную гиперболу
y
![]()

![]()

 Y
Y


![]()
![]()
0
![]()

![]()

-a
![]() 0
0![]()
![]()
- b
b

![]() X
X
