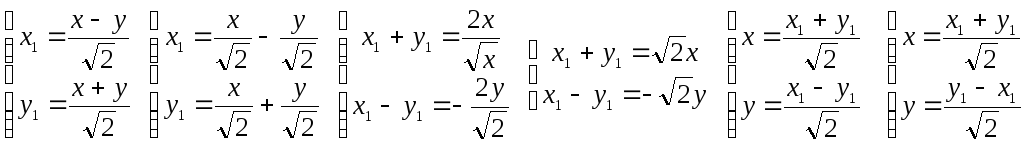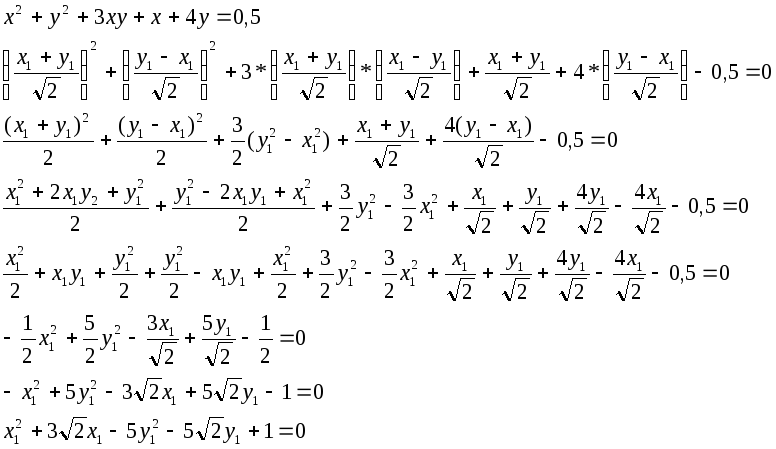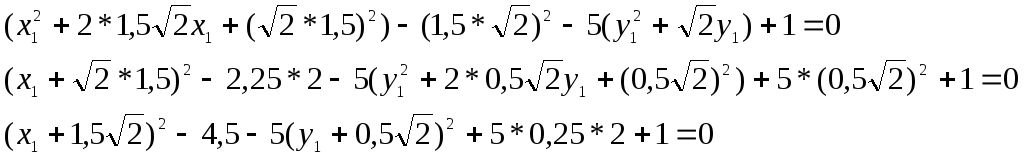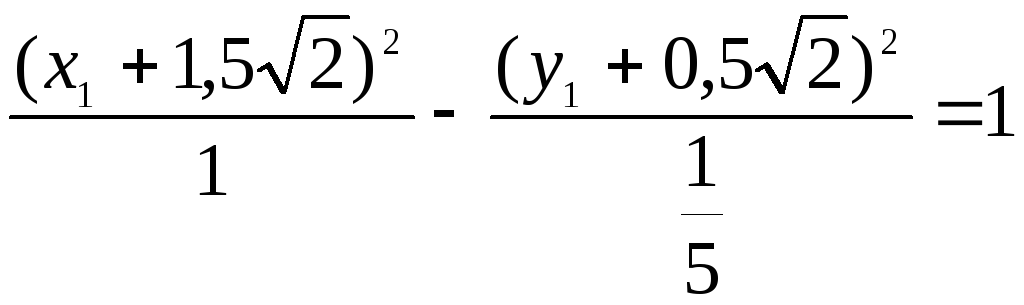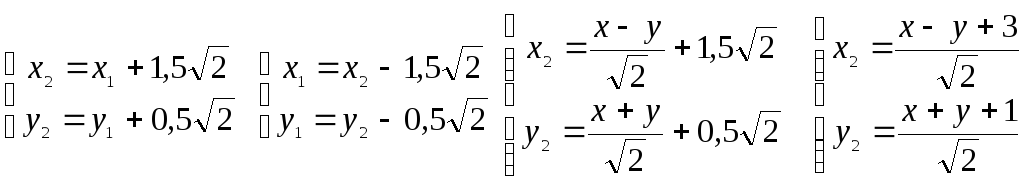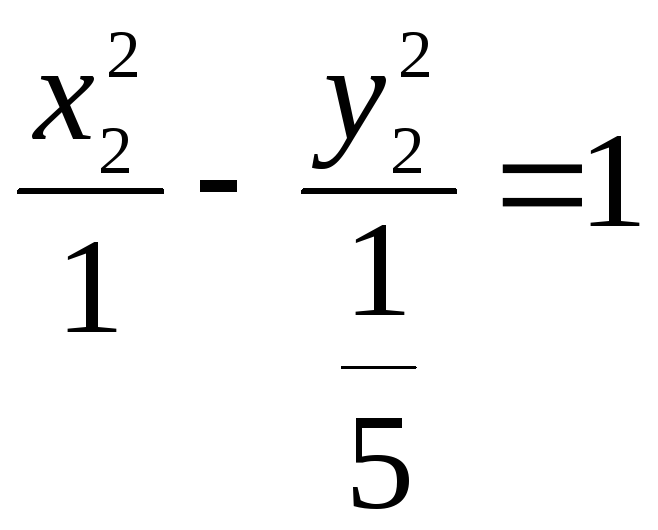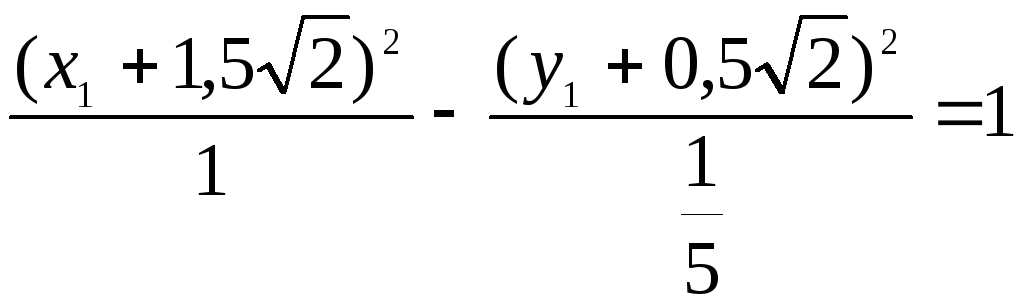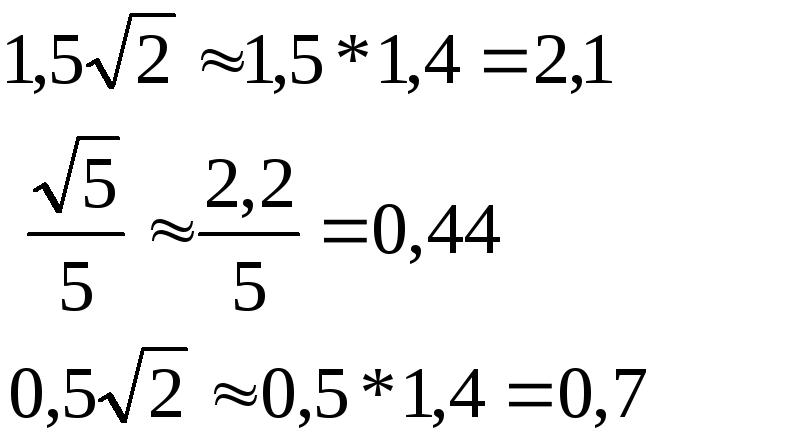Контрольная работа 2 / 2- 2.7_Высшая математика-1
.doc
|
Федеральное агентство РФ по образованию. Томский университет систем управления и радиоэлектроники.
Контрольная работа
по дисциплине: “Высшая математика Линейная алгебра и аналитическая геометрия” Автор: Л.И. Магазинников А.Л. Магазинников Контрольная работа №2. Вариант №.2.7.
Выполнил: Студент ТМЦДО
2007 г. |
|
При решении контрольной работы используется учебное пособие Магазинников Л.И., Магазинников А.Л. Высшая математика. Линейная алгебра и аналитическая геометрия: Учебное пособие. - Томск: Томский межвузовский центр дистанционного образования, 2003.-176с. 1. Запишите общее уравнение прямой, проходящей через точку М(2,4) перпендикулярно прямой 3х+4у+5=0. РЕШЕНИЕ: В
качестве вектора нормали прямой L
можно принять вектор, перпендикулярный
вектору
Если
пряма проходит через точку
получаем:
Ответ: 4x-3y+4=0 2. Составьте уравнения прямых, проходящих через точку Р(3,5) на одинаковых расстояниях от точек А(-7,3) и В(11,-15). В ответ ввести уравнение той прямой, которая отсекает от осей координат треугольник, расположенный в первой четверти. РЕШЕНИЕ: Будем искать уравнение в виде Ax+By+C=0 так как эта прямая проходит через точку Р, то 3А+5В+С=0 Прямая Ах+Ву+с=0 находится на одинаковом расстоянии от точек А(-7,3) и В(11,-15). Используя
формулу
получаем
Для отыскания неизвестных коэффициентов А, В, С получаем две различные системы уравнений 1)
Решаем первую систему уравнений 1)
Подставим в уравнение Ax+By+C=0 найденные значения, получим
Решаем вторую систему уравнений 2)
Подставим в уравнение Ax+By+C=0 найденные значения, получим
Общее решение искомой прямой можно записать в виде х+у-8=0 или 11х-у-28=0 Уравнение прямой, которая отсекает от осей координат треугольник, расположенный в первой четверти х+у-8=0 у=-х+8 Ответ: х+у-8=0
РЕШЕНИЕ: Уравнение плоскости проходящей через данные точки параллельно вектору АВ имеет вид:
Ответ: х+2у-z-7=0
РЕШЕНИЕ: Запишем уравнение прямой в параметрическом виде:
Направляющий вектор J=(4,3,-2) можно принять в качестве вектора нормали плоскости N. Записываем уравнение плоскости N: 4х+3у-2z+D=0 Так как точка начала координат О(0,0,0) лежит в плоскости P, то 4*0+3*0-2*0+D=0 D=0 Уравнение плоскости N имеет вид: 4х+3у-2z=0 Найдем точку пересечения прямой с плоскостью N. Находим
то значение параметра
Так
как точка
Полагая
в параметрическом уравнении прямой
Ответ: (1, -2, -1)
РЕШЕНИЕ: условие параллельности прямой с направляющими координатами e, m, n и плоскости Ax+By+Cz+D=0 есть Ae+Bm+Cn=0 Найдём направляющий вектор прямой
то
есть
Плоскость: x+3y+Cz-2=0 где А=1, В=3, С=С 1*1+3*1+С*2=0 1+3+2С=0 2С=-4 С=-2 Ответ: С=-2 6. Две грани куба лежат на плоскостях 3x-6y+2z-5=0 и 3x-6y+2z+30=0. Вычислите объём куба. РЕШЕНИЕ: Данные плоскости параллельны так как выполняется условие
На плоскости 3x-6y+2z-5=0 возьмём произвольную точку Р с координатами х=2, у=1 тогда 2z=-3x+6y+5 z=(-3x+6y+5)/2 z=(-3*2+6*1+5)/2 z=5/2=2,5 точка Р (2; 1; 2,5), на плоскости 3x-6y+2z+30=0 найдём точку Q, являющуюся проекцией точки Р. Запишем параметрическое уравнение прямой проходящеё через точку Р
3*(3t+2)-6*(-6t+1)+2*(2t+2,5)+30=0 9t+6+36t-6+4t+5+30=0 49t+35=0 49t=-35 t=-35/49 t=-5/7 Найдём координаты точки Q:
Длинна ребра куба, равна длине отрезка PQ:
Ответ: 173,74
найдите
координаты
РЕШЕНИЕ: Выделяем полные квадраты:
Заданная кривая- сфера с центром в точке М(2, -3, 4) и радиусом R=8 Ответ: (2, -3, 4, 8)
8.
Дана кривая
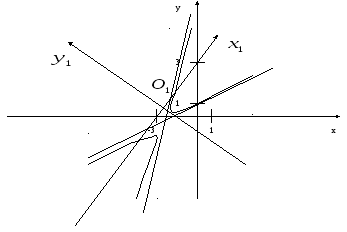
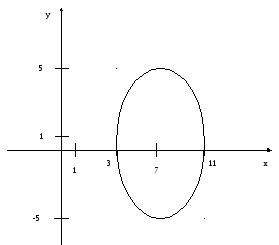
8.1. Докажите, что эта кривая – эллипс. 8.2. Найдите координаты центра его симметрии. 8.3. Найдите его большую и малую полуоси. 8.4. Запишите уравнение фокальной оси. 8.5. Постройте данную кривую. РЕШЕНИЕ:
Данная кривая- эллипс. Координаты центра его симметрии (7; 0) Большая полуось: а=4 Малая полуось: в=5 Уравнение фокальной оси: у=0
9. Дана
кривая
9.1 Докажите что данная кривая кривая- парабола. 9.2 Найдите координаты её вершины. 9.3 Найдите значение её параметра р. 9.4 Запишите уравнение её оси симметрии. 9.5 Постройте данную параболу. РЕШЕНИЕ:
Данная кривая- парабола. Координаты её вершины (8; 0). Находим значение её параметра р:
то есть 2р=14, р=7. Уравнение её оси симметрии х=8
10. Дана
кривая
10.1 Докажите что данная кривая- гипербола. 10.2 Найдите координаты её центра симметрии. 10.3 Найдите квадраты её действительной и мнимой полуосей. 10.4 Запишите общее уравнение фокальной оси. 10.5 Постройте данную гиперболу. РЕШЕНИЕ: Квадратичную
форму В(х,у)=
Так как собственные числа имеют разные знаки, то данное уравнение определяет кривую гиперболического типа. Находим
собственные векторы матрицы В. Для
собственного числа,
Положим
Другой
базисный вектор
Записываем
матрицу Q
перехода от базиса
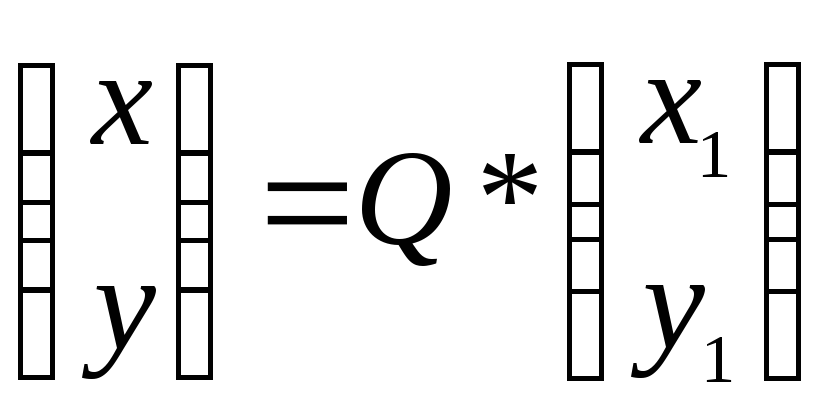
Старые
координаты (х;у)
связанны с новыми
В новой системе координат уравнение данной кривой примет вид:
Выделяя полные квадраты, получаем:
Действительная полуось а=1 Мнимая
полуось в= Произведём
преобразование параллельного переноса
системы координат в новое начало
В
системе координат
Оси
Фокальной осью является прямая : у=0. Для построения гиперболы строим в старой системе координат новую систему, в которой строим данную гиперболу:
где:
|
|
|


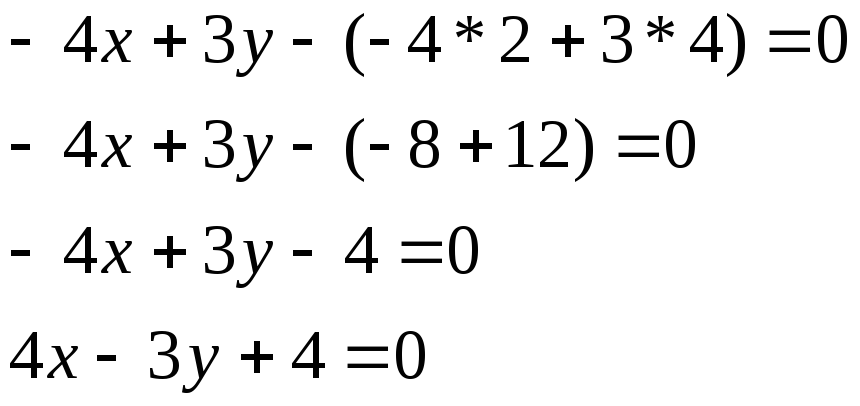
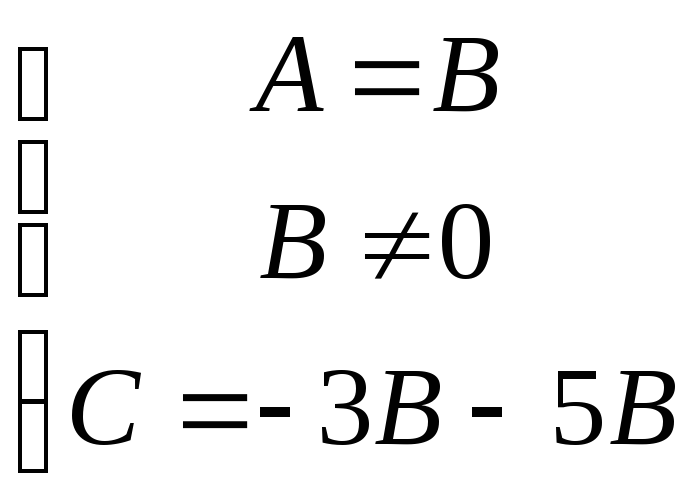
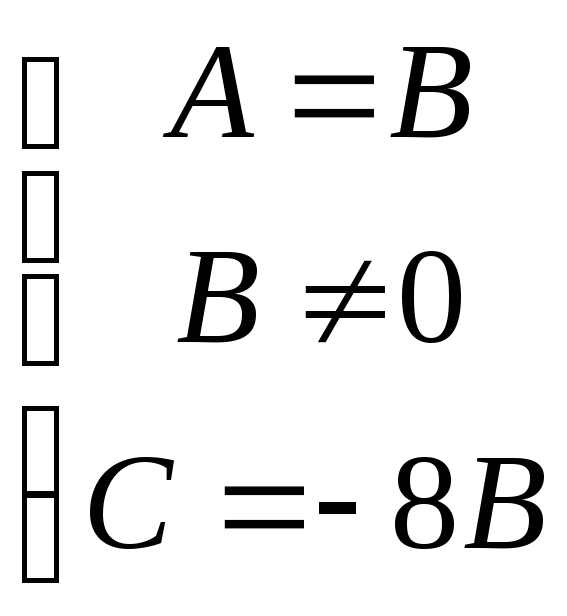
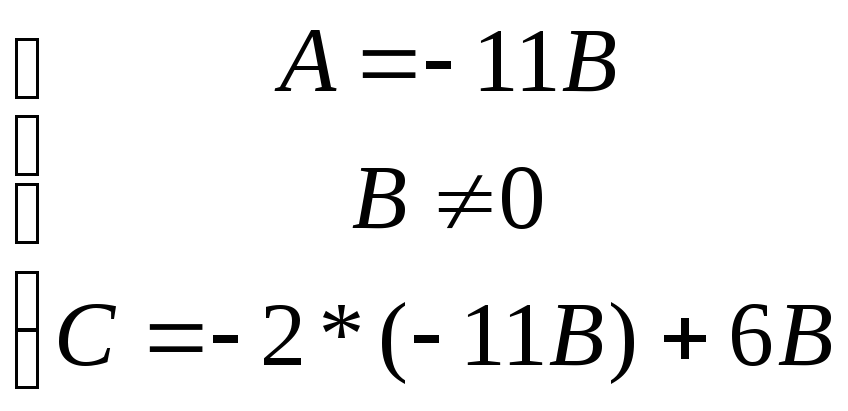
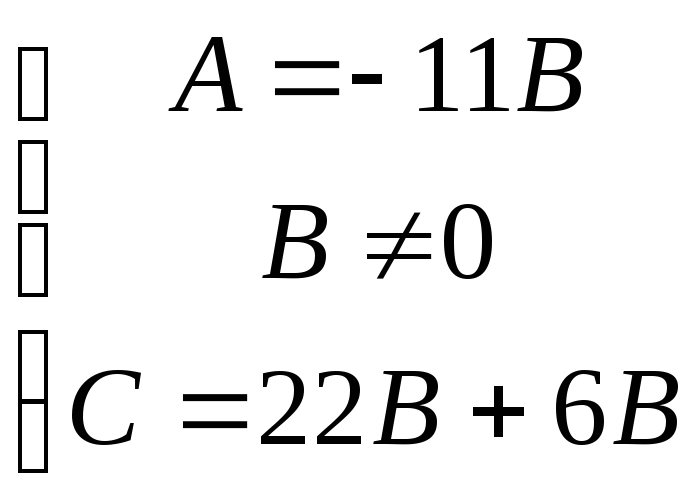
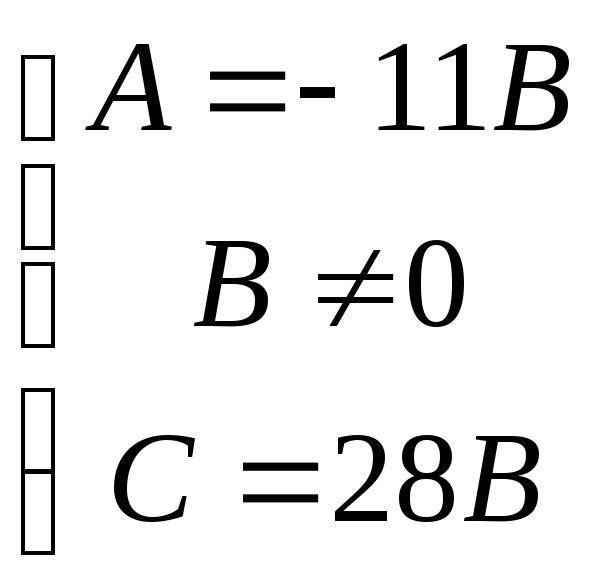
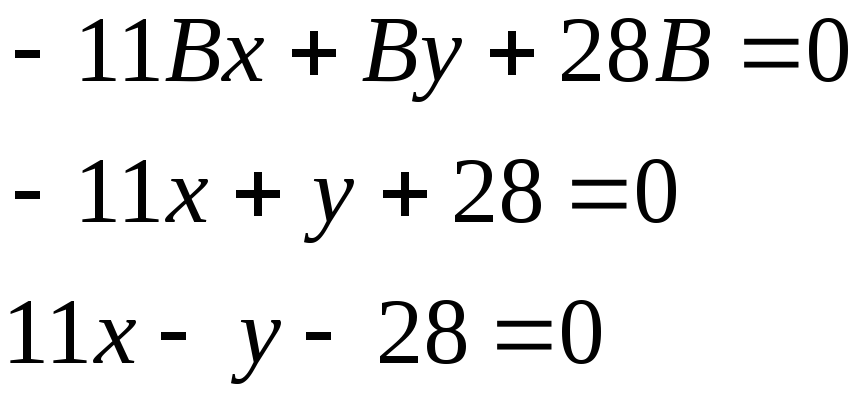
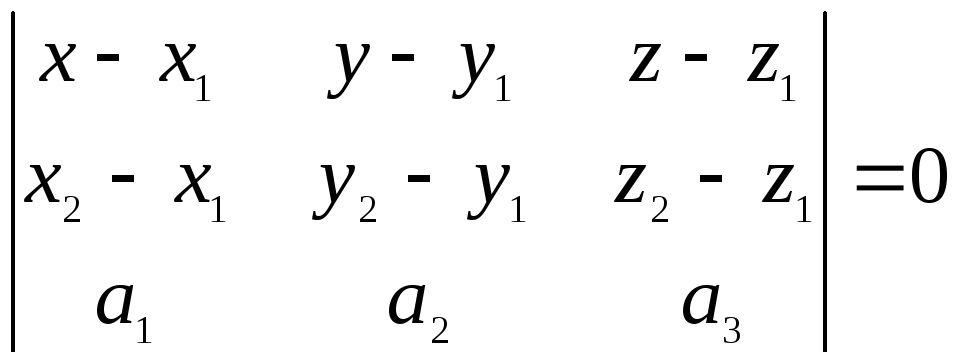 ,
,
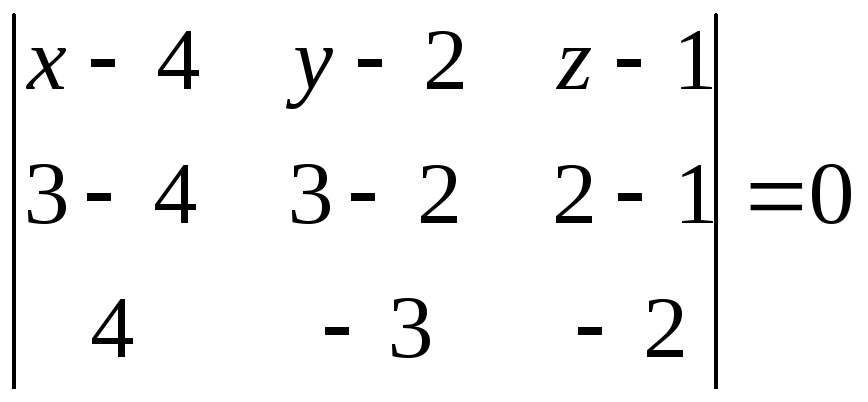 ,
,
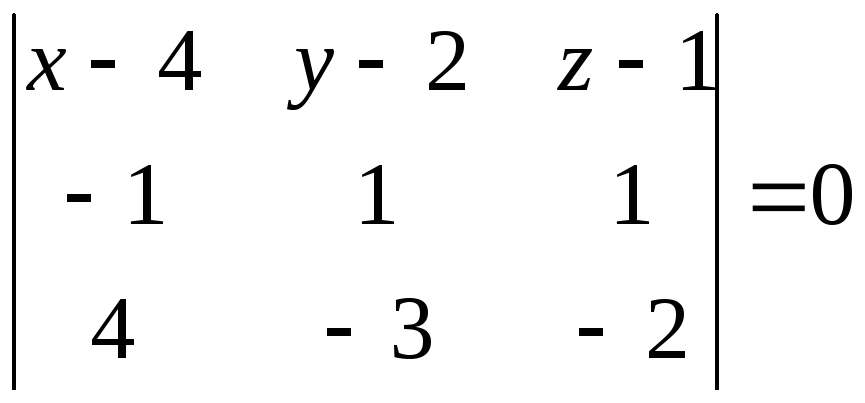
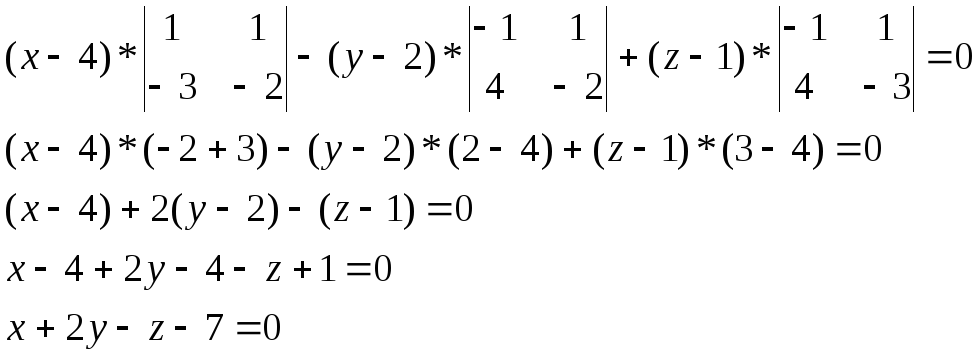
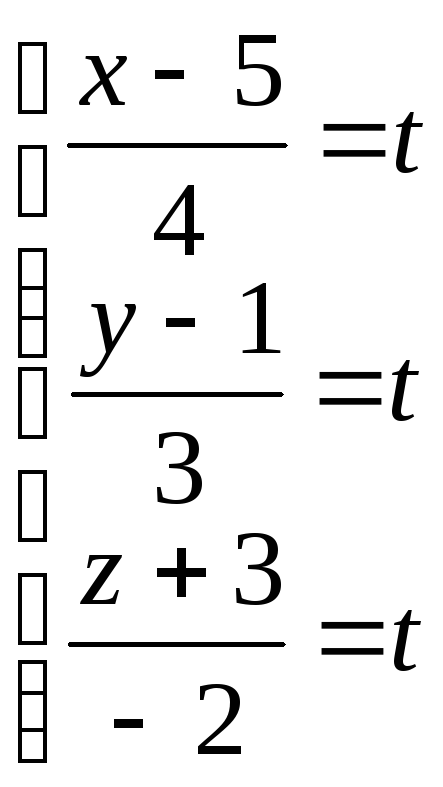
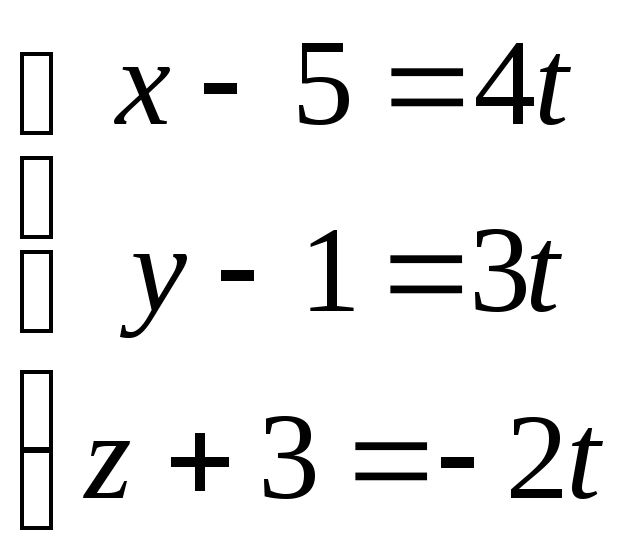
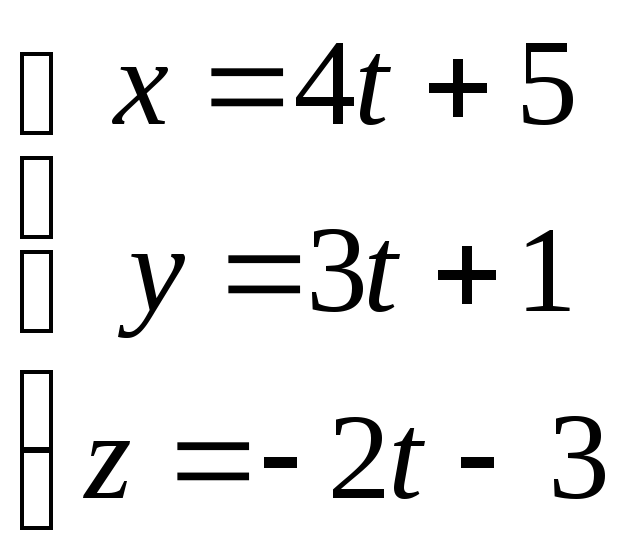
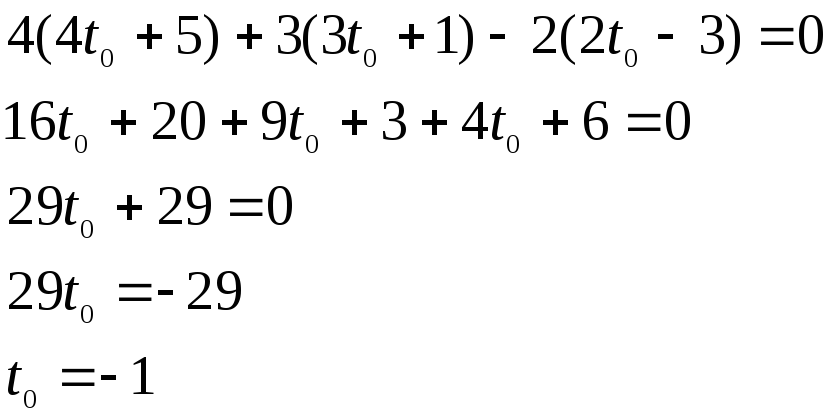
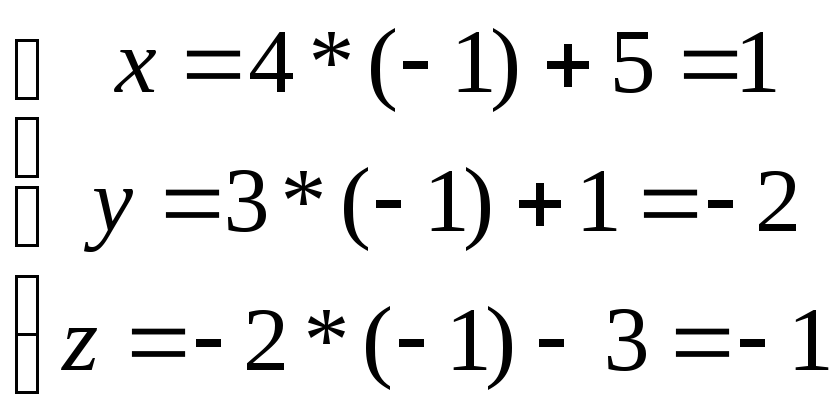
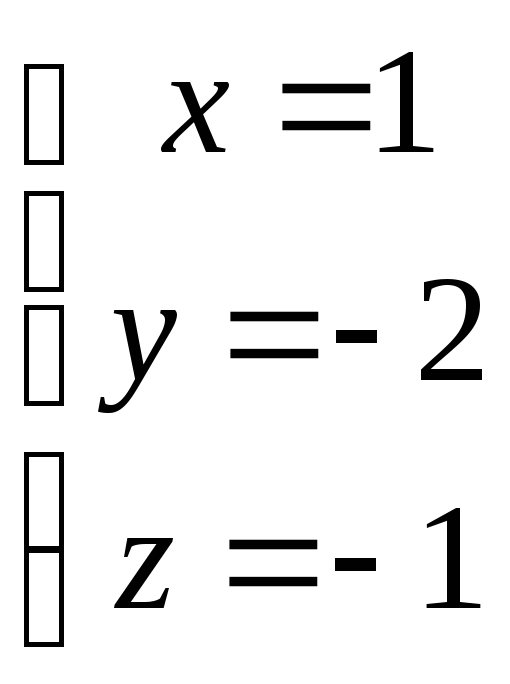
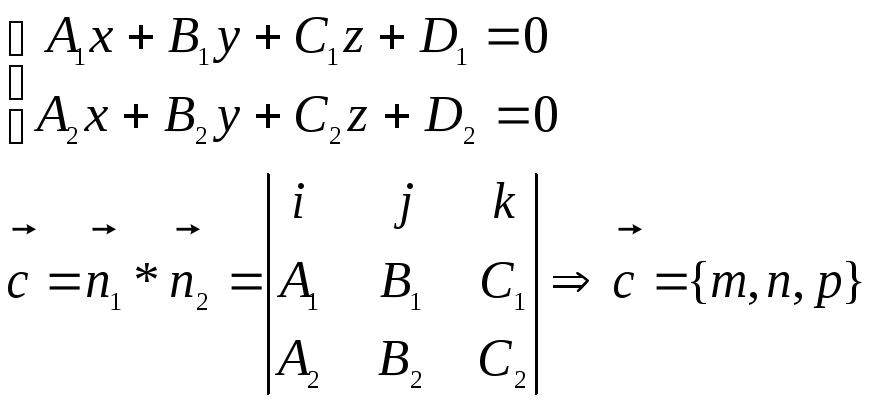
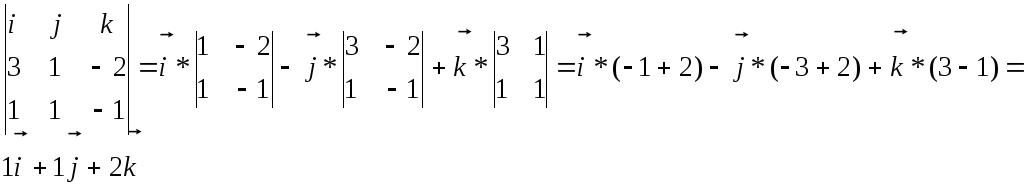
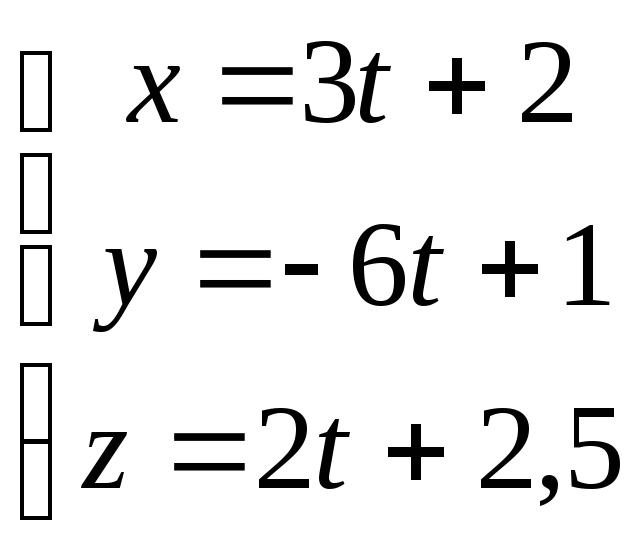 и найдём точку
пересечения её с плоскостью 3x-6y+2z+30=0
и найдём точку
пересечения её с плоскостью 3x-6y+2z+30=0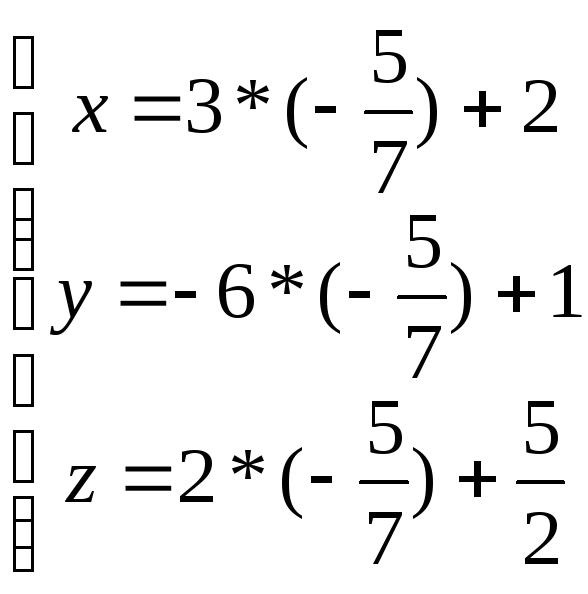
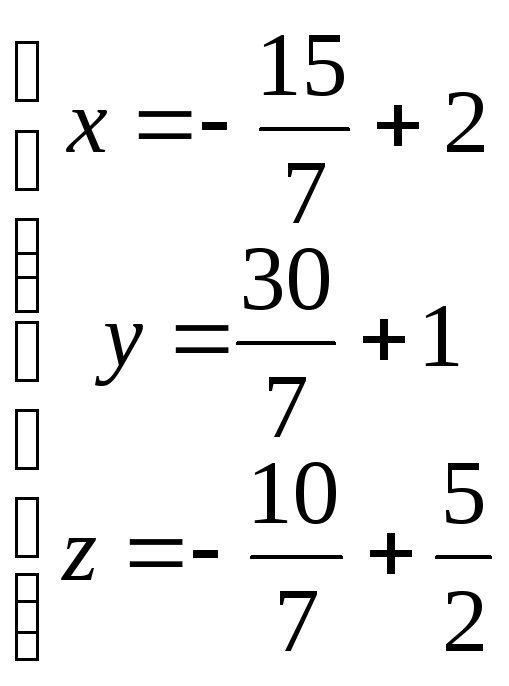
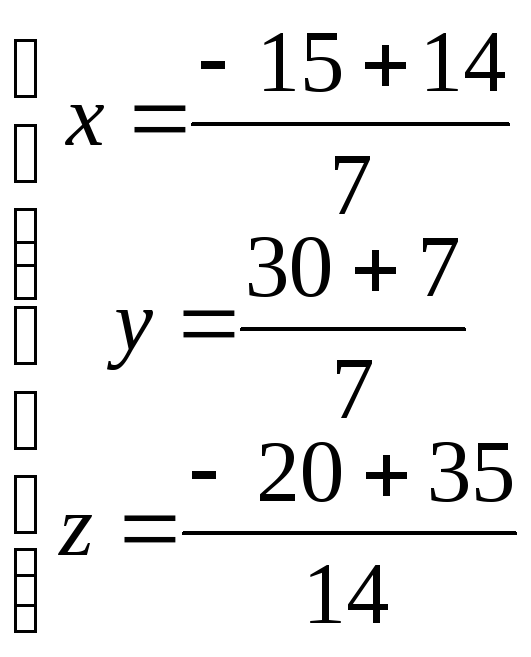
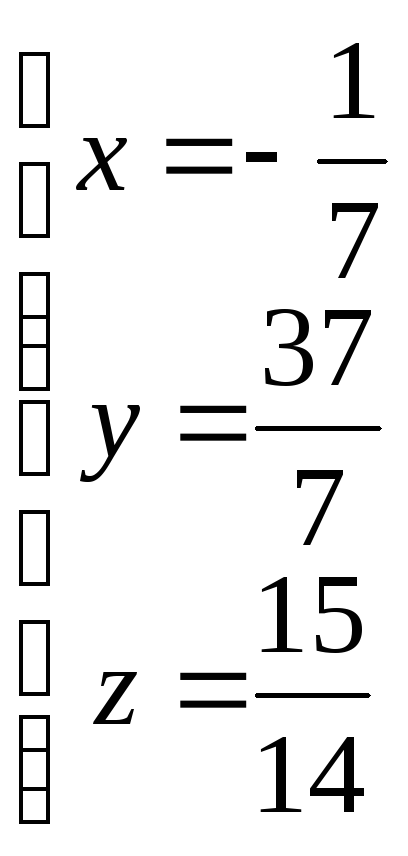
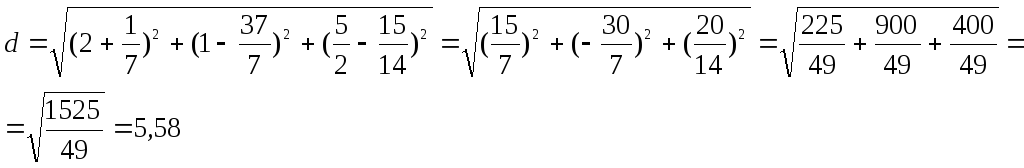
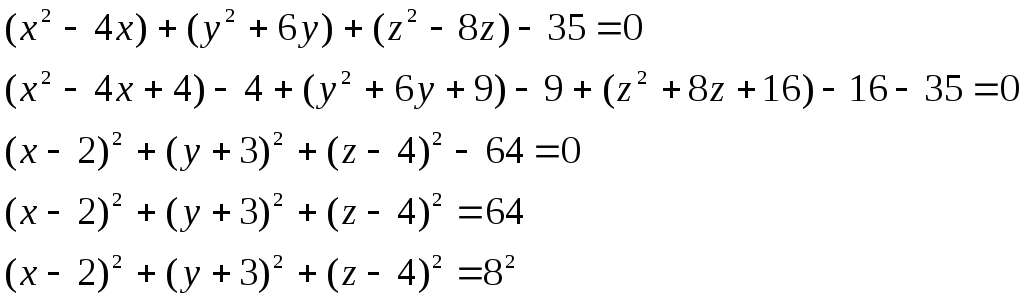
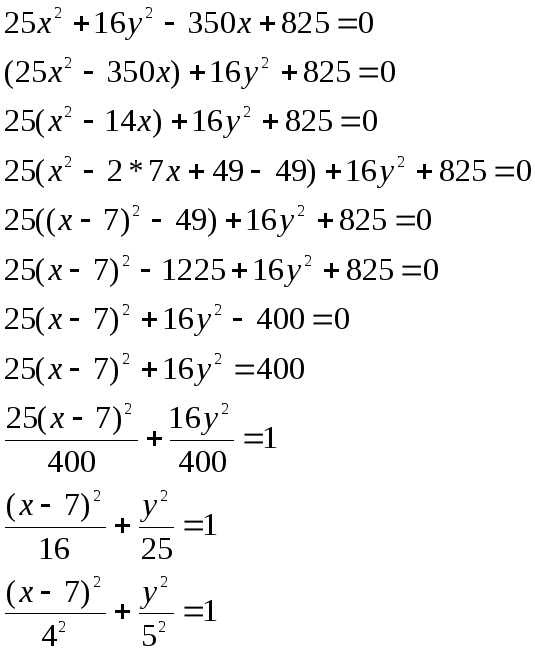
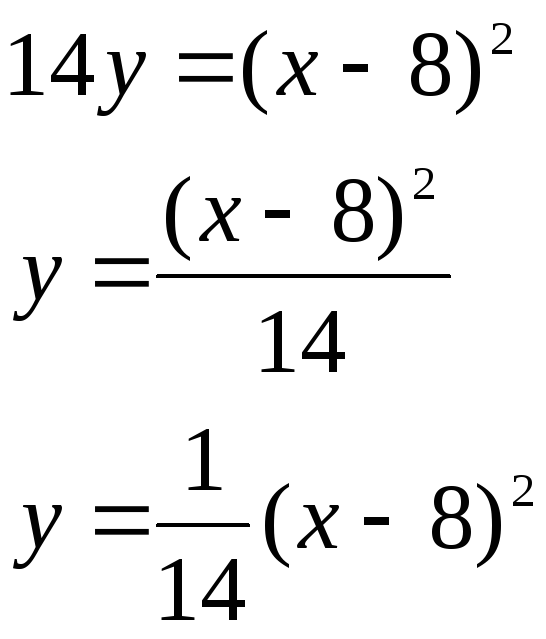

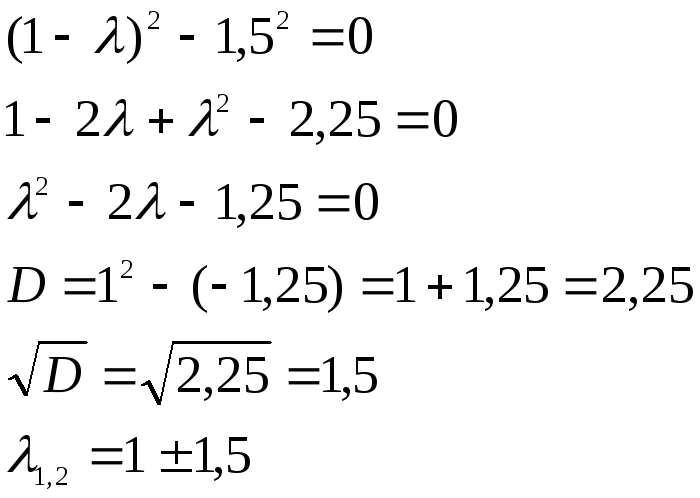
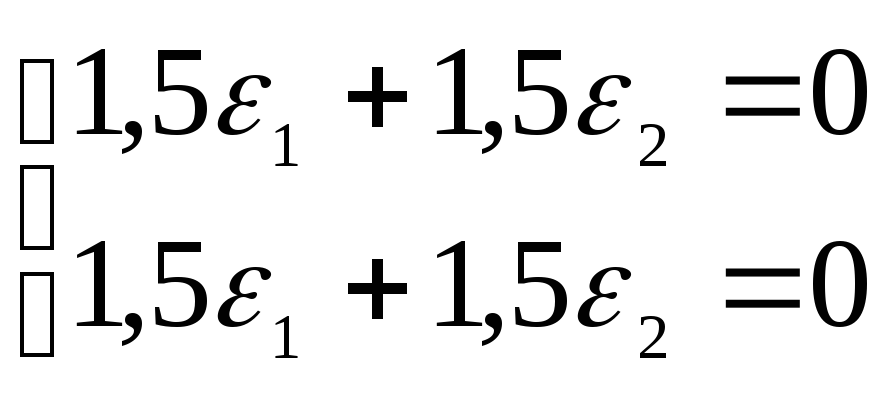 ,
отсюда получаем
,
отсюда получаем
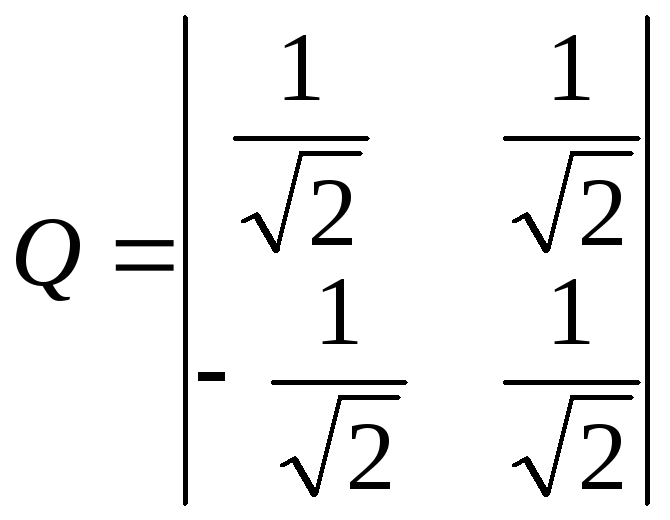 ,
,
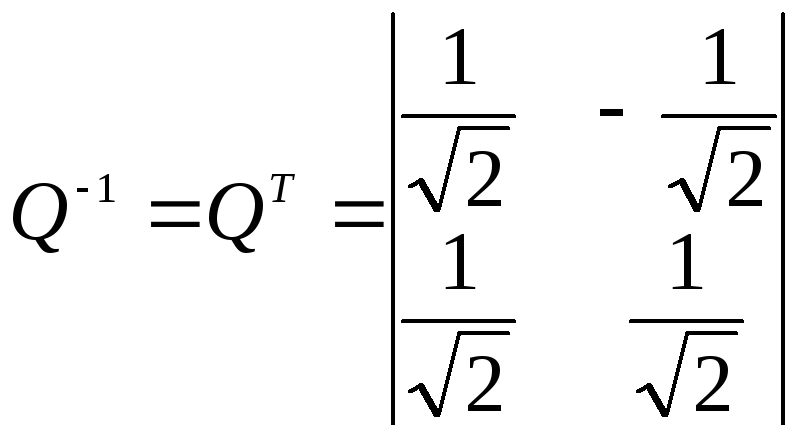
 ,
,
 или
или