Контрольная работа 2 / 2- 3_Высшая математика

Министерство высшего образования

РФ ТГУСУР.

Контрольная работа №2, по дисциплине

Высшая Математика №1.

Выполнил студент ТМЦ-ДО:

Ф.И.О.

К_Д – **********

П – **********

Принял:

Норильск 2002.

Вариант - (10*31) div 100 = 3

Задание №1.

Записать общее Ур-е прямой, проходящей через точку M(-2,4) перпендикулярно

прямой x + 2y + 5 = 0. Найти площадь треугольника, образованного данной прямой

с осями координат.

Решение:

а).

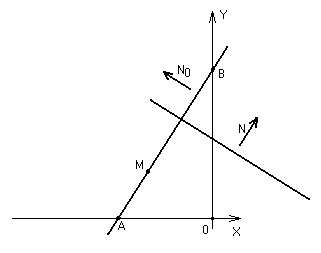
Найдём Ур-е прямой.

Т.к прямая перпендикулярна к прямой x + 2y + 5 = 0. =>

N(1,2) N(2,-1) =>

2x - y - (-4 + (-4)) = 0.

2x - y + 8 = 0. – Искомое Ур-е прямой.

б).

Найдём точки пересечения прямой с осями координат.

A(-4,0) B(0,8)

С точкой O(0,0) точки образуют треугольник ABO

Найдём его площадь.

BO=(0,-8) AO=(4, 0)

Ответ: 2x – y + 8 = 0 S = 16.

Задание №2.

Записать общее Ур-е прямой, проходящей через точку M(-2,2) и отсекающей от первого координатного угла треугольник площадью S = 4,5 кв. ед.

Решение:

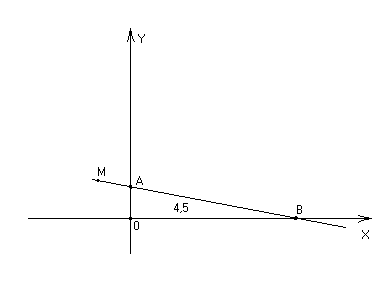
Будем искать уравнение прямой в виде y = kx + b т.к прямая проходит через точку

M(-2,2) то 2 = -2k + b;

Находим точки пересечения прямой с осями координат.

A( 0, b) AO( 0, -b)

B(-,0) BO(-,0)

Т.к то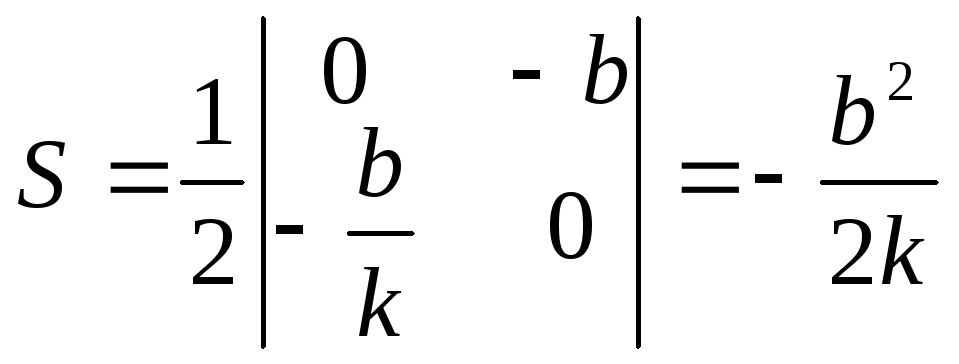

S = 4,5 = => =>

-b² – 9k = 0

Составим систему ур-й

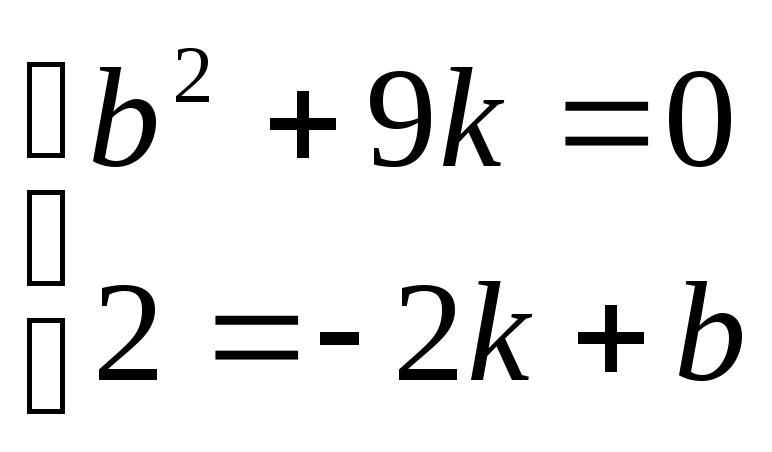
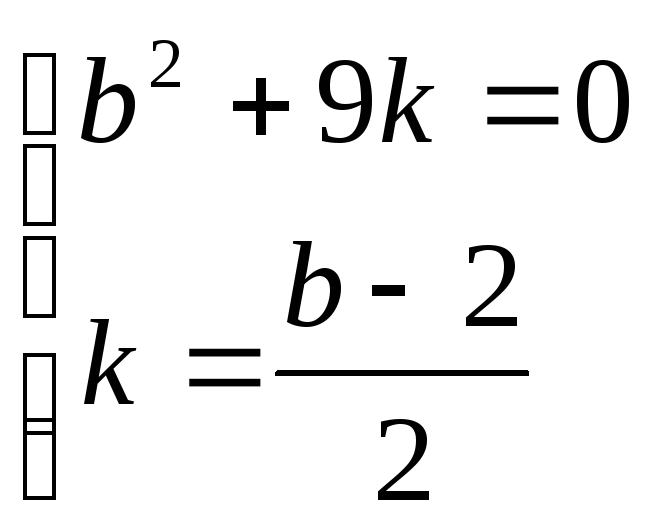
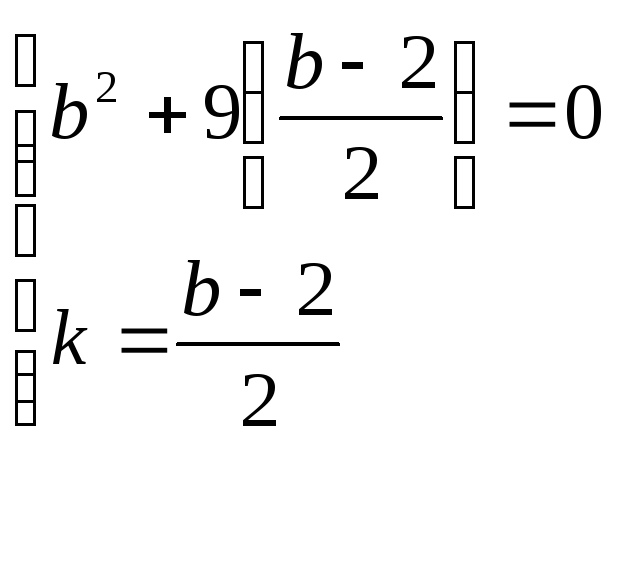
b² + 9b – 18 = 0

Решая это кв. Ур-е получим корни b₁ = - 6 b₂ = ; т.к b>0 то правильное

значение b₂ = подставив данное значение в Ур-е получим значение

для k = .

Подставив полученные значения b и k в Ур-е y = kx + b

найдём искомое Ур-е прямой :

Ответ: искомое Ур-е прямой .

Задание №3.

Даны вершины треугольника A(2,1,0), B(3,-1,1) и C(1,2,-4). Записать общее ур-е

плоскости, проходящей через сторону AB перпендикулярно плоскости треугольника ABC.

Решение:

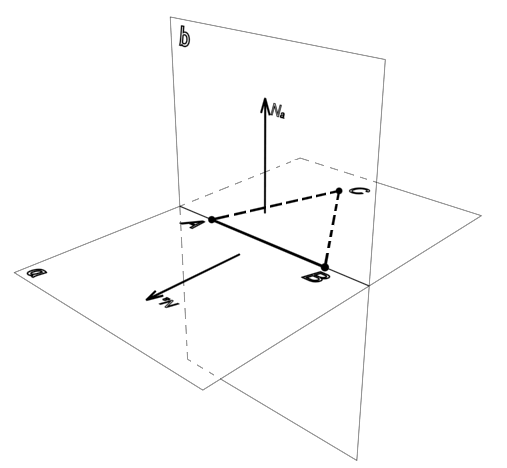
Плоскость ABC обозначим через α неизвестную через β.

Т.к

L₁ = AB( 1,-2,1)

L₂ = AC(-1,1,-4) то можно найти нормаль плоскости α

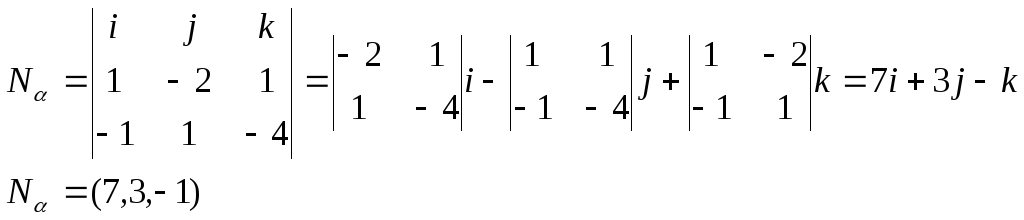
т.к пл β проходит через отрезок AB пл. α, то

L₁ = AB(1,-2, 1) т.к пл N_α || β, то

L₂ = N_α(7,3, -1)

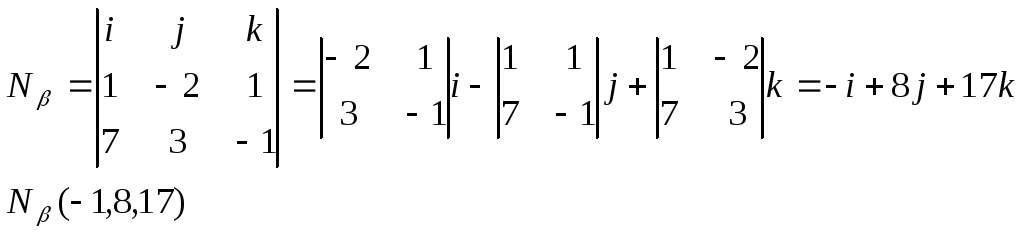
Зная нормаль и точку принадлежащую плоскости, можно найти ур-е плоскости

-x + 8y + 17z – (-2 + 8) = 0

x – 8y – 17z + 6 = 0

Ответ: искомое Ур-е прямой x – 8y – 17z + 6 = 0

Задание №4.

Найти расстояние от точки P(1,2,0) до прямой

Решение:

Расстояние от точки до прямой можно определить по ф-ле

r₁( 1, 2,0)

r₀(-8,-1,0)

l ( 3,-4,0)

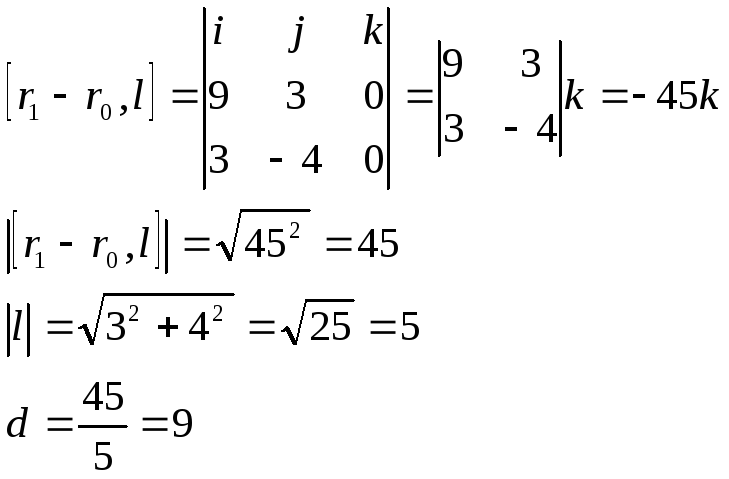
Ответ: d = 9

Задание №5.

Найти длину отрезка, отсекаемого от оси ординат плоскостью, которая проходит

через точку A(1,1,6) перпендикулярно вектору AB, где B – точка пересечения медиан треугольника, вершины которого совпадают с точками пересечения осей координат

с плоскостью 12x + 6y + z - 24 = 0.

Решение:

Обозначим известную плоскость через β, а неизвестную через α.

Для решения задачи потребуется найти Ур-е пл α .

Т.к пл α проходит через т A(1,1,6) AB то вектор AB можно принять

за нормаль плоскости α.

Найдём координаты точки B.

Для этого нужно найти точки пересечения плоскости β с координатными прямыми.

X(x,0,0) 12x - 24 = 0 X ( 2,0,0)

Y(0,y,0) 6y - 24 = 0 Y ( 0,4,0)

Z(0,0,z) z - 24 = 0 Z(0,0,24)

Найдём середины отрезков XY и YZ

D (1,2,0) K(0,2,12)

XK(-2,2,12) ZD(1,2,,-24)

M₁ (2,0,0) M₂ (1,2,0)

Исходя из найденных данных можно записать Ур-я медиан данного треугольника

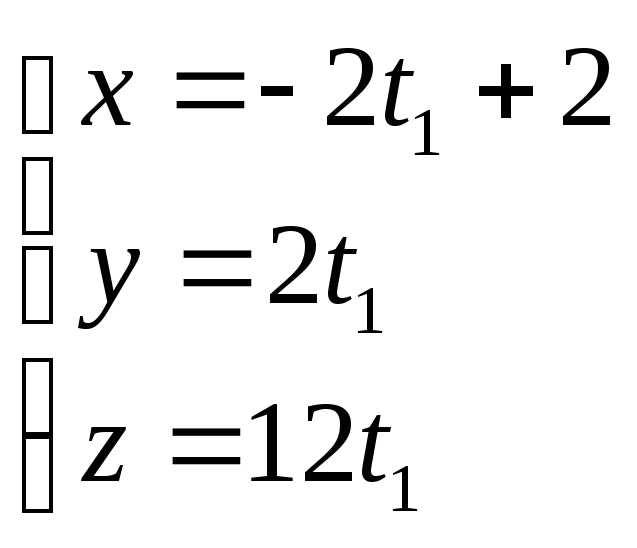
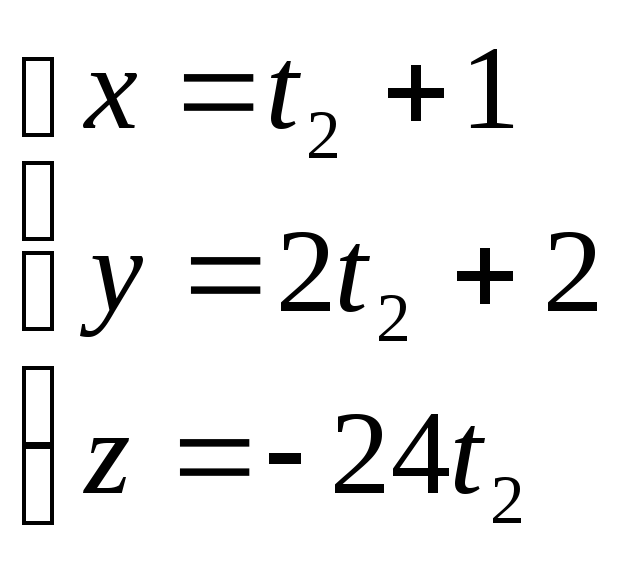
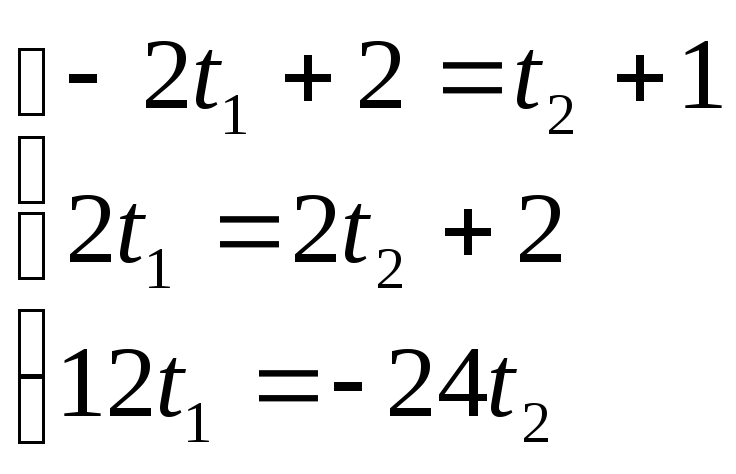
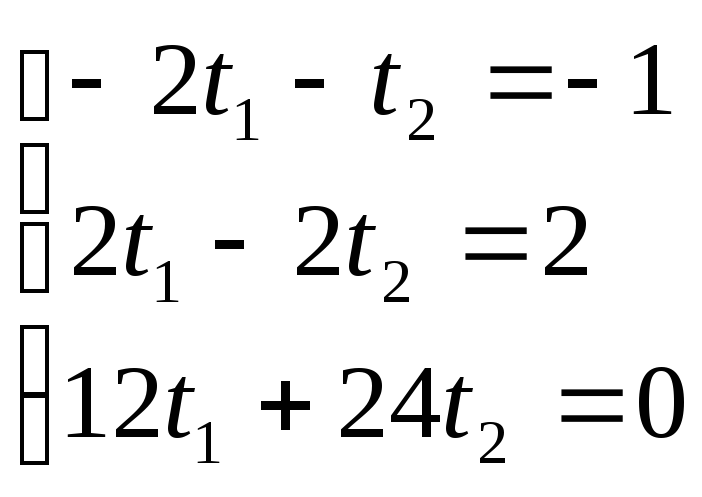
где базисный минор

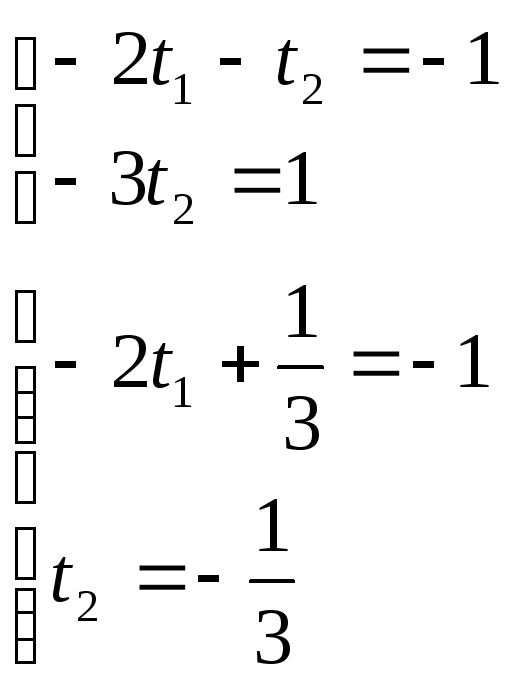
Подставив значения в любое уравнение медиан, можно найти их точку пересечения

Найдём отрезок AB

т.к нам известно координаты вектора нормали и точки лежащей на плоскости α

то можно определить Ур-е плоскости α

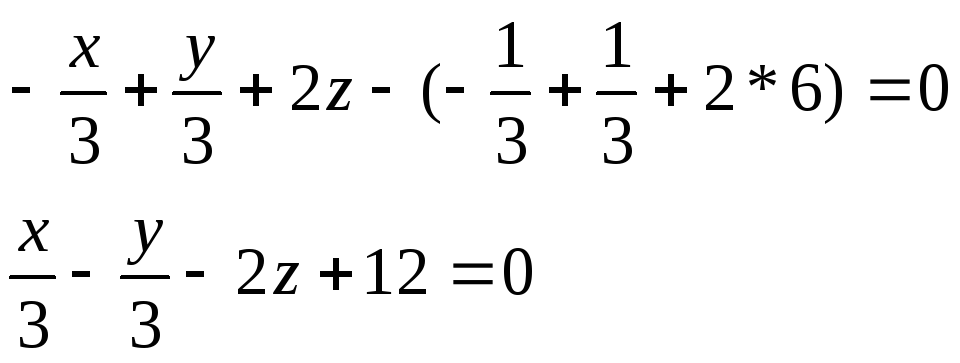
Теперь нужно найти точку пересечения плоскости с осью ординат (0,y,0)

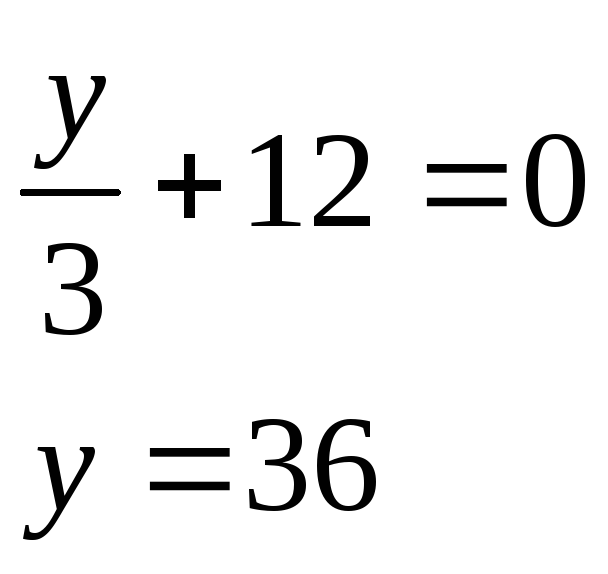
C(0,36,0) O(0,0,0)

OC(0,36,0)

Ответ: Длина отрезка d = 36.

Задание №6.

Две прямые параллельны плоскости 4x + 3y + 6 z = 0 Первая прямая проходит через точку P(1,2,3) и пересекает ось абсцисс, а вторая – через точку Q(3,0,0) и пересекает ось ординат. Найти Косинус угла между направляющими векторами прямых.

Решение:

Одна прямая проходит через точки P(1,2,3) и M₁(0,a,0)_, а вторая через точки Q(3,0,0) и M₂(b,0,0) Вектора PM­₁ и QM₁ являются направляющими векторами прямых.

L₁=PM₁(-1,a - 2,-3)

L₂=QM₂(b – 3,0,0)

Векторы PM₁ и QM₂ вектору нормали заданной плоскости

N₀ (4,3,6) отсюда:

(L₁,N₀) = 0; -4 + 3(a - 2) – 18 = 0

-4 + 3a – 6 – 18 = 0 a =

(L₂,N₀) = 0; 4(b - 3) = 0 b = 3

L₁ (-1,,-3) L₂ (0,0,0)

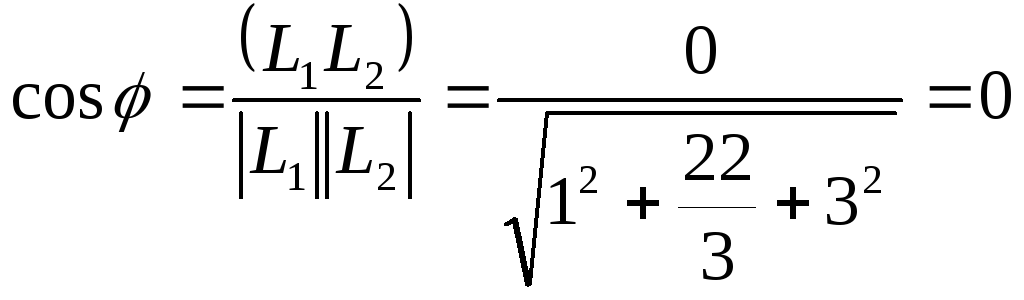
Ответ: cosφ = 0;

Задание №7.

Найти координаты центра C(x₀ , y₀) окружности радиусом 5, касающейся

прямой 3x + 4y - 6 = 0 в точке M(2,0), если известно что точка C находится в первой четверти.

Решение:

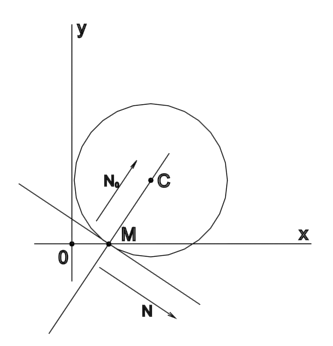
Для нахождения центра окружности необходимо найти параметр D (D = Ax₀ + By₀ ) прямой B проходящей через точки M и C. Данная прямая перпендикулярна прямой 3x + 4y – 6 = 0 которая является касательной к окружности.

N₀(3,4) => N(4,-3)

Найдём уравнение прямой B с точкой M(2,0)

D = (4x₀ - 3y₀) = 8

4x – 3y – 8 = 0 значит параметр D в точке C

4x₀ – 3y₀ = 8

Для составления системы ур-й потребуется так же и Ур- е окружности

(x - x₀)²+(y – y₀)² =r² r = |MC| = 5 M(2,0)

(2 – x₀)²+(0 – y₀)² = 25

Составим систему Ур-й

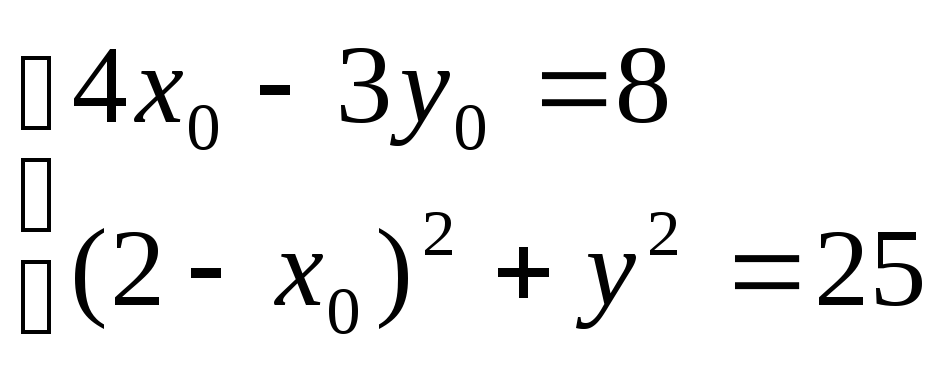
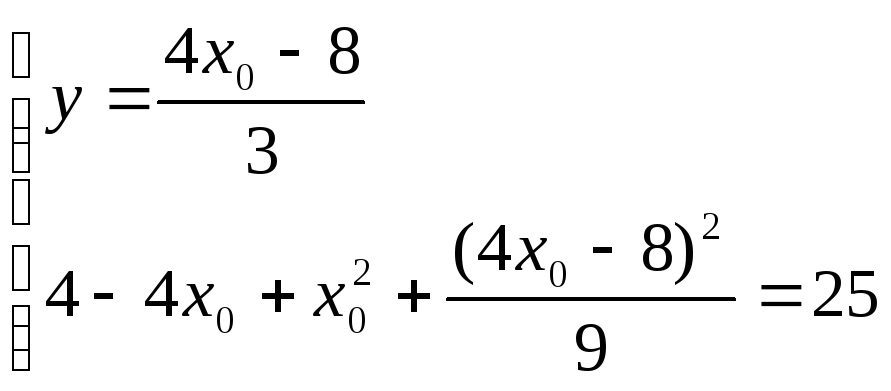
решаем кв. Ур-е x

D = (-4)² – 4(-5) = 36

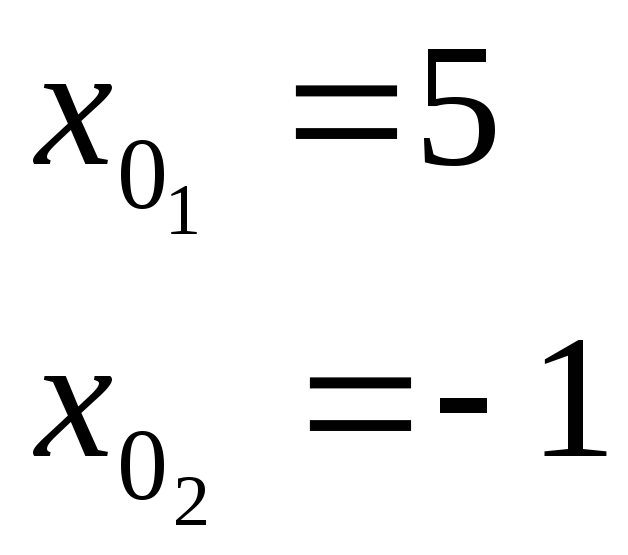
По условию точка C лежит в I ч-ти найдём y₀

Ответ: С (5,4)

Задание №8.

Дана кривая 9x² – 4y² – 18x + 56y – 223 = 0

1.Доказать что эта кривая – гипербола.

2.Найти координаты её центра симметрии.

3.Найти действительную и мнимую полуоси.

4.Записать Ур-е фокальной оси.

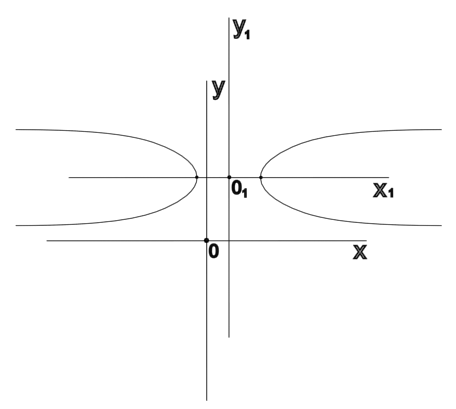5.построить данную кривую.

Решение:

Выделяя полные квадраты, данное Ур-е можно записать в виде 9(x – 1)² – 4(y – 7)² = 36

или положим x₁ = (x – 1) y₁ = (y – 7)

Тогда Данная кривая – гипербола с центром в точке

x – 1 = 0 y – 7 = 0 т.е. в точке (1,7) и её действительная полуось, а

мнимая.

Фокальная ось y – 7 = 0

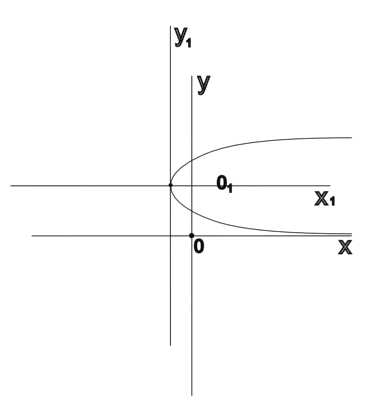
Задание №9.

Дана кривая x² + 2x – 2y + 5 = 0

1.Доказать что эта кривая – парабола.

2.Найти координаты её вершины.

3.Найти значение её параметра p.

4.Записать Ур-е её оси симетрии.

5.построить данную кривую.

Решение

Выделяя полные квадраты, данное Ур-е можно записать в виде (x + 1)² – 2(y – 2) = 0

Положив x₁ = (x + 1) y₁ = (y – 2) тогда

её параметр 2p = 2 p = 1

Вершина находиится в точке x + 1 = 0 y – 2 = 0 т.е в точке (-1,2)

Ось симметрии y – 2 = 0