Министерство образования

Российской Федерации

ТОМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

СИСТЕМ УПРАВЛЕНИЯ И РАДИОЭЛЕКТРОНИКИ (ТУСУР)

Кафедра высшей математики

Контрольная работа №2

Аналитическая геометрия

2000

1. Записать общее уравнение прямой, проходящей через точку М(2,-3) параллельно вектору АВ, если А(4,5), В(3,-7).

Найдем координаты вектора АВ: =(-1,-12)

, где n, m – координаты вектора параллельно строящейся прямой.

Подставляя данные в уравнение получим общее уравнение прямой:

-12x+24=-y-3 -12x+y+27=0

ОТВЕТ: общее уравнение прямой -12x+y+27=0

2. Стороны треугольника АВС заданы уравнениями: и . Записать общее уравнение высоты АН.

(1.1)

Находим координаты точки А

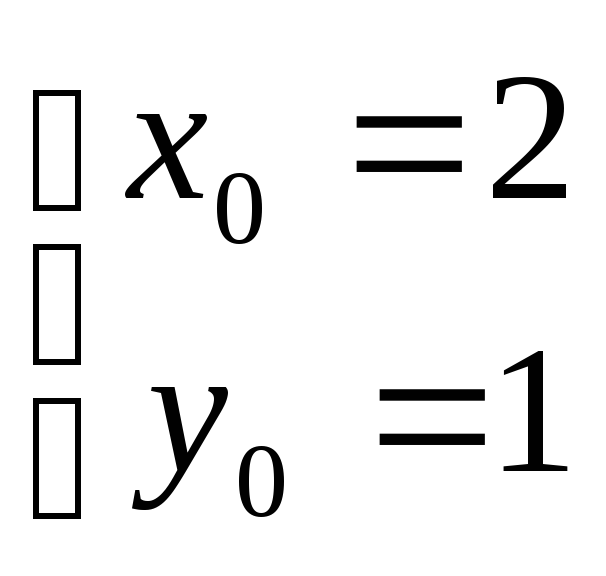Согласно формуле (1.1)

ОТВЕТ: общее уравнение высоты АН

3. Записать общее уравнение плоскости, проходящей через точки М₁(3,0,4) и М₂(1,1,0) перпендикулярно плоскости 2x+y+4z-7=0.

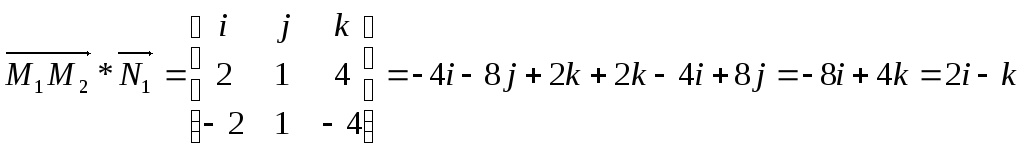
ОТВЕТ: уравнение плоскости 2x-z-2=0

4. Найти расстояние от точки Р(2,4,4) до прямой

3x=3

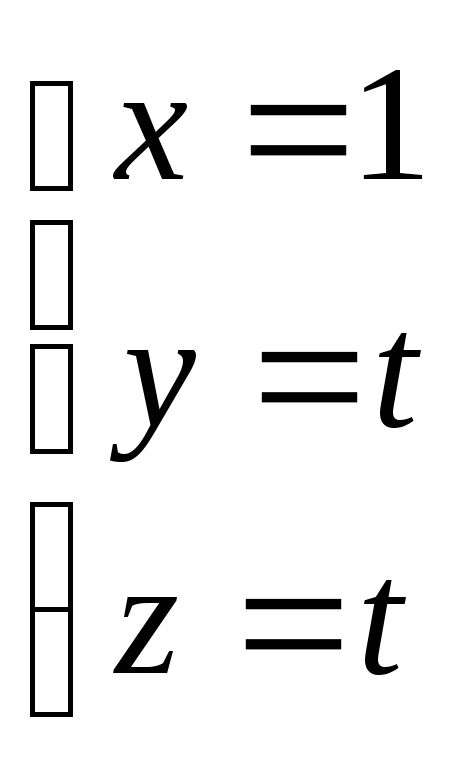
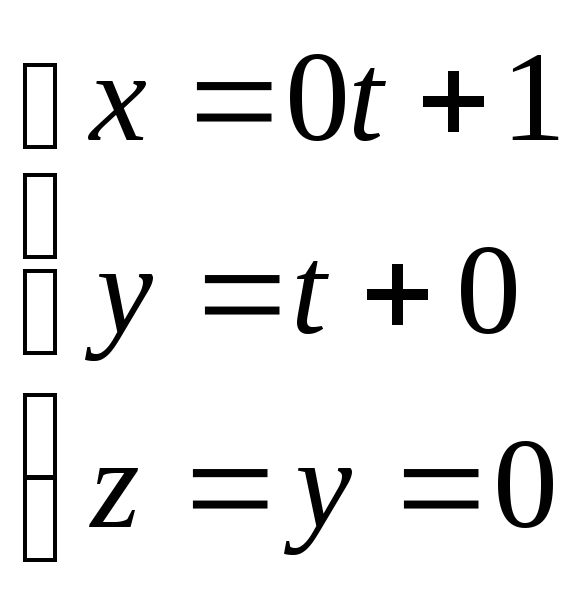
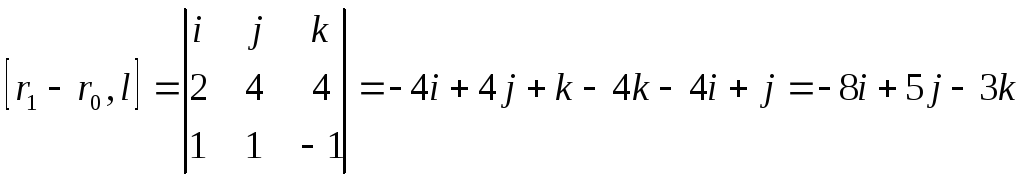
ОТВЕТ: расстояние от точки Р(2,4,4) до прямой равно

5. Плоскость проходит через прямую паралельно вектору АВ=(8,4,7). Найти длину отрезка, отсекаемого этой плоскостью от оси ординат.

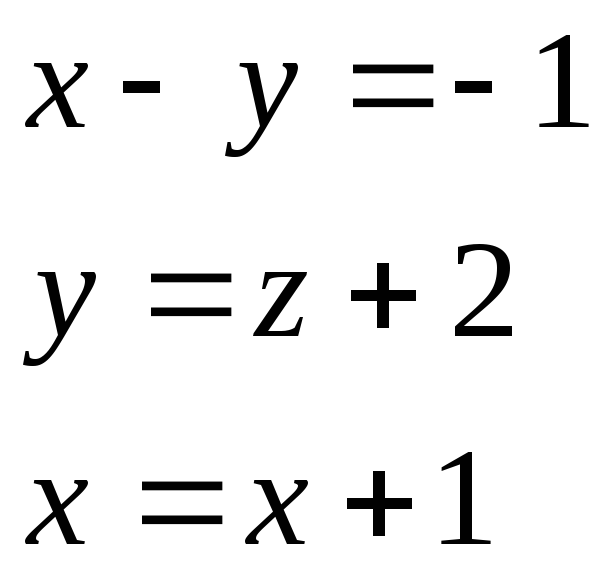
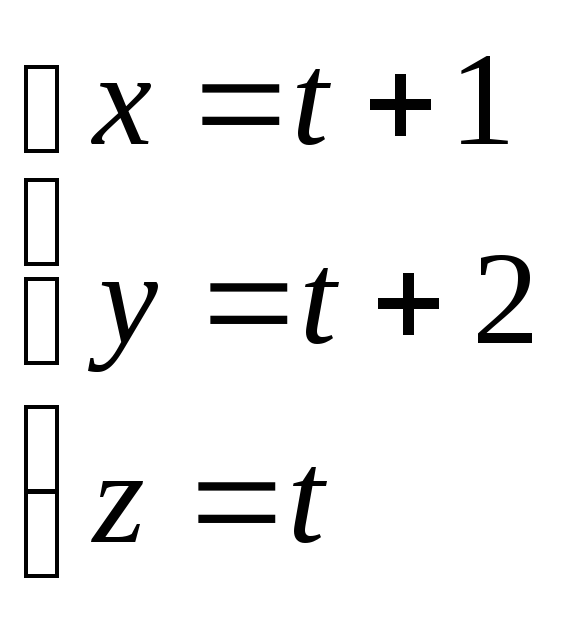
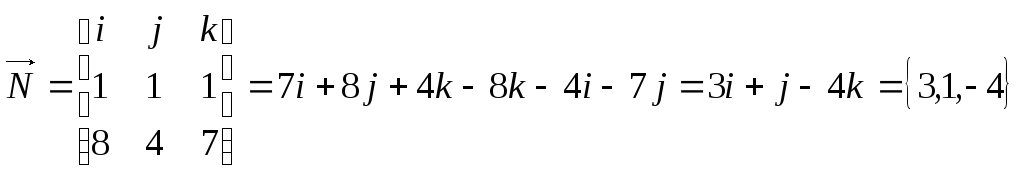
Найдем т. О плоскости

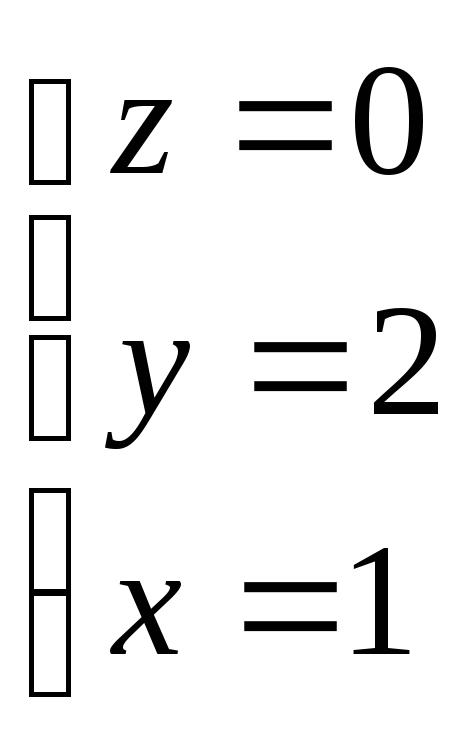
- ур-е плоскости

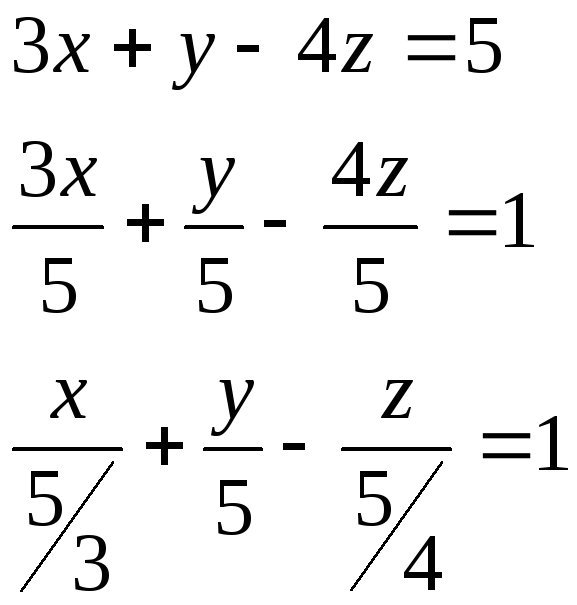
ОТВЕТ: длина отрезка равна 5.

6. Две прямые, пересекающиеся в точке Р(0,0,z₀), z₀>0 параллельны плоскости 2х + у + 2z + 6=0 и отстоят от неё на расстоянии 4. Одна из прямых пересекает ось абсцисс, а вторая — ось ординат. Найти тангенс острого угла между ними.

- точки пересечения оси x

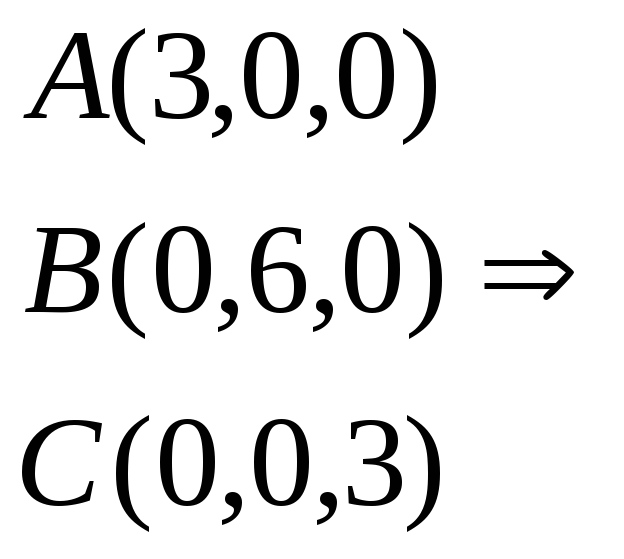
О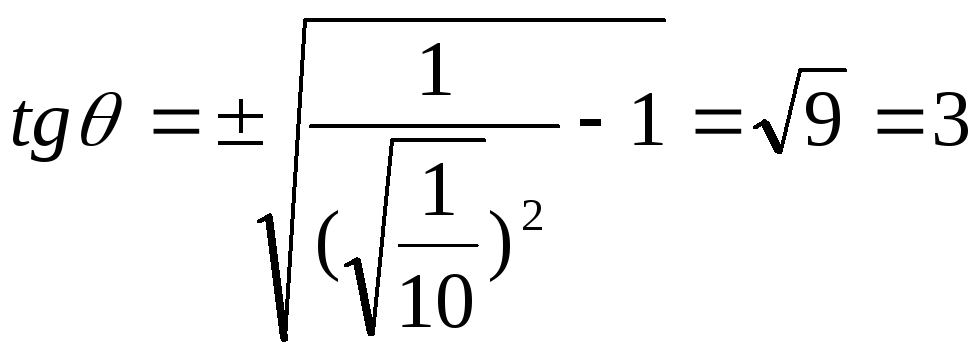 ТВЕТ: тангенс острого угла равен 3.

7. Найдите радиус окружности с центром в точке M(2,4), если известно, что прямая Зх + 4у+8 = 0 касается этой окружности.

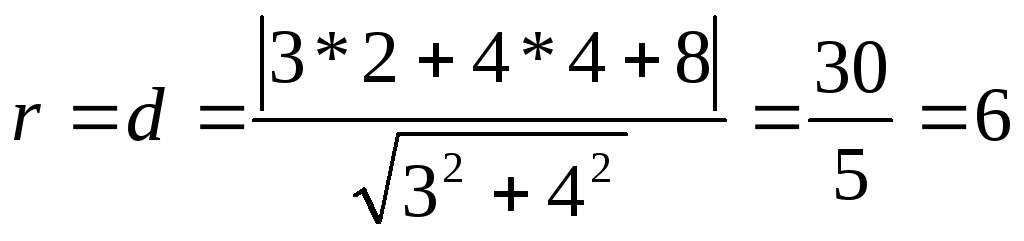
8. Дана кривая 25x2 + 16у2 - 150х - 32у - 159 = 0.

8.1. Доказать, что эта кривая — эллипс.

8.2. Найти координаты центра его симметрии.

8.3. Найти его большую и малую полуоси.

8.4. Записать уравнение фокальной оси.

8.5. Построить данную кривую.

8.1

- эллипс

8.2

Центр симметрии О(-3,-1)

8.3

малая полуось в=5

8.4

F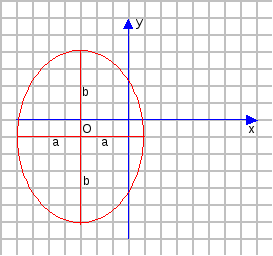 ₁(-7,-1); F₂(1,-1) – фокусы

8.5

9. Дана кривая у² - 2у + 4х + 9 = 0.

9.1. Доказать, что данная кривая — парабола.

9.2. Найти координаты её вершины.

9.3. Найти значение её параметра р.

9.4. Записать уравнение её оси симметрии.

9.5. Построить данную параболу.

9.1

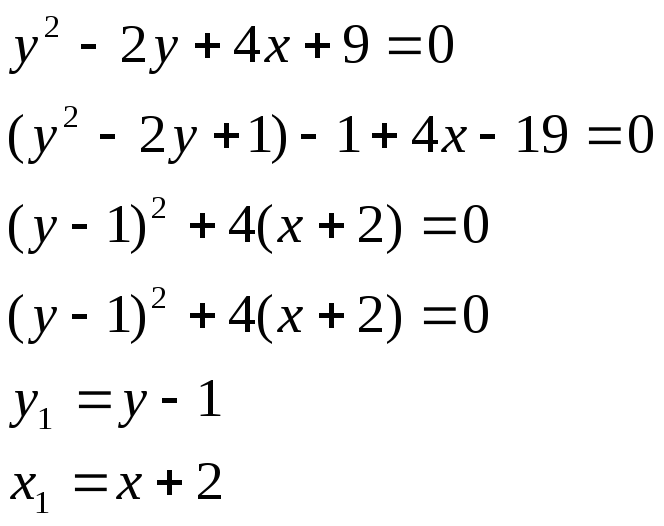
- парабола

9.2

O(-2,1)

9.3

9.4

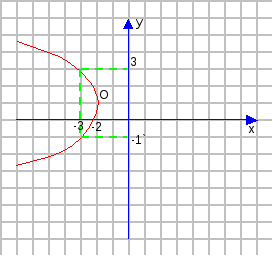9.5

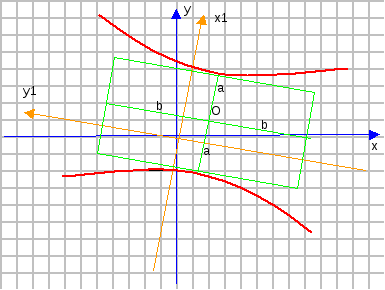
10. Дана кривая х2 - 7y2 - 6ху + 2х + 26у + 57 = 0.

10.1. Доказать, что эта кривая — гипербола.

10.2. Найти координаты её центра симметрии.

10.3. Найти действительную и мнимую полуоси.

10.4. Записать уравнение фокальной оси.

10.5. Построить данную гиперболу.

A

B

C

D

E

F

10.1

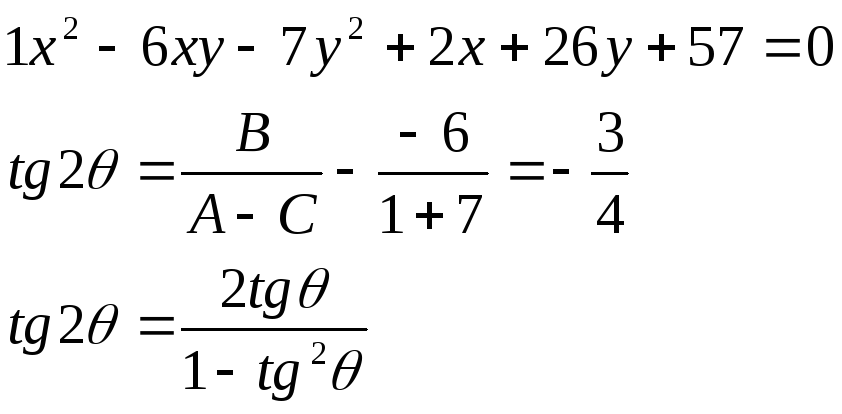
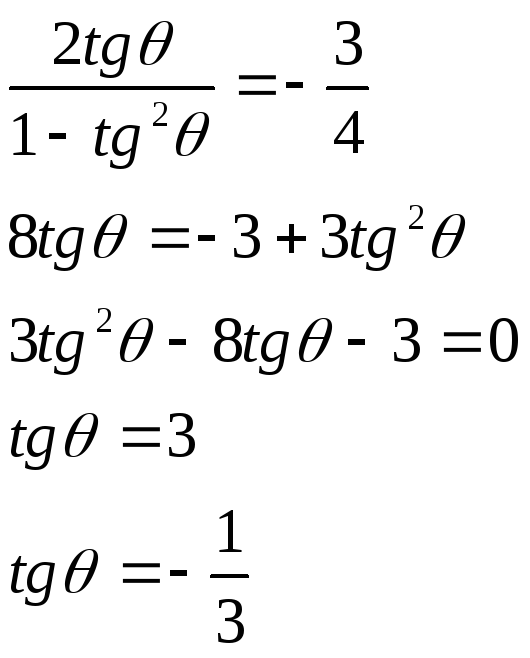
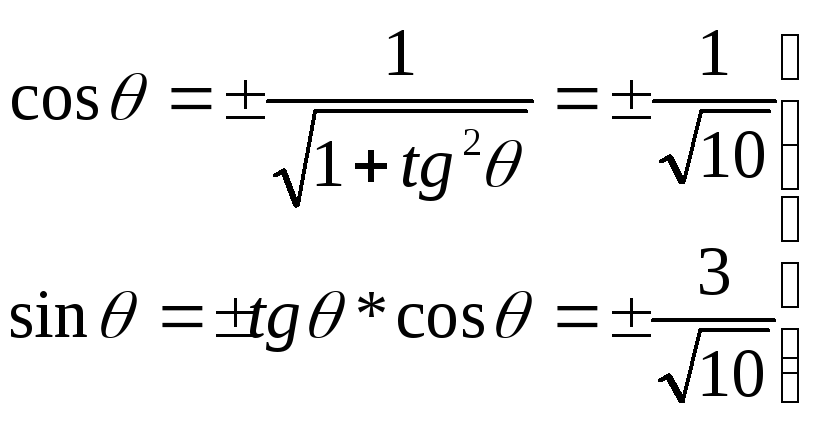пусть

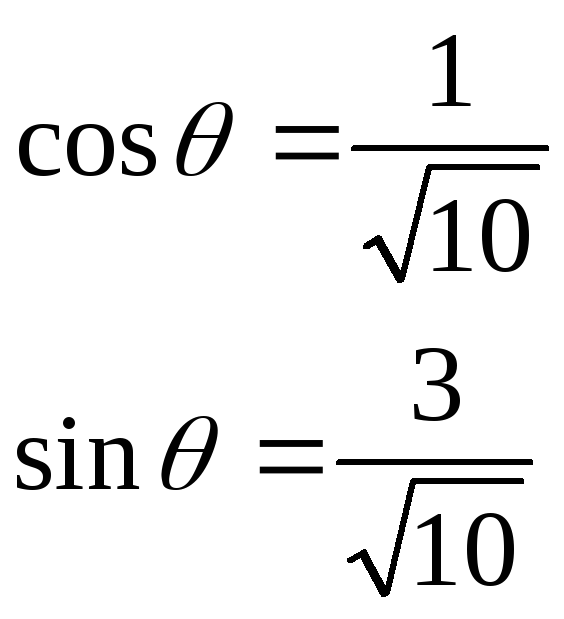
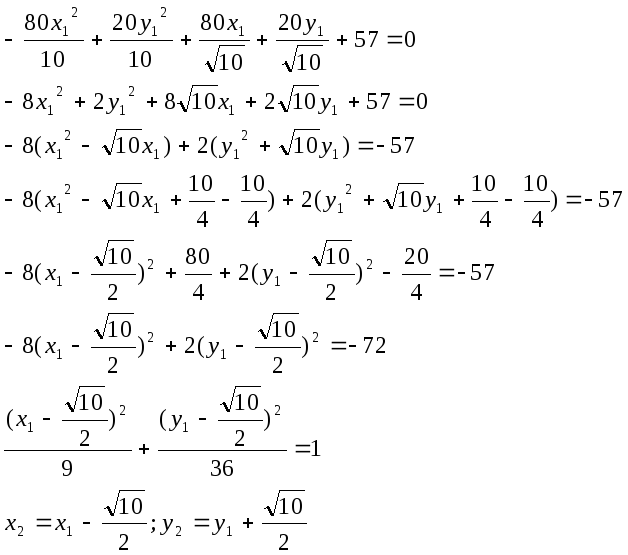
- гипербола

10.2

- центр симметрии в координатах o₁x₁y₁

в координатах oxy т.О имеет координаты :

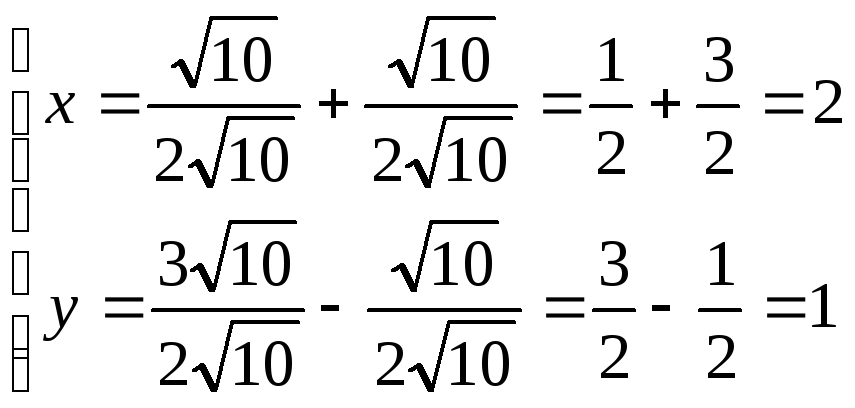
10.3

a=3

b=6

10.4

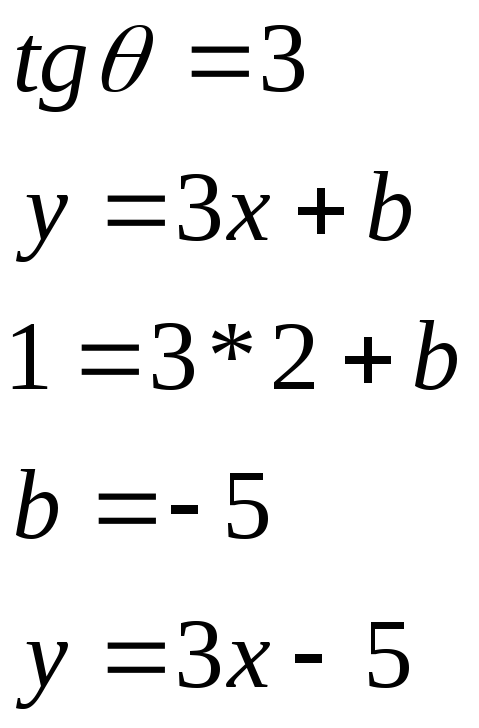
10.5