Контрольная работа 2 / 2- 2_Высшая математика_7

Министерство образования

Российской Федерации

ТОМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

СИСТЕМ УПРАВЛЕНИЯ И РАДИОЭЛЕКТРОНИКИ (ТУСУР)

Автоматизированная система обработки информации и управление

Высшая математика 1.

контрольная работа №2.

вариант№2.

Студент гр.

31.01.02

2002

Задача №1.

Записать общее уравнение прямой, проходящей через точку М₀(2,-3) параллельно вектору АВ , если А(4,5),В(3,-7).

Решение:

Найдём координаты вектора

=(3-4,-7-5)=(-1,-12)

Так как искомая прямая параллельна вектору , а потому вектору (12,-1), который можно принять в качестве вектора нормали прямой. Запишем искомое уравнение:

12х-у-(12*2+(-1)*(-3))=0  12х-у-27=0

Ответ: 12х-у-27=0 уравнение прямой проходящей через т. М₀(2,-3) параллельно АВ.

Задача №2.

Стороны треугольника АВС заданы уравнениями АВ: 4х-у-7=0; ВС: х+3-31=0; АС: х+5у-7=0. Записать общее уравнение высоты АН.

Решение:

Найдём координаты точки A, решив систему уравнений B

;;

H

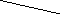
; A

C

;

АН ВС К_АН* К_ВС = -1, К_ВС = -1/3, К_АН = -1/К_ВС = 3.

Уравнение АН найдём по формуле

У-У_А = К_АН* (Х-Х_А) или У-1 =3*(Х-2), У-1 =3Х-6, 3Х-У-5 =0.

Ответ: 3Х-У-5 = 0 уравнение высоты АН.

Задача №3

Записать общее уравнение плоскости, проходящей через точки М₁(3,0,4) и М₂(1,1,0) перпендикулярно плоскости 2х+у+4z-7 = 0.

Решение:

Так как искомая плоскость к данной плоскости, то она параллельна векторам М₁ и М₂. Поэтому уравнение плоскости можно записать в виде:

; ; 



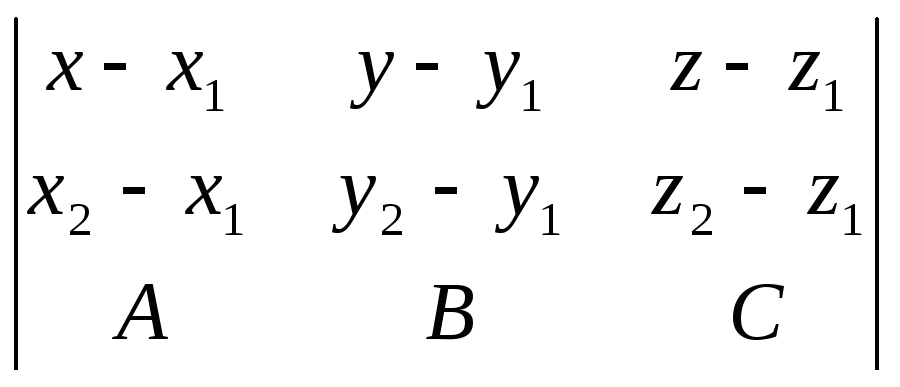
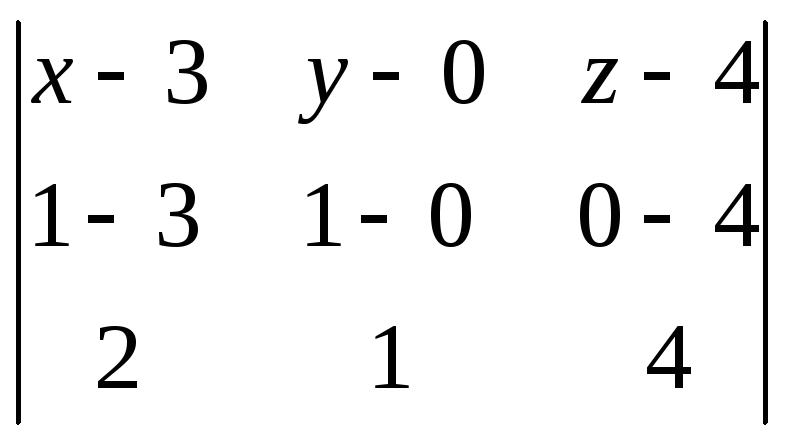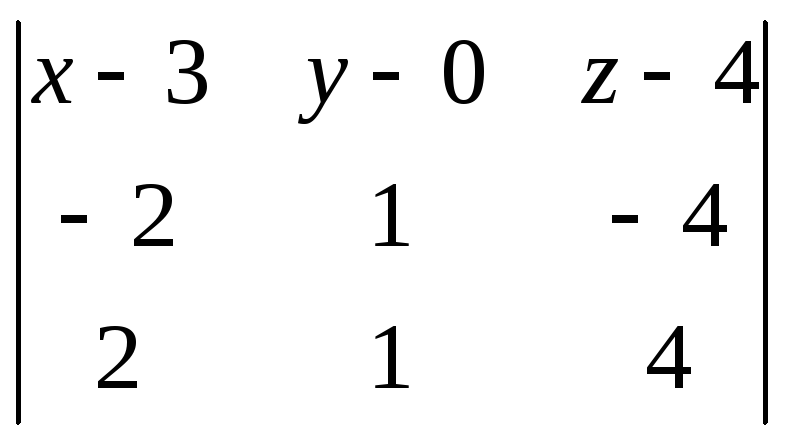
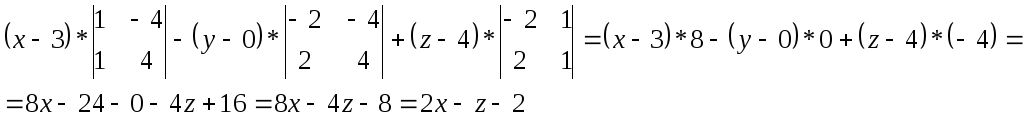
Ответ: – уравнение искомой плоскости.

Задача № 4.

Найти расстояние от точки Р(2,4,4) до прямой

Решение:

Найдём проекцию точки Р на прямую L. Проекцию Q найдём как точку пересечения прямой L с плоскостью П, проходящей через точку Р прямой L. Запишем параметрическое уравнение прямой L. Так как

, то неизвестное z можно принять в качестве свободного системы. Положим z=t и выразим из системы неизвестные х и у через t.



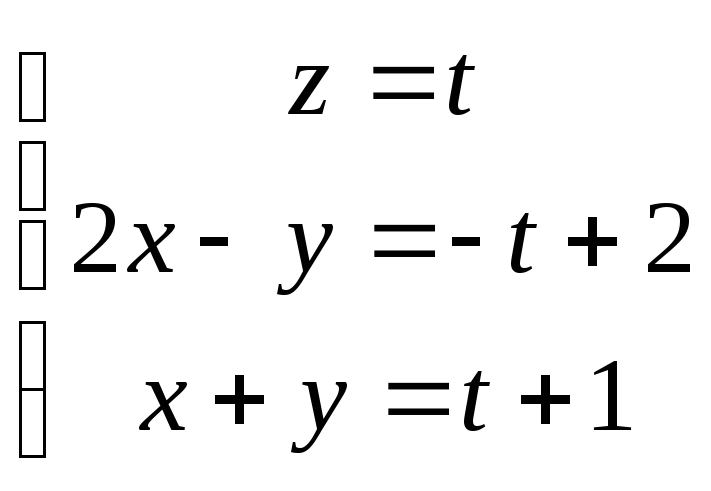
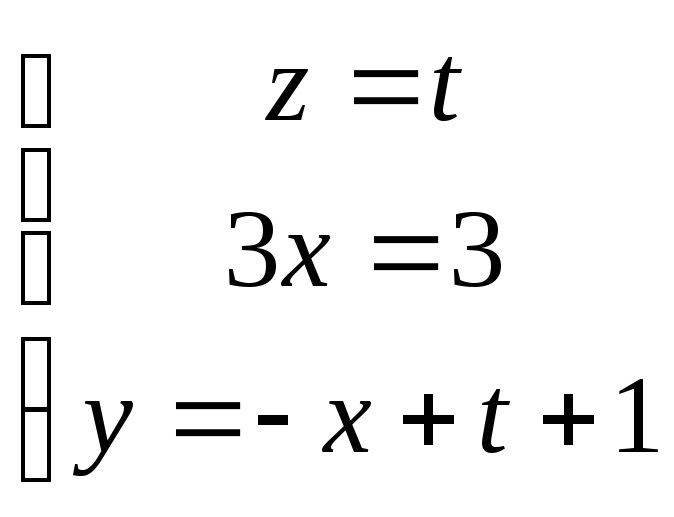
Параметрическое уравнение данной прямой. Направляющий вектор (0,1,1) можно принять в качестве вектора нормали плоскости П. Запишем уравнение плоскости П:

У + Z + D = 0, 4 + 4 + D = 0 (поскольку точка Р лежит в плоскости П), D = -8.

У + Z – 8 = 0 – уравнение плоскости П.

Находим точку пересечения прямой с плоскостью П и координаты точки Q:

t + t – 8 = 0, 2t = 8, t = 4. Q (1,4,4)

искомое расстояние найдём как длину отрезка

= Р(2,4,4)

== 1

Ответ: =1 Q

Задача №5.

Плоскость проходит через прямую

параллельно вектору АВ=(8,4,7). Найти длину отрезка, отсекаемого этой плоскостью от оси ординат.

Решение:

Плоскость П параллельна направляющему вектору прямой и вектору , поэтому вектор =[] является вектором нормали.

Найдём вектор .

Разрешив данную систему относительно X и Z(У- свободное неизвестное), получим

Пологая у = t, запишем параметрическое уравнение прямой

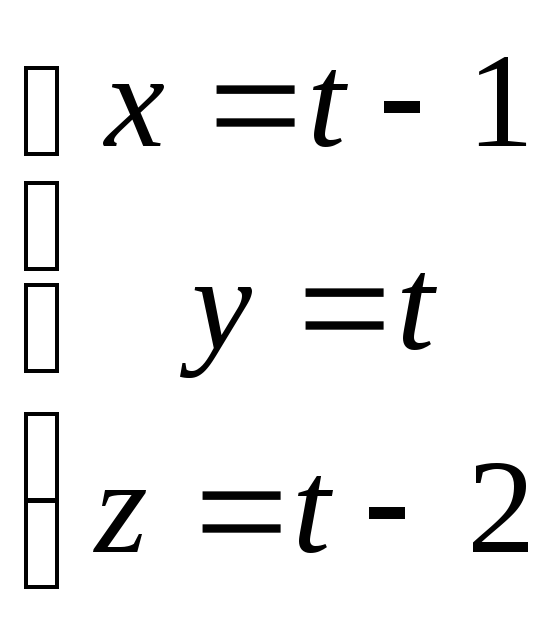
Видим, что вектор L (1,1,1) – направляющий прямой и точка М₀(-1,0,-2) лежит на прямой.

Находим = [, ]= = 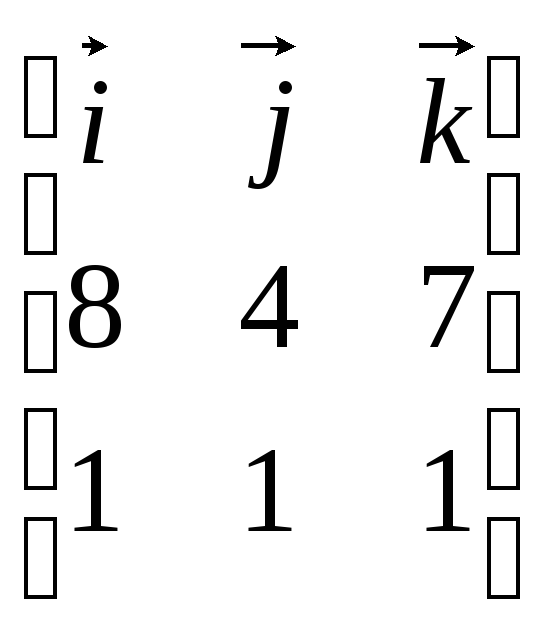4+7+8-4-7-8=-3-+4

Записываем уравнение плоскости

-3х-у+4z+d=0.

Точка М₀ лежит на плоскости, поэтому 3-8+d=0; d=5.

Уравнение плоскости имеет вид

-3х-у+4z+5=0 или –3х-у+4z=-5

уравнение плоскости в отрезках

++=1

следовательно длина отрезка, отсекаемого этой плоскостью от оси ординат равна У=5

Ответ: У = 5.

Задача №6.

Две прямые , пересекающиеся в точке Р(0,0,z₀); z₀>0 параллельна плоскости 2х+у+2z+6=0 b отстоят от неё на расстоянии 4. Одна из прямых пересекает ось абсцисс, а вторая- ось ординат. Найти тангенс острого угла между ними.

РЕШЕНИЕ.

Расстояние от точки Р до плоскости 2х+у+2z=0 можно вычислить по формуле:

d= ; d==4, =4,

2z₀+6=12, 2z₀=6, z₀=3; Р(0,0,3)

2z₀+6=12 2z₀=6 z₀=3; Р(0,0,3)

Обозначим точки пересечения осей координат через M и N. Тогда =(х,0,-3).

За нормаль плоскости проходящая через две пересекающиеся прямые можно взять нормаль =(2,1,2) заданной плоскости, так как они параллельны.

По условию   * =0  2х-6 = 0, х = 2;   * = 0  у-6 = 0

у = 6

Z

Найдём косинус угла между векторами Р(0,0,3)

= (х,0,-3), = (0,у,-3) N(0,у,0)

cos= == = 0 У

М(х,0,0)

1+tg²=  tg²⁼-1=10-1=9 Х

откуда tg=3 (т.к. угол острый, то корень tg=-3 не рассматриваем).

Ответ: tg=3

Задача №7.

Найдите радиус окружности с центром в точке М(2,4), если известно, что прямая 3х + 4у + 8 = 0 касается этой окружности.

РЕШЕНИЕ:

Радиус окружности найдём как расстояние от точки М до касательной прямой окружности по формуле.

R = =  ==6

ОТВЕТ: R = 6.

ЗАДАЧА № 8.

Дана кривая 25х² + 16у² – 150х – 32у - 159 = 0

8.1. Доказать, что эта кривая эллипс

25(х²- 6х +9 -9) + (у² – 2у +1 - 1) – 159 = 0

25(х-3)² – 225 +16(у – 1)² –16 –159 = 0

25(х-3)² + 16(у-1)² = 400

= 1 – уравнение эллипса.

8.2 Центр эллипса находится в точке (3,1)

8.3 Большая полуось b = 5, малая полуось a = 4. У

8.4 C===3,

- эксцентриситет эллипса

Уравнение фокальной оси у – 3 = 0.

1

0 33

3 Х

ЗАДАЧА № 9.

Дана кривая у² – 2у + 4х + 9 = 0

9.1 Доказать, что данная кривая – парабола.

(у – 1)² – 1 + 4х + 9 = 0, (у – 1)² = -4х-8, (у – 1)² = -4(х +2)

Если положить у₁ = у – 3, х₁ = х + 2, то уравнение приводится к виду

У₁² = - 4х, где 2р = - 4, р = 2.

9.2 координаты вершин (-2,1).

9.3 значение параметра р: р = -2.

9.4 ось симметрии: у – 1 = 0, у = 1. У

9.5 построим параболу:

1

-2 0 Х

ЗАДАЧА № 10.

Дана кривая х² – 7у² – 6ху + 2х + 26у + 57 = 0

10.1 Доказать, что кривая – гипербола

Приводим квадратичную форму В = х² – 7у² –6ху к главным

Её матрицу В = = - 7 -  + 7 + ² – 9 = ² + 6 - 16 = 0,  = -3 5.

Его корни ₁ = -8, ₂ = 2 являются собственными числами. Так как _{1 *} ₂ = -16 0, то кривая – гипербола, то координаты собственного вектора отвечающего числу ₁ = - 8 удовлетворяют соотношению , . Пологая найдём собственный единичный вектор; По свойству собственных векторов симметрического оператора второй вектор ортогонален вектору . Выберем вектор таким образом, чтобы базис был правым от старого базиса (0,,) перейдем к новому базису (0,,) .

Матрица перехода имеет вид

,

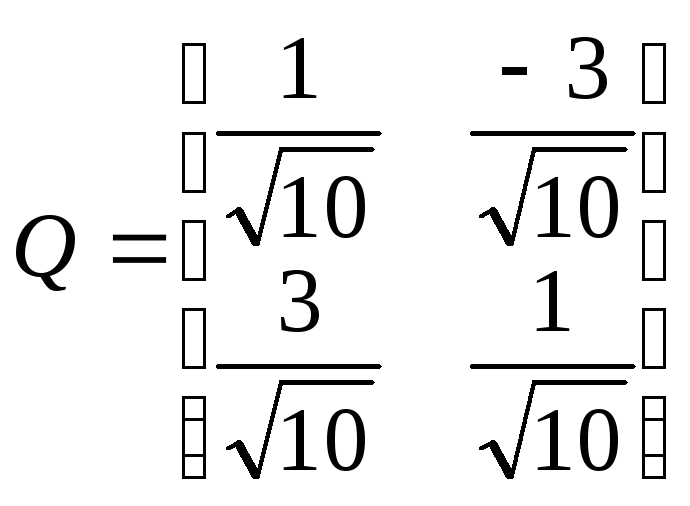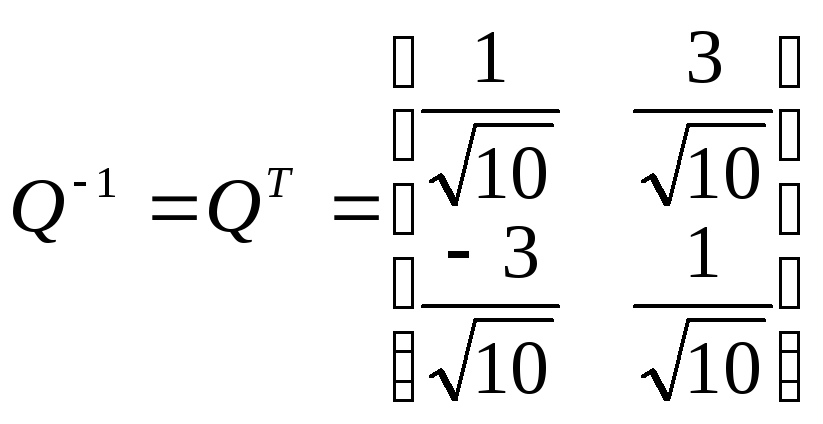
Старые координаты (х, у) связаны с новыми (х₁, у₁) соотношениями

 ,

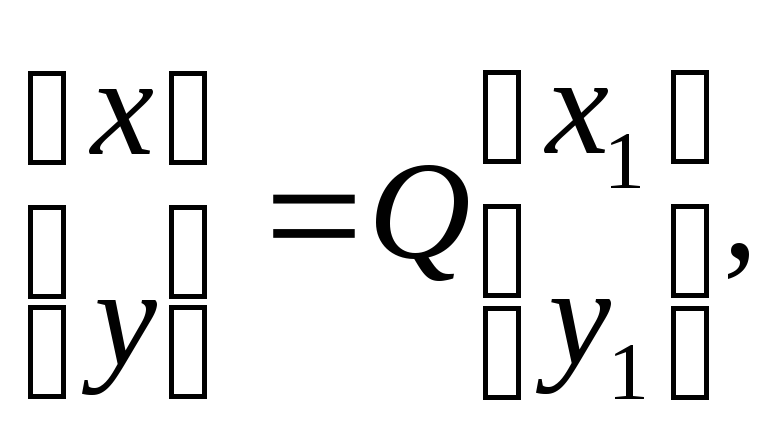
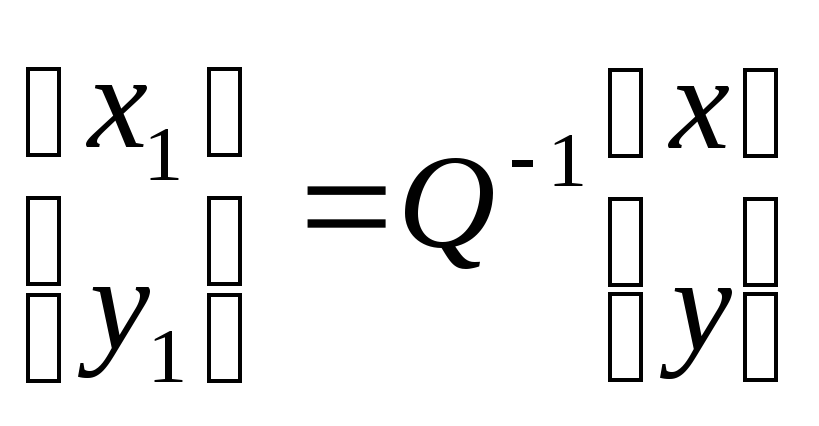
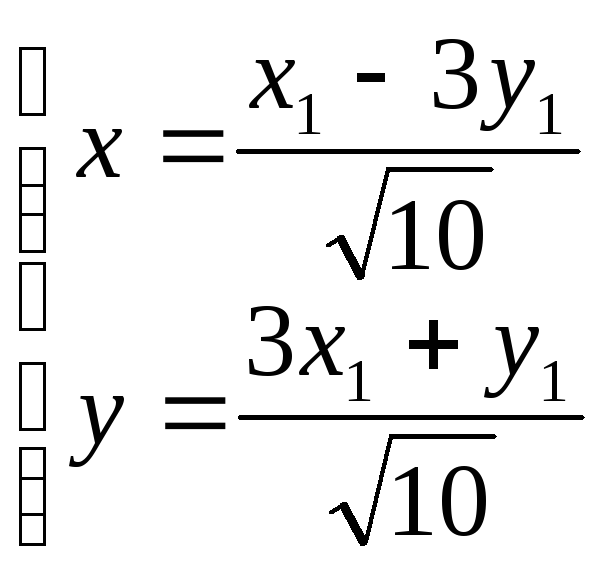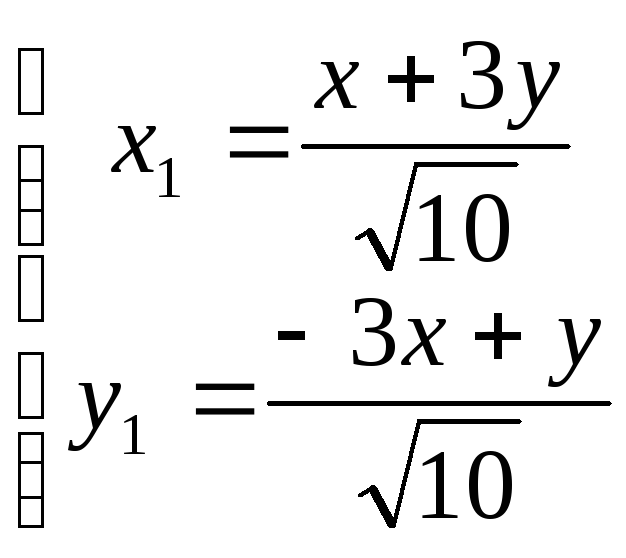
В новой системе координат уравнение данной кривой примет следующий вид:

*

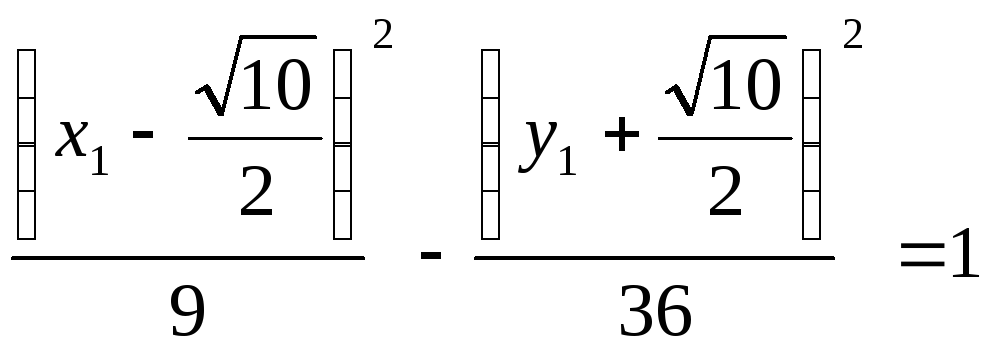
Видим, что действительная полуось а = 3, а мнимая b = 6.

Произведём преобразование параллельного переноса системы координат в новое начало 0₁ по формуле

, 

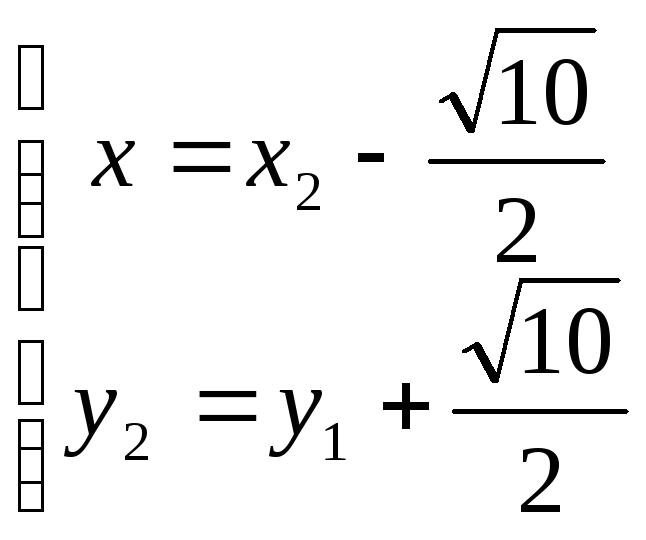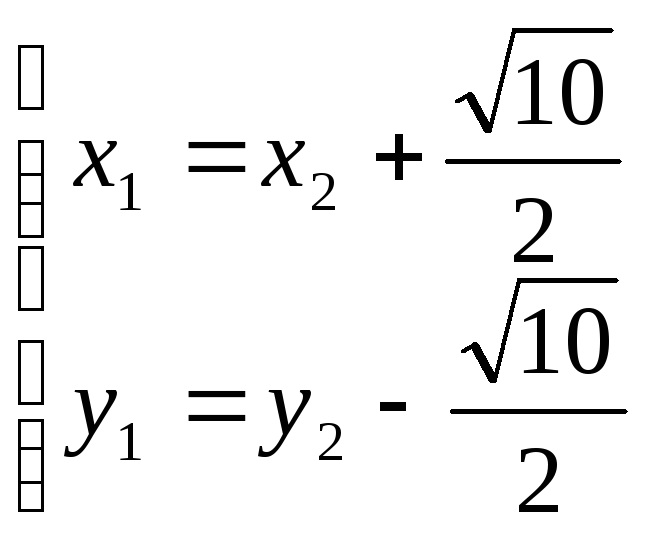
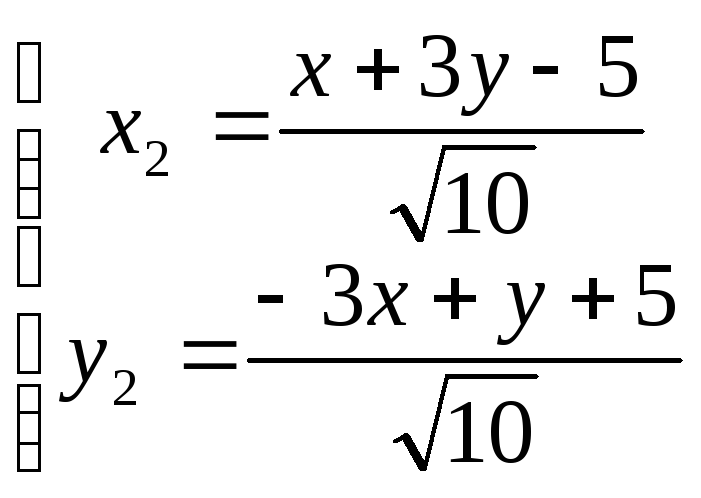
В системе координат (0₁, ) гипербола имеет уравнение

оси 0₁ х_2, 0₁ у₂ направлены по прямым х + 3у – 5 = 0, 3х – у – 5 = 0. Координаты точки 0₁, являющиеся центром симметрии гиперболы, найдём, решив систему:

 0₁(2,1).

Фокальной осью является прямая у₂ = 0, 3х – у – 5 = 0.

Прямые являются асимптотами гиперболы.

У У₁

0₁

0 Х

Х₁